Зразки розв’язування задач

Приклад 1. Знайти частинні похідні функції

Розв’язання.

Вважаючи сталим, дістанемо:

.

Вважаючи 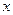сталим, дістанемо:

Приклад 2. Знайти частинні похідні другого порядку функції .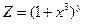

Розв’язання.

Знайдемо частинні похідні першого порядку:

;

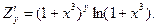
Диференціюємо повторно, дістанемо:

,

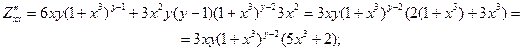
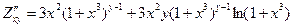або

Тобто, .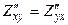

Приклад 3. (Задача 3.1) Перевірити, що функція задовольняє умові 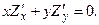Знайти частинні похідні.

Розв’язання.

Знайдемо частинні похідні:

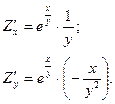
Отже,

Таким чином доведено, що функція задовольняє умові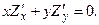

Знайдемо частинні похідні другого порядку:

;

;

.

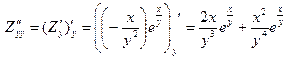Похідна за напрямом. Нехай функція визначена в деякому околі точки – вектор з початком в точці , – точка околу, що лежить на векторі 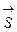, – приріст аргументу на промені 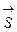. Якщо існує 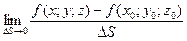, то ця границя називається похідною функції за напрямом вектора 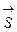у точці , тобто:

Похідна за напрямом характеризує швидкість зміни функції у точці за напрямом вектора .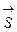

Якщо функція має в точці неперервні частинні похідні, то в цій точці існує похідна за напрямом вектора 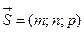, причому,

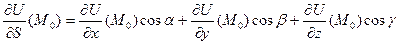, де

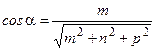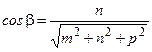; ; . (4.1)

Градієнтом функції називається вектор, координатами якого є значення частинних похідних функції в точці :

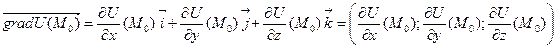, (4.2)

Градієнт функції в точці 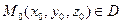характеризує напрямок та величину максимального зростання функції в точці .

Приклад (Задача 3.2). Для функції знайти градієнт в точці 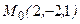і похідну в точці 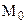за напрямом вектора 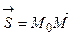, де .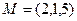

Розв’язання.

Знайдемо частинні похідні функції в точці :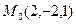

,

,

.

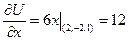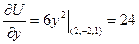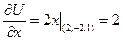За формулою 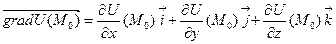дістанемо:

.

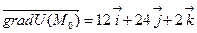Знайдемо похідну функції в точці за напрямом вектора .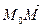

Знайдемо координати вектора 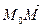та його напрямні косинуси:

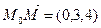, отже ;

; ; .

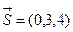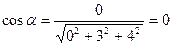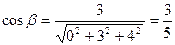За формулою 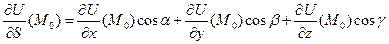дістанемо:

.

Екстремум функції двох змінних.

Функція має в точці локальний максимум (мінімум), якщо існує окіл точки 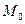, в якому при 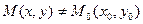виконується нерівність (відповідно , для всіх точок , що належать даному околу).

Точка 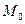називається точкою локального екстремуму функції .

Необхідна умова екстремуму. Якщо диференційована функція досягла екстремуму в точці 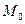, то в цій точці:

, (4.3)

або в цій точці частинні похідні не існують.

Точки, в яких виконуються ці умови називаються стаціонарним.

Достатні умови екстремуму. Нехай у стаціонарній точці 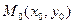, та в деякому околі цієї точки функція має неперервні частинні похідні другого порядку:

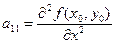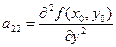; ; . (4.4)

Тоді:

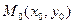1) має в точці максимум, якщо 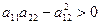та ; (4.5)

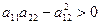2) має в точці мінімум, якщо та 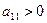; (4.6)

3) не має екстремуму, якщо ; (4.7)

4) Якщо 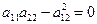, тоді екстремум в точці 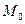може існувати, а може і не існувати, тобто в цьому випадку потрібні додаткові дослідження.

Приклад 4. Дослідити на екстремум функцію .

Розв’язання.

Знайдемо частинні похідні: ; .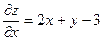

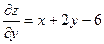Використаємо необхідну умову існування екстремуму:

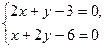
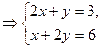звідки .

Точка − стаціонарна (в цій точці виконується необхідна умова).

Знайдемо значення других похідних у точці :

; ; ,

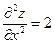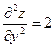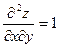тоді , , , отже 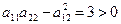. Оскільки 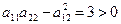і (за (4.6)), то в точці функція має мінімум .

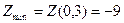Зауваження. З необхідними та достатніми умовами екстремуму функції багатьох змінних можна познайомитися у вказаній на початку параграфа літературі.

Приклад 5. (Задача 3.3). Нехай фірма випускає два види товарів. Позначимо їх обсяги через 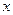і . Нехай ціни на ці товари відповідно 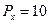, 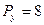ум. од., а функція витрат 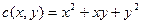. Знайти максимальний прибуток, який може одержати фірма.

Розв’язання.

Функція прибутку фірми: . Для цієї функції потрібно знайти екстремум. Знайдемо стаціонарні точки:

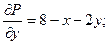
, отже стаціонарна точка .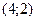

Перевіримо достатні умови локального екстремуму.

; ;

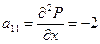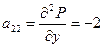Тоді 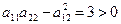, так як , то точка 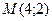− точка локального максимуму. Максимальний прибуток фірми: 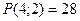ум. од. Таким чином максимальний прибуток фірма отримає при даному спектрі цін, що склалися на ринку, якщо буде випускати одиниці виду і 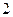одиниці виду товарів.

Метод найменших квадратів можливої лінійної залежності між змінними

На практиці, зокрема в прикладних питаннях економіки, часто виникає потреба знайти залежність між змінними на підставі проведених експериментів і спостережень.

Нехай потрібно визначити залежність між двома змінними 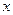і для яких із практичних досліджень відомо, що значення 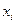відповідають значенням . Результати експерименту подано в таблиці:

	…
	…

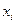
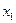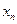
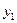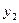Точки з координатами 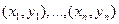на площині утворюють деяку лінію. Наприклад, виявилося, що точки групуються вздовж деякої прямої.

Тоді природно шукати аналітичну залежність у вигляді лінійної функції . Отже, задача зводиться до знаходження таких 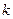і , щоб шукана пряма якнайточніше наближалася до всіх точок .

Для знаходження коефіцієнтів 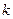і використовують метод найменших квадратів. Було доведено, що ці коефіцієнти можна знайти з системи рівнянь:

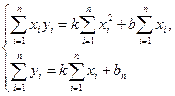(4.8)

Приклад 6. (Задача 3.4) Результати експерименту приведено в таблиці:

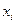
	-0,4	0,1	0,3	0,9	1,2	1,8

Методом найменших квадратів знайти параметри 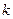і функції .

Розв’язання.

Побудуємо точки з координатами на координатній площині (Рис.6). Припустимо, що між ними існує лінійна залежність .

Рис. 6

Знайдемо 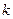і з системи (4.8):

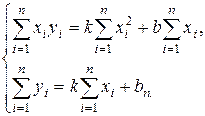
Обчислюємо:

;

;

;

.

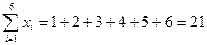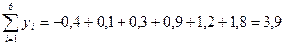Складемо систему:

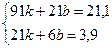
Розв’яжемо за формулами Крамера:

,

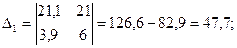
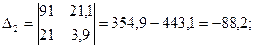
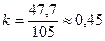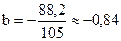
Таким чином, пряма, яку шукали, задається рівнянням .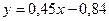

Дата добавления: 2014-11-29