Навигационная функция расстояния до ориентира на плоскости

Градиент навигационной функции - это вектор максимальной скорости изменения НФ в конкретной точке поля навигационных параметров, который направлен по нормали к навигационной изолинии в сторону увеличения НП.

НИ - это геометрическое место точек равных значений навигационных параметров.

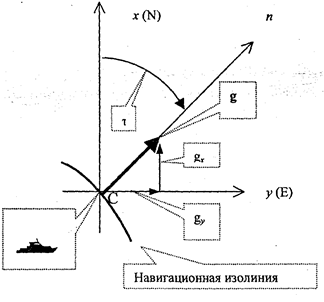
Важнейшей характеристикой навигационной функции (рис 1.1) является ее вектор-градиент g, который характеризует максимальную скорость изменения

навигационной функции (ско­рость изменения навигационного параметра в конкретной точке). НП меняется быстрее всего в направлении п, перпендикуляр­ном касательной к навигацион­ной изолинии в точке С. В дан­ном случае говорят, что градиент направлен по нормали п к НИ. В качестве положительного на­правления градиента g условно принимается направление, соот­ветствующее увеличению нави­гационного параметра U.

Для вычисления этой скоро­сти, т.е. модуля вектора градиен­та, необходимо вычислить про­изводную от НФ по нормали п:

Рис. 1.1. Градиент навигационной функции

Запишем формулы (1.5), (1.6) для расчета g (здесь g - обозначение вектора, а g -его модуля).

В локальной прямоугольной системе координат g может бьггь представлен в виде двухкомпонентного вектора следующим образом:

Тогда его модуль рассчитывается по теореме Пифагора:

здесь g^, gy - проекции вектора g на координатные оси. Направление вектора^ определится следующим образом:

Пояснение формул (1.3) - (1.7) представлено на рис. 1.1.

Рассмотрим измерения навигационного параметра D, которым является расстояние до навигационного ориентира А, измеряемое дальномерными навигационными приборами. Одним из таких приборов является радиолокационная станция (РЛС).

С учетом практической точности решения навигационных задач на земной сфере (см. книгу [2]), плоскость в качестве локальной модели земной поверхности можно использовать на расстояниях до 120 миль от ориентира.

На рис. 1.2 изображена нави­гационная функция расстояние D(x,y) в виде поля навигационные изолиний, которые представляют ш плоскости концентрические окруж­ности радиусом D и центром в точке расположения навигационного ори­ентира А. Эти окружности в морской навигации называются изостадиями.

Аналитическое выражение для навигационной функции на плос­кости с началом координат в точке А (рис. 1.3) запишем в традиционном виде:

а для вычисления модуля и направления градиента расстояния go в счислимой точке С воспользуемся формулами (1.5) - (1.7):

Результаты вычислений по фор­мулам (1.9) очевидны, что подтверж­дает их справедливость. Вычисли­тельная модель адекватна реальной ситуации. Выражение в квадратных скобках - не что иное, как счислимое расстояние dc от счислимой точки С до ориентира А. Модуль градиента расстояния без-размерен и направлен по линии пе-ленга П в сторону увеличения дис-танции D. При определении тд знак «+» принима­ется, если П< 180°, а знак «-», если

П>180°. Иллюс­трация век­

Рис. 1.3. Изолиния и градиент расстояния

торного поля градиентов навигационной функции D(x,y) представлена на рис. 1.4, из которого также видно, что перемещение по линии пеленга от ориентира, т.е. по нормали п к изостадии на величину An, равно такому же изменению расстояния AD до ориентира.

Рис. 1.4. Поле go

Дата добавления: 2014-11-29