Навигационная функция прямого и обратного пеленга на сфере

При пеленговании на сфере различают два случая:

1) с судна пеленгуется навигационный ориентир А, т.е. измеряется прямой пеленг П (обратная радиозасечка);

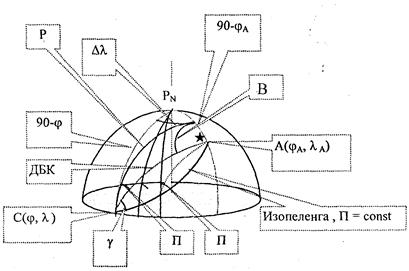
Т) с ориентира пе­ленгуется судно С, т.е. измеряется обратный пеленг В (прямая ра­диозасечка). В случае прямого пеленгования навига­ционного ориентира с судна на больших рас­стояниях навигацион­ная функция может быть получена средст­вами сферической три­гонометрии. На рис. 1.17 навигационный ориентир А пеленгу-

Рис, 1.17. Изолинии прямого и обратного пеленга на сфере

ется из точки С. Если необходимо двигаться так, чтобы навигационный параметр П на ориентир А всегда был постоянным, то нужно следовать по некоторой кривой, называемой изопеленгой, или изоазимутой. Эта кривая показана на рис. 1.17 яркой линией, в любой ее точке угол П между нордовой частью истинного меридиана и направлением на ориентир (дуга большого круга) будет постоянным.

Если судно запеленговано с помощью пеленгаторной станции, то изолинией постоянного пеленга В с ориентира на судно будет ДБК (ортодромия), которая по кратчайшему расстоянию соединяет точки А и С. Обе кривые в точке А и в точке С по-разному ориентированы относительно меридиана и эта разница фиксируется углом у, который называется сферическим схождением мвридианов.

В обоих случаях уравнение навигационных функций может быть получено из сферического треугольника РпАС по теореме котангенсов:

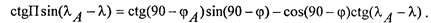
Для первого случая

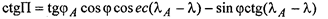
Для второго случая

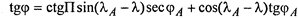
задаваясь в выражении (,1.^^; координатами навигационного ориентира, величиной ортодромического пеленга В и долготой судна, имеем возможность вычислять широту точек ортодромии.

Параметры градиентов можно получить используя традиционные приемы, показанные ранее. Приведем результаты, известные из литературы по навигации:

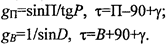
Здесь Р — сферический перпендикуляр, опущенный из точки С на меридиан точки A; D = AC - расстояние от точки А до точки С по ортодромии.

Дата добавления: 2014-11-29