
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Прямой аналитический расчет координат места судна
|
|
|
|
Для определения координат места судна на двумерной поверхности земного эллипсоида или шара необходимо измерить, как минимум, два навигационных параметра, и зная выражение навигационной функции, записать систему уравнений навигационных изолиний.
В качестве примера на судне можем измерить два навигационных параметра (расстояния) da и db до ориентиров а(\а,уа) и В(хд,уд). Используя систему уравнений навигационных функций (1.24) при условии, что da = 5, а db =10, система уравнений навигационных изолиний запишется в виде
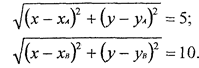
Теперь необходимо решить систему (1.37) относительно неизвестных координат (х,у), которые и являются координатами места судна.
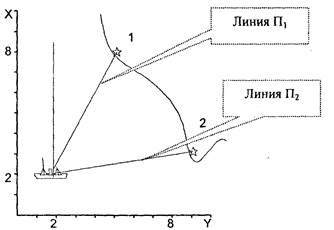
Прямое аналитическое решение таких задач имеет достаточно сложный вид даже для простых навигационных функций. Рассмотрим задачу определения места по двум пеленгам на плоскости.
Система уравнений, записанная из выражения (1.10), в соответствии с рис. 1.19, будет иметь вид:
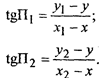
где xi,Х2, у), уз - координаты навигационных ориентиров.
Обозначив tglli через Т\, a tgllz через Тз (хо =х, уо =у), запишем алгоритм решения системы:
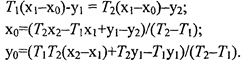
Пусть П) = 30°, Пз = 82°, xi = 8, yi = 5, xz= 3, y-i = 9. Тогда обсервованные
прямоугольные координаты рассчитаем следующим образом:
хо = (tg(820)•3-tg(300)•8+5-9)/(tg(820)-tg(300) = 1,95 мили;
уо = (tg(300)•tg(820)•(3-8)+(tg(820)•5-(tg(300)•9)/(tg(820)-tg(300) = 1,50 мили. Подобные решения существуют и при определении места судна другими -способами: по двум расстояниям, двум горизонтальным углам, двум высотам светил
(задача Гаусса) и т.д.
| Прямые аналитические методы расчета координат имеют ряд недостатков: практически все навигационные функции являются нелинейными, а поэтому решение таких систем уравнений неоднозначно, что может привести к возникновению опасной ситуации. Поскольку методы решения не универсальны, это не дает единого подхода к синтезированию алгоритмов и программного обеспечения. |
|
| Рис. 1.19. Измерение двух навигационных параметров |
На основании вышеизложенного видно, что все навигационные функции на сфере описываются с помощью тригонометрических функций, которые, в силу своей периодичности, вносят дополнительную многозначность в расчет координат.
На пра-ктике прямой аналитический метод заменяют графоаналитическим подходом, т.е. навигационные изолинии прокладывают или заранее наносят на навигационной карте.
Линейные методы расчета координат места судна
Глава содержит описание методов обработки навигационной информации и оценки точности обсервации.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 1475; Нарушение авторских прав?; Мы поможем в написании вашей работы!