Равноточные измерения

Число навигационных измерений при определении места судна очень существенно. Если измеряются два навигационных параметра и определяются две координаты, то говорят, что в задаче отсутствует избыточность, т.е. система уравнений (2.6), как правило, совместна.

Отсутствие избыточности измерений приводит к неконтролируемому влиянию различных видов погрешностей на результат, особенно опасны грубые промахи и систематические погрешности.

Для получения более надежной обсервации применяют избыточные навигационные измерения.

Пусть для определения координат измерены три навигационных параметра (п = 3), а определить нужно две координаты (k = 2). В этой ситуации избыточность r = n-k= 1.

Первоначально систему уравнений линий положения в матричном виде запишем так же, как систему уравнений (2.6):

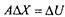
однако матрицы будут иметь вид:

В данной системе количество неизвестных k меньше, чем количество уравнений п. Решение любых двух уравнений дает положение одной из вершин треугольника. Это означает, что подстановка этого решения в третье уравнение, не обратит его в тождеств \ Такая система называется несовместной, т.е. решение пары уравнений не совместно с третьим. Для получения согласованного решения системы необходимо ввести дополнительные условия. Если предположить, что систе­

матические погрешности в изме­рениях отсутствуют, т.е. они определены и исключены специ­альными приемами измерений, то все остальные погрешности изме­рений можно считать случайными. Известно, что центром группиро­вания случайных величин явля­ется их математическое ожидание или его оценка - среднее зна­чение, которое наиболее близко к истинному значению и имеет ми­нимальную дисперсию. Очевидно, что и в данном случае необходимо

Рис. 2.2. К выводу формулы решения системы уравнений (2.7)

найти некоторое среднее из трех точек, которое будет иметь статус оценки математического ожидания множества, состоящего из трех измерений. Ясно, что эта точка должна быть в фигуре погрешностей, а не вне ее. Несогласованность измерений возникает из-за погрешностей, которые называют невязками системы уравнений.

Теперь вместо системы (2.9), с учетом невязок, более корректно следует записать следующее матричное уравнение (система уравнений поправок):

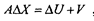
где V- вектор невязок (погрешностей), который имеет вид:

Если принять, что для получения согласованного решения линии положения необходимо сдвинуть внутрь фигуры погрешностей на некоторые величины v/, v^ и уз соответственно (рис. 2.2), то математическое условие поиска оптимального согласованного решения относительно этого среднего значения (точка О) определится в соответствии с формулой (2.11), т.е. минимальной длиной вектора V:

здесь величины v\, v-г. и уз, выраженные в единицах измерений, называются невяз­

ками, поправками или погрешностями измерений в за­висимости от при­даваемого им знака. Выражение (2.11) определяет усло­вие решения сис­темы (2.10), а от­сюда и название рассматриваемого метода — метод наименьших квад­ратов.

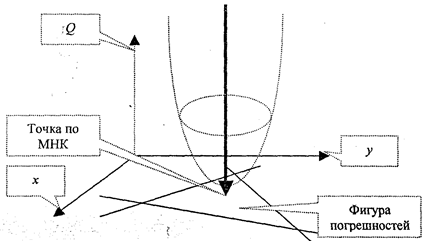
Рис. 2.3. Геометрическая интерпретация МНК

Из формулы (2.10) запишем выражение относительно вектора невязок:

Взяв производную от выражения (2.12) по вектору неизвестных и приравняв ее к нулю, находим формулу для решения системы (2.10):

Система (2.13) называется системой нормальных уравнений. Теперь можно записать решение:

Знак «^л» над вектором искомых величин свидетельствует о том, что решение получено с применением критерия оптимальности Q, Рис. 2.3 поясняет решение по МНК.

После получения решения, согласно выражению (2.14) относительно счислимой точки в локальной системе координат, используется формула (2.8), а затем вьшолняется итерационная процедура. Точка, положение которой определяется вектором Хо, называется ввроятнвйшвй точкой.

Дата добавления: 2014-11-29