Седиментаційний аналіз суспензії

ЛАБОРАТОРНА РОБОТА

САМОСТІЙНА РОБОТА НА ЗАНЯТТІ

ІІ. Дати письмові відповіді на контрольні запитання

І. Засвоїти основний матеріал навчальної програми

ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ ПОЗААУДИТОРНОЇ РОБОТИ

1. Класифікація грубодисперсних систем.

2. Властивості аерозолів і порошків. Використання у медицині і фармації.

3. Емульсії. Їх класифікація. Властивості і застосування.

4. Характеристика пін. Типи пін. Використання.

5. Суспензії. Їх класифікація. Властивості і застосування.

6. Ступінь дисперсності та полідисперсності.

7. Основи седиментаційного аналізу і його завдання.

8. Колоїдні ПАР та їх класифікація.

9. Причини міцелоутворення у розчинних ПАР. Критична концентрація міцелоутворення (ККМ).

10. Солюбілізація і її застосування у фармації?

1. Які переваги аерозольної лікарської форми?

2. Порівняйте кінетичну та агрегатну стійкість суспензій з відповідними характеристиками ліофобних колоїдів.

3. Що називається ступенем дисперсності системи?

4. Приведіть графіки осідання для моно-, бі- та полідисперсної системи і поясніть хід цих кривих.

5. Що є метою седиментаційного аналізу?

6. Дайте формулювання законів Стокса та Архімеда

7. Як визначити ККМ у колоїдних ПАР?

1. Виконання тестових завдань.

2. Виконання лабораторної роботи.

3. Обговорення висновків та оформлення протоколу.

4. Захист протоколу.

Інформаційна частина

У мікрогетерогенних системах, позбавлених броунівського руху, частинки дисперсної фази осідають або спливають (якщо ρ < ρ₀).

Якщо рух потоку частинок в рідкому або газоподібному середовищі ламінарний і може бути описаний рівнянням Стокса, то вимірювання швидкості осідання (спливання) частинок дає можливість визначити розмір частинок. На сферичну частинку з радіусом r і густиною ρ, що вільно осідає в дисперсійному середовищі, густина якого ρ ₀ і в'язкість η, діє сила тяжіння f яка дорівнює власній вазі частинки:

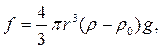(2.12)

де g – прискорення сили тяжіння.

Під впливом сили тяжіння частинка у в'язкому середовищі рухається рівномірно-прискорено. Водночас із силою тяжіння на частинку діє сила опору середовища F, яка за законом Стокса дорівнює:

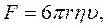(2.13)

де υ – швидкість седиментації; η – в'язкість середовища.

Спочатку частинка рухається прискорено, бо при малих швидкостях сила тяжіння перевищує силу тертя. При збільшенні швидкості руху сила тертя зростає і в деякий момент урівноважує силу тяжіння, внаслідок чого частинка починає рухатися із сталою швидкістю:

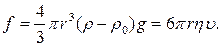(2.14)

З рівняння (2.14) знаходимо швидкість седиментації:

(2.15)

Отже, швидкість сферичної частинки, яка вільно рухається під впливом сили тяжіння, прямо пропорційна квадрату її радіуса і обернено пропорційна в'язкості дисперсійного середовища. Швидкість руху частинки можна знайти з відношення шляху h до часу τ, за який цей шлях був пройдений, і, підставивши дані в рівняння (2.15), обчислити радіус частинки:

(2.16)

Якщо в рівнянні (2.16) величина

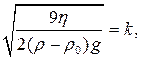
тобто є величиною сталою для даної системи і умов досліду, то

(2.17)

Рівняння (2.17) вірне для частинок з розміром 10^–7–10^–4 м.

На практиці дисперсну систему характеризують розподілом частинок за розмірами і фракціями (вміст дисперсної фази в заданих інтервалах радіусів частинок). Такий аналіз полідисперсності одержав назву седиментаційного аналізу.

Він складається з одержання кривої седиментації, тобто залежності маси осаду m дисперсної фази, яка осіла до певного часу, від часу осадження τ. Для монодисперсної системи (з частинками одного розміру) така залежність є лінійною:

де Q – загальна маса дисперсної фази; H – початкова висота стовпа дисперсної системи.

Усі реальні дисперсні системи полідисперсні (частинки дисперсної фази мають різні розміри), і тому швидкість осідання різна для різних фракцій: крупні частинки осідають швидше, малі – повільніше. Тому крива седиментації вигнута до осі ординат (рис 2.7, 2.8).

Тангенси кута нахилу дотичних в даних точках кривої седиментації визначають швидкості седиментації відповідних фракцій частинок. Знаючи швидкість осадження частинок окремих фракцій, за рівнянням (2.17) можна розрахувати їх розміри (радіуси). Загальна кількість дисперсної фази, яка осіла до довільного моменту часу τ ₁, виразиться рівнянням

(2.18)

τ1 τ
Рис. 2.7. Крива седиментації монодисперсної системи	Рис. 2.8. Крива сидементації полідисперсної системи

Величина Q ₁ визначається відрізком, який відсікається на осі ординат дотичною до кривої седиментації в точці τ ₁, і характеризує масу частинок у фракції, які повністю випали в осад до моменту часу τ ₁. Оскільки радіус частинок, які пройшли за час τ ₁ усю висоту стовпа Н дисперсної системи, то Q ₁ – це маса частинок системи з r ≥ r ₁. Член (dm/d τ) τ ₁ характеризує масу частинок з r ≤ r ₁, які осіли до моменту часу τ ₁. Як правило, визначають відносну масу частинок дисперсної фази, які осіли (в % від загального вмісту дисперсної фази в системі). В цьому випадку m_найб = 100%, а величини Q ₁ і Q₂ є процентними вмістами фракцій з радіусом відповідно r ≥ r ₁, r ≥ r ₂ і так далі. Таким чином, можна побудувати інтегральну криву розподілу частинок за їх розмірами – залежність Q % від r. Загальний вигляд кривої зображений на рис. 2.9, а.

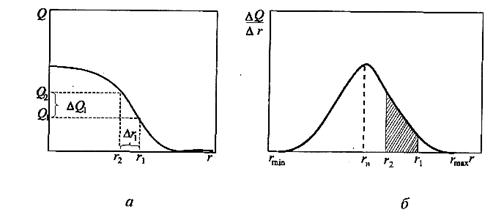
Рис. 2.9. Інтегральна (а) і диференційна (б) криві розподілу частинок за радіусом

Інтегральна крива дозволяє визначити процентний вміст фракцій. Наприклад, для фракції, яка містить частинки розміром від r₁ до r₂, вона дорівнює Δ Q ₁ = Q ₂ – Q ₁.

Більш наочне представлення про розподіл частинок в дисперсній системі за розмірами дає диференційна крива розподілу, яка є залежністю Δ Q /Δ r (в межі d Q /d r) від радіусу частинок r (рис. 2.9, б).

Для її побудови можна використати інтегральну криву, визначаючи збільшення Δ Q для серії фракцій Δ r, або криву седиментації, визначаючи Δ Q як відрізки, що відсікаються сусідніми дотичними на осі ординат, наприклад, ΔQ₁ = Q₂ – Q₁. Для знаходження Δ r = r ₂ – r ₁ необхідно визначити радіус частинок, які осіли до моменту часу τ ₁ і τ ₂. Максимум на диференційній кривій відповідає найбільш характерному для системи радіусу частинок. Щоб знайти за кривою розподілу процентний вміст частинок з радіусом від r ₁ до r ₂, треба взяти відношення площі, заштрихованої на рисунку, до площі під усією кривою і помножити на 100.

Для проведення седиментаційного аналізу полідисперсних систем використовують різного типу седиментометри. У седиментометрі Фігуровського (рис. 2.10) до пружного скляного або кварцового плеча прикріплена на скляній нитці з крючком чашечка, на якій накопичується осад.

Рис. 2.10. Седиментатор Фігуровського

Прогин плеча вимірюють за шкалою при допомозі мікроскопа. По мірі осідання частинок дисперсної фази прогин плеча збільшується спочатку швидко, внаслідок переважного випадання найбільш важких частинок, а потім все повільніше, включно майже до повного осідання. Визначаючи зміщення кінця нитки вниз по вертикалі і відмічаючи час спостереження, одержують криву седиментації. Такий метод дуже простий, доступний і дає хороші результати.

При дисперсному аналізі високодисперсних систем або систем з малою різницею густини частинок дисперсної фази і дисперсійного середовища седиментацію проводять у відцентровому полі з використанням центрифуги.

Дата добавления: 2014-11-29