Загальний вигляд матриці ризиків

Вигляд платіжної матриці для випадку ігор із природою

А\П	П1	П2	…	Пm
А1	α	α	…	α
А2	α	α	…	α
.	.	.	…	.
Аm	α	α	…	α

Потрібно вибрати оптимальну стратегію гравця А.

Зауважимо, що, на відміну від класичної теорії ігор, виграші гравця А вже не можуть тлумачитися як програші природи, тому що природа є безликою субстанцією і для неї не існує виграшів і програшів.

Ця задача складніша, ніж у теорії ігор, оскільки щодо поведінки природи не можна зробити ніяких припущень. Вона не може знати наших планів і свідомо протидіяти їм, оскільки нерозумна і незловмисна. Здавалося б, за таких обставин легше робити вибір, однак це не так: при розв’язуванні оптимізаційної задачі не існує критерію для вибору поведінки природи. Тому вводиться показник ризику, який описує «вдалість» застосування гравцем А тієї чи іншої стратегії з урахуванням стану природи.

Ризиком r_ij при стратегії А в умовах П називається різниця між виграшем, який міг би бути отриманий в оптимальному випадку, і виграшем, який отримується насправді:

r_ij = β_j - α_ij

де, β_j = max α_ij (максимальне значення в колонці j), тобто виграш А в оптимальному варіанті.

Платіжній матриці ставиться у відповідність матриця ризиків (табл. 5.2). Вона має той самий вигляд, що і платіжна матриця але її елементами є не виграші, а ризики.

Таблиця 5.2

A\B	П1	П2	…	Пn
А1	r11	r11	…	r1n
А2	r21	r21	…	r2n
.	.	.	…	.
Аm	rm1	rm2	…	rmn

У теоріях корисності Бернуллі та Джевонса людина ухвалює рішення в ізоляції, не маючи уявлення, та і не цікавлячись тим, що роблять інші. У теорії ігор вже не ізольована людина, а двоє або більш за людей прагнуть максимізувати свої вигоди одночасно, знаючи про цілі, вигоди і можливі дії інших.

Теорія ігор показала, що дійсним джерелом невизначеності є наміри інших. З цієї точки зору майже всяке схвалюване нами рішення є результатом ряду переговорів, в яких ми прагнемо понизити невизначеність, даючи іншим те, що вони хочуть, в обмін на те, чого хочемо ми. Вибір альтернативи, що обіцяє найбільшу вигоду, як правило, створює найбільший ризик, тому що він може спровокувати посилений захист з боку гравців, які в результаті наших зусиль повинні програти. Тому ми зазвичай вибираємо компромісні альтернативи, які можуть спонукати нас укласти кращу з гірших операцій; для опису таких рішень теорія ігор використовує терміни «максимінні» і «мінімаксні» рішення.

З огляду на відсутність «розумності» у поведінці супротивника для вибору кращої стратегії розроблені спеціальні критерії. На сьогодні їх відомо більше десяти. Ми розглянемо чотири основні.

1. Критерій Байєса-Лапласа

Цей критерій базується на припущенні, що відомо ймовірності станів природи:

q₁ = p (П₁), q₂ = p (П₂), … q_n = p(П_n), =1

Оптимальною вибирається та зі стратегій гравця А, для якої середнє значення або математичне сподівання виграшу перетворюється на максимум:

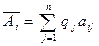
Цей критерій може тлумачитися як критерій з частковою невизначеністю, через те що ймовірності станів природи відомі.

Звернемо увагу на обов’язкову вимогу:

Вона означає, що використано всі можливі стани природи й інших бути не може.

2. Максимінний критерій Вальда

Оптимальною вибирається та зі стратегій гравця А, за якої мінімальний виграш є максимальним:

W = 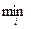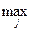α_ij.

Це критерій крайнього песимізму, що рекомендує діяти за принципом: «завжди розраховуй на гірше». Слід зазначити, що критерій Вальда має ту перевагу, що він надзвичайно консервативний, тобто безризиковий у такій ситуації, де недоцільно ризикувати.

3. Мінімаксний критерій Севіджа

Відповідно до цього критерію рекомендується обирати ту стратегію, за якої величина ризику набуває найменшого значення в найбільш несприятливій ситуації:

S = 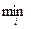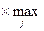r_ij

Це також критерій крайнього песимізму, але песимізм тут розуміється інакше: гіршим оголошується не мінімальний виграш, а максимальний ризик.

Критерії Вальда та Севіджа песимістичні в тому сенсі, що з кожним рішенням вони поєднують стан середовища, яке приводить до гарантованих (безризикових) наслідків для прийнятого суб’єктом керування рішення. Для моделювання поведінки середовища, що вважається найкращим для суб’єкта керування Гурвіц запропонував використовувати зважену комбінацію найкращого та найгіршого.

Такий підхід до вибору рішень відомий як критерій показника песимізму-оптимізму. Особливістю цього критерію є те, що в ньому передбачається не повний антагонізм середовища, а лише частковий.

4. Критерій песимізму-оптимізму Гурвіца

Цей критерій рекомендує в умовах невизначеності не керуватися ні крайнім песимізмом, ні крайнім оптимізмом, а брати щось середнє, і має вигляд:

H = max(χ minα_ij +(1-χ)maxα_ij),

де 0 < χ < 1 - коефіцієнт, який вибирається із суб’єктивних міркувань: чим небезпечніша ситуація, тобто чим більше сторона А бажає «підстрахуватися», тим ближче до одиниці слід вибирати х- Розглянемо докладніше цей критерій.

При χ = 1 — Н = 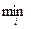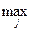це критерій Вальда.

При χ = 0 — Н = 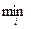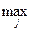позиція крайнього оптимізму.

При 0 < χ < 1 — щось середнє, залежне від того, чому віддає перевагу ОПР.

Таким чином, х відображає міру песимізму особи, яка приймає рішення, чи міру її ставлення до ризику.

Конкретні значення х має задавати ОПР. Незважаючи на те, що вибір χ суб’єктивний і немає ніяких конкретних рекомендацій щодо його вибору, в реальних умовах буває корисно переглянути при різних χ рекомендації, що випливають із критерію Гурвіца і зробити висновок щодо діяльності в умовах, які розглядаються.

Якщо рекомендації, що випливають із різних критеріїв, збігаються, можна не сумніватися у виборі рішення. Якщо не збігаються - слід замислитися над ситуацією.

Методи iмiтацiйного моделювання дістали широке застосування в економiцi. Слід відмітити, що як і в методі аналізу чутливості ризику, тут також здійснюється оцінка коливань результуючого показника за випадкових змін вхідних величин, але детальніше, з урахуванням ступеня взаємозалежності вхідних величин.

Узагальнюючи матеріали, наведені в низці літературних джерел, процес кiлькiсного аналізу ризику за допомогою методів iмiтацiйного моделювання можна розділити на сiм кроків.

Перший крок аналізу полягає у формуванні моделі об’єкта (проекту), що розглядається.

Другий крок здійснюється для визначення ключових аргументів (чинників ризику). Для подальшого аналізу ризику залишаються лише тi чинники, якi не є строго детермiнованими, а еластичнiсть вiдповiдної функцiї по даному чиннику (аргументу) є значною (суттєвою).

Третiй крок полягає у тому, щоб визначити можливi iнтервали вiдхилень прогнозованих значень параметрiв (чинникiв ризику) вiд очікуваних. На цьому етапі доречно використовувати математичнi (статистичнi) оцiнки якостi прогнозiв.

Четвертий крок полягає у визначеннi розподiлу ймовірності випадкових значень аргументiв (чинникiв ризику). Вiн здiйснюється паралельно з третім кроком.

П’ятий крок призначений для виявлення залежності, яка на практицi може iснувати мiж ключовими аргументами (чинниками ризику). Вважають, що двi і бiльше випадкові змiнні корельованi у тому разі, коли вони змiнюються систематично.

Слід зазначити, що ігнорування кореляцiї може призвести до неправильних результатiв в аналiзi ризику, тому важливо переконатися в наявностi чи вiдсутностi таких взаємозв’язкiв i, де це необхiдно, ввести при моделюваннi обмеження, якi знизили б до рацiонального рiвня ймовiрнiсть вироблення сценарiїв, що порушують вплив кореляцiї (взаємозалежностi).

Шостий крок полягає у здiйсненні генерацiї випадкових сценарiїв відповідно до системи прийнятих гiпотез щодо чинникiв ризику та згiдно з обраною на першому кроцi моделлю. Пiсля того, як всi гiпотези і вiдповiднi залежностi були ретельно дослiдженi, послiдовно здiйснюють обчислення згiдно з побудованою моделлю до тих пiр, доки не буде одержанa репрезентативна вибiрка можливих значень ключових аргументiв. Для цього, як свiдчить досвiд, достатньо, щоб вибiрка була одержана в результатi здiйснення 200-500 обчислень.

Сьомий крок. Пiсля серiї обчислень можна одержати розподіл частот для підсумкового показника (ефективностi, чистої теперiшньої вартостi проекту, норми доходу тощо). Результати можуть бути подані як дискретним, так і неперервним законом розподiлу результуючого показника як випадкової величини. Для перевiрки гiпотез про вид закону розподiлу можна застосувати відповідні статистичні критерії. Можна також обчислити числовi характеристики результуючого показника: математичне сподівання, дисперсiю, семіварiацiю, асиметрiю, ексцес тощо. Слід наголосити, що отриманi результати вимагають їхньої iнтерпретацiї.

Основними методами, які використовуються при імітаційному моделюванні є: аналітичний метод, метод статичного моделювання і комбінований метод (аналітико-статистичний) метод.

Аналітичний метод в більшості випадків використовується для імітації процесів для малих і простих систем, коли відсутній чинник випадковості. Наприклад, коли процес їх функціонування описаний диференційними або інтегродиференційними рівняннями. Метод названий умовно, оскільки він об’єднує можливості імітації процесу, модель якого отримана у вигляді аналітично замкнутого рішення, або рішення, отриманого методами обчислювальної математики.

Метод статистичного моделювання спочатку розвивався як метод статистичних випробувань (Монте-Карло). Це – чисельний метод, що полягає в здобутті оцінок імовірнісних характеристик, які співпадають з аналітичних завдань (наприклад, з вирішенням і обчисленням визначеного інтеграла). Надалі цей метод став застосовуватися для імітації процесів, що відбуваються в системах, усередині яких є джерело випадковості або які здатні до випадкових дій. Метод отримав назву методу статистичного моделювання.

Комбінований метод (аналітико-статистичний) дозволяє об’єднати переваги аналітичного і статистичного методів моделювання. Він застосовується в разі розробки моделі, що складається з різних модулів, які представляють набір статистичних та аналітичних моделей, і взаємодіють як єдине ціле.

Для оцінки стратегій пов’язаних із ризиком як правило застосовують метод Монте-Карло. Методи Монте-Карло – це загальна назва групи методів для розв’язання різних задач за допомогою випадкових послідовностей. Ці методи (як і вся теорія ймовірностей) виникли завдяки спробам людей поліпшити свої шанси в азартній грі. Цим пояснюється і той факт, що назву цій групі методів дало місто Монте-Карло – столиця європейського грального бізнесу.

Метод Монте-Карло – це сукупність формальних процедур, засобами яких відтворюються на ЕОМ будь-які випадкові фактори (випадкові події, випадкові величини з довільним розподілом, випадкові вектори тощо). У межах цього підходу будується ймовірнісна модель, яка відповідає математичній чи фізичній задачі, і на ній реалізується випадкова вибірка.

Метод Монте-Карло являє собою метод імітації для приблизного відтворення реальних явищ, моделювання результатів функціонування складної системи, на яку впливають випадкові фактори і яка, як правило, не може бути описана жодними іншими методами. Він об’єднує аналіз чутливості (сприйнятливості) і аналіз розподілювання ймовірностей вхідних змінних. Цей метод дає змогу побудувати модель, мінімізуючи дані, а також максимізувати значення даних, які використовуються в моделі.

Застосування даного методу створює додаткову можливість для аналізу та оцінки ризику за рахунок того, що робить можливою побудову випадкових сценаріїв. Застосування аналізу ризику використовує багатство інформації, будь вона у формі об’єктивних даних або оцінок експертів, для кількісного опису невизначеності, існуючої відносно основних змінних проекту і для обґрунтованих розрахунків можливої дії невизначеності на ефективність інвестиційного проекту. В загальному випадку метод імітаційного моделювання Монте-Карло є процедурою, за допомогою якої математична модель визначення якого-небудь фінансового показника піддається ряду імітаційних прогнозів на комп’ютері: будуються послідовні сценарії з використанням початкових даних; останні за задумом проекту є невизначеними і тому в процесі аналізу вважаються випадковими величинами. Процес імітації здійснюється так, щоб випадковий вибір значень з певних розподілів вірогідності не порушував існування відомих або передбачуваних відносин кореляції серед змінних. Результати імітації збираються та аналізуються статистично з тим, щоб оцінити міру ризику.

Алгоритм методу імітації Монте-Карло

Крок 1. Спираючись на використання статистичного пакету, випадковим чином вибираємо, базуючись на ймовірнісній функції розподілу, значення змінної, яка є одним із параметрів визначення потоку готівки.

Крок 2. Вибране значення випадкової величини поряд зі значеннями змінних, які є екзогенними змінними, використовується при підрахунку чистої приведеної вартості проекту.

Рис. 5.1. Схема роботи з моделлю

Кроки 1 і 2 повторюються багато разів, наприклад 1000, і отримані 1000 значень чистої приведеної вартості проекту використовуються для побудови щільності розподілу величини чистої приведеної вартості зі своїм власним математичним сподіванням і стандартним відхиленням.

Використовуючи значення математичного сподівання і стандартного відхилення, можна обчислити коефіцієнт варіації чистої приведеної вартості проекту і потім оцінити індивідуальний ризик проекту.

Тепер необхідно визначити мінімальне і максимальне значення критичної змінної, а для змінної з покроковим розподілом, крім цих двох значень, ще й інші значення, що приймаються нею. Межі варіювання змінною визначаються, просто виходячи зі всього спектра можливих значень.

За допомогою попередніх спостережень за змінною можна встановити частоту, з якою та набуває відповідних значень. У цьому випадку ймовірнісний розподіл є частотним, що показує частоту появи значень, щоправда, у відносному масштабі (від 0 до 1). Ймовірнісний розподіл регулює ймовірність вибору значень із певного інтервалу. Відповідно до заданого розподілу модель оцінки ризиків буде вибирати довільні значення змінної. До розгляду ризиків ми мали на увазі, що змінна набуває одного визначеного нами значення з імовірністю 1.1 через єдину ітерацію розрахунків ми отримували однозначно певний результат. У рамках моделі ймовірнісного аналізу ризиків проводиться велике число ітерпретацій, що дозволяють встановити, як поводиться результативний показник (в яких межах коливається, як розподілений) під час зміни в моделі різних значень змінної відповідно до заданого розподілу.

Даний метод простий та практичний в застосуванні. Тому доцільно більш детальніше зупинитися на практичному застосуванні даного методу. В практиці метод Монте-Карло реалізований у вигляді надбудови до Microsoft Ecxel. Розглянемо даний алгоритм наочно.

Для використання датчиків випадкових чисел потрібно підключити надбудову MCFunction.xla через меню Сервис\Надстройки…

Після цього в меню «Вставка функций» з’явиться нова група функцій «Monte-Carlo». Ці функції автоматично видають новий результат при кожному оновленні аркуша, тобто при кожному перерахуванні формул. Штучно оновлення можна викликати натисканням кнопки F9. Крім цього, так як перше значення датчика залежить від часу виклику функції, на різних комп’ютерах і в різний час датчики будуть видавати різні значення.

Далі більш детальна інформація та ілюстрації, отримані за допомогою надбудови «Моделювання Монте-Карло».

= Fmc_Rand (..). Повертає випадкове число з рівномірним розподілом від 0 до 1. Цей датчик не має параметрів і є вихідним для всіх інших датчиків де з його допомогою досягається більш складний розподіл. Тому він і працює швидше всіх інших. Звертайте увагу на швидкість роботи датчиків і інших функцій при моделюванні. Надбудова «Монте-Карло» завжди показує час розрахунку – на нього слід орієнтуватися при збільшенні статистики. Якщо ви збільшили статистику в 100 разів, то слід очікувати що і час розрахунку збільшиться в 100 разів.

= Fmc_Uniform. Повертає випадкове число з рівномірним розподілом від Left до Right. Очевидно, що датчик fmc_Uniform легко виходить з датчика fmc_Rand, все, що потрібно зробити – вказати значення Left до Right. Відзначимо, що насправді байдуже в якому порядку показати кінці інтервалу Left і Right – датчик буде працювати коректно.

= Fmc_Normal. Повертає нормально розподілену випадкову величину із середнім значенням Mean і стандартним відхиленням STDev. Використовується частіше всіх інших разом взятих.

Параметри розподілу можна вводити числами або посиланнями на комірки. Однак при моделюванні попиту, наприклад, може виявитися, що частина гістограми розташована в негативній області осі, що відповідає негативному попиту. Це виходить при великих значеннях параметра StDev (при StDev > ~ ¹/₃Mean). Наприклад при значеннях параметрів Mean = 10 і StDev = 5 (= fmc_Normal (10, 5)) вийде наступна гістограма з негативним «хвостом»

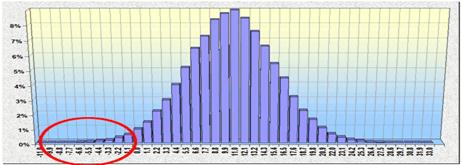
Щоб отримати коректні значення попиту потрібно використовувати функцію = ЕСЛИ (..) і вважати, що при негативних значеннях датчика попит був нульовий.

	A
	=fmc_Normal(10;5)
	=ЕСЛИ(A1<0;0;A1)

У цьому випадку вся негативна частина розподілу (гістограми) буде зібрана в одному стовпці – нульовому. Це відповідає реальному положенню подій – при високій варіативності попиту нульові продажі трапляються частіше, ніж невеликі. Швидкодія цього датчика приблизно в 1.5 рази менше, ніж у fmc_Rand.

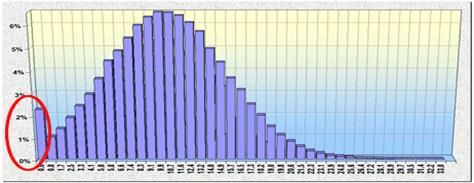
= Fmc_Discrete (Values; Probabilities). Повертає дискретну випадкову величину із заданим частотним розподілом: Values - Probabilities. У багатьох випадках неможливо (або немає сенсу) встановити конкретний вид функції розподілу випадкової величини. Найчастіше це пов’язано з малим числом можливих результатів. Однак якщо відомі ймовірності всіх можливих результатів, можна моделювати випадкову величину за таблицею. Наприклад, нехай можливі три результати випробувань: програш 10 тис., виграш 10 тис. і виграш 50 тис. грн. Оцінки ймовірності цих подій є (дивись табличку).

	A	B
	Values	Probabilities
	-10	35%
		60%
		5%

Викликаємо функцію fmc_Diskrete і показуємо, що виграші Values містяться в комірках A2: A4, а ймовірності Probabilities в осередках B2: B4.

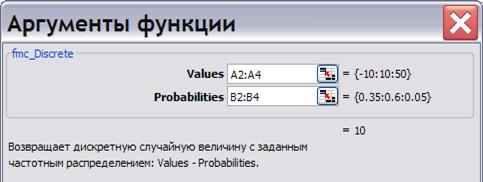
Гістограма, отримана в результаті моделювання Монте-Карло виглядає наступним чином:

= Fmc_ExhaustTime ( Inventory; Mean; StDev ). Повертає випадкову величину часу витрачання запасу Inventory при середньому споживанні Mean і стандартному відхиленні попиту StDev. Цей датчик розроблений для моделювання систем управління запасами і може бути використаний для оцінки ризику дефіциту при заданому рівні безпечного резерву (safetystock), для розрахунку втрат через дефіцит і для визначення оптимального ризику дефіциту. Передбачається, що попит клієнтів розподілений нормально (як це і буває в переважній більшості випадків). Датчик вимагає введення трьох чисел: запасу складу на поточний момент Inventory, середнього рівня попиту Mean і характеристики варіативності попиту (стандартного відхилення) StDev. Ці величини при введенні в інтерфейсі датчика можна вказати числами або послатися на комірки, що містять потрібні числа.

	A	B	З
	Inventory	Mean	StDev

Викликаємо функцію fmc_ExhaustTime і показуємо, що запас Inventory потрібно взяти з комірки A9, середній попит Mean з комірки B9, а стандартне відхилення попиту StDev з комірки C9.

Очевидно, що при нормально розподіленому попиті і час вичерпання запасу матиме нормальний розподіл.

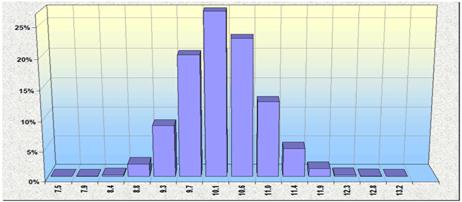
Не можна сказати, що без датчика fmc_ExhaustTime неможливо обійтися. Дійсно, подібний розрахунок можна побудувати прямо на аркуші Excel, використавши датчик fmc_Normal для моделювання попиту. На жаль, при цьому виходять дуже громіздкі і незручні схеми розрахунку. Датчик fmc_ExhaustTime дозволяє приховати непотрібні подробиці розрахунку і зосередитися на суті справи.

Швидкість розрахунку з датчиком fmc_ExhaustTime приблизно в 10 разів менше, ніж з fmc_Rand, що не дивно, враховуючи багаторазовий виклик датчика fmc_Normal для моделювання попиту.

Коли ми говоримо про нормально розподіленому попиті, необхідно пам’ятати, що попит не буває негативним (не будемо враховувати повернення товару), але датчик нормально розподіленої випадкової величини fmc_Normal, тим не менш, може видати негативне число. Імовірність такої події особливо велика, якщо стандартне відхилення StDev більше ¹ / ₃ від середнього попиту Mean.

При розрахунках усередині датчика fmc_ExhaustTime в разі отримання від’ємного значення попиту на черговому відрізку часу, попит, природно, прирівнюють до нуля. Це означає, що середнє значення попиту, розраховане за результатами моделювання, не буде одно Mean (буде більше) при великих StDev. Я планую додати на сайт і в книгу приклад коректних розрахунків в такій ситуації, а поки просто звертаю увагу користувачів на необхідності врахування такого розходження.

= Fmc_Exponential. Повертає експоненціально розподілену випадкову величину із середнім значенням Mean.

= Fmc_Triangula. Повертає випадкову величину з трикутним розподілом з нижньою межею Pessimistic, очікуваним значенням Mostprobable і верхньою межею Optimistic. Як говорили класики – не буває.

= Fmc_CorrNorm ( CorrMatrix; Means; STDevs ). Повертає масив нормально розподілених випадкових величин із середнім значенням Means, стандартними відхиленнями STDevs і кореляційної матрицею CorrMatrix.

Переваги методу Монте-Карло:

1. Допомагає у визначенні інвестиційних можливостей.

2. Надає можливості збільшити чисельність прийнятих рішень за граничним проектом.

3. Допомагає формувати інформаційну базу для полегшення ефективного розподілу ризиків і управління ними серед сторін, залучених в проект.

4. Направляє процес збору інформації проекту в такі галузі, які вимагають подальшого відзначення та розгляду.

5. З метою урахування інтересів і потреб інвестора, перегруповує проекти.

6. Згладжує і упереджує відносини між дослідником і зацікавленою особою, відповідальною за прийняття рішення.

7. Потребує ретельного перегляду показників, виражених єдиною цифрою в ході детермінованої оцінки.

8. Знижує упередженість при оцінці проекту.

9. Впливає на ефективну робот експертів.

10. Формує рамки для оцінки прогнозів результатів проекту.

11. Сприяє вимірюванню явних проблем з ліквідністю і визначенню та погашенню заборгованості з погляду часу і вірогідності того, що вони можуть мати місце протягом терміну експлуатації проекту.

Застосування даного методу на практиці демонструє широкі можливості його використання в інвестиційному проектуванні, особливо в умовах невизначеності і підвищеного ризику. Даний метод зручний для практичного застосування тим, що вдало корелює з іншими економіко-статистичними методами, а також з теорією ігор. До того ж він надає більш оптимістичні оцінки порівняно з іншими методами.

Оскільки, фінансові ризики пов’язані з категорією невизначеності, що обумовлює стохастичну форму взаємозалежності, то доцільно буде зупинитися на сучасних концепціях моделювання взаємозв’язку фінансових ризиків.

Загальна форма стохастичної взаємозалежності моделюється сучасним апаратом теорії ймовірностей у вигляді спільної функції розподілу характеристик фінансових ризиків. Але, оперування з функціями розподілу не є ефективним як з точки зору практичного ризик-менеджменту, так і у межах фінансової теорії. Тому відображення взаємозв’язку окремих фінансових ризиків здійснюється за допомогою певних числових мір взаємозв’язку.

До середини 1990-х років домінуючою мірою взаємозв’язку фінансових ризиків виступала кореляція. Але розвиток фінансових ринків, виникнення складних, нелінійних фінансових інструментів, об’єктивна складність характеристик портфеля фінансових інститутів наприкінці 1990-х років явно окреслили обмеженість кореляції як міри взаємозв’язку фінансових ризиків. Останнє вимагало нових концептуальних підходів до відбиття взаємозв’язків у складному, нелінійному, далекому від умов нормальності розподілів, фінансовому середовищі. В результаті у процедури моделювання фінансових ризиків в останні роки було імплементовано декілька нових концепцій копули та комонотоності.

Можна виділити наступні основні сучасні концепції моделювання взаємозв’язку фінансових ризиків:

– концепція кореляції;

– концепція копули;

– концепція ко-монотонності;

– концепція конкордаці.

Розглянемо переваги та не недоліки даних концепцій біьш детально.

Найбільш розповсюдженою концепцією математичного представлення взаємозв’язку фінансових ризиків у сучасній фінансовій теорії та практиці ризик-орієнтованого менеджменту є концепція кореляції. Сучасна проблематика фінансового ризик-менеджменту вказує на недостатність концепції кореляції для адекватного відбиття ризику портфеля. Подібне пояснюється наступними аспектами:

– кореляція адекватно відбиває залежність лише в галузі фінансових ризиків, представлених нормальними розподілами.

– коефіцієнт кореляції відбиває визначається коректно лише для фінансових ризиків, представлених випадковими величинами із скінченим другим моментом, в інших випадках коефіцієнти кореляції не визначені.

– коефіцієнти кореляції не є інваріантними відносно нелінійних фінансових ризиків.

Саме тому в сучасних умовах концепцій моделювання взаємозв’язку, яка вирішує частину вищезазначених проблем, пов’язаних з використанням кореляції як міри взаємозв’язку, є концепція копули.

Концепція копули як міри взаємозв’язку була розвинута у теорії ймовірностей у 1950-ті роки, але потужна імплементація даної концепції в інструментарій моделювання фінансових ризиків розпочалася наприкінці 1990-х років. На сьогодні концепція ефективно використовується при моделюванні взаємозалежності кредитних, ринкових, страхових та інших ризиків.

Сутність концепції полягає в наступному. Нехай розглядається n фінансових ризиків, представлених випадковими величинами Хі … Хв, з (безумовними) функціями розподілу F1….Fn. Ризик портфеля фінансових ризиків моделюється на основі спільної функції розподілу окремих ризиків:

F(x_і,…x_n) = P (X₁ < x_i,…, X_n < x_n)

Ідея застосування копули полягає у розподіленні на дві частини – перша відповідає безумовним розподілам F₁…Fn, а друга – власне залежності між F_i….F_n.

Копула порядку n є функцією С (u_i….u_n), визначеною на [0;1] із значеннями в інтервалі [0;1], яка задовольняє трьом властивостям:

1) С (u_i,….,u_n) є зростаючою функцією по кожній компоненті u_i;

2) С (l,…l, u_i, 1…1) = u_n для всіх і, u_i €[0;1];

3) Для довільного «прямокутника» в n-вимірному просторі {a₁ < x₁ < b_i; a₂ < x₂ < b₂;…; a_n < x_n < b_n} виконується нерівність:

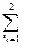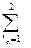… (-1)^{i1+…+ in} C (x_{1in, ….,} x_nin) > 0,

де, х_j1 = а_j та х_j2 = b_j для всіх j = 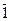, n

Властивості представлені в пунктах 1) – 3) є природними з огляду на те, що копула являє собою багатовимірну функцію розподілу. Зокрема, властивість 3 характеризує невід’ємність ймовірності кожного «прямокутника» в n-вимірному просторі.

Вельми важливою концепції копули є теорема Шкляра, яка з точки зору фінансового моделювання, обумовлює розділення окремих ризиків та ризиків портфеля (породжених залежністю між ними).

Теорема Шкляра. Якщо F – n-вимірна функція розподілу з безумовними неперервними розподілами F_1,…,F_n, то існує єдина копула С, така що:

F(x_i,…., x_n) = C (F₁(x₁),…, F_n (x_n)).

Вірним є і зворотне твердження: будь-яка функція з властивостями 1)–3) породжує n-вимірну функцію розподілу з безумовними неперервними розподілами F₁,…,F_n.

У випадку, коли функції розподілу не є неперервними, твердження теореми Шкляра залишається вірним, але копула вже може виявитися не єдиною.

Найпростішими прикладами копули є наступні:

С₀ (u_1,…,u_n) = u_{1 *} u_{2 *} … _* u_n,

яка відповідає випадку незалежних випадкових величин.

С₊ (u₁ ,…, u_n) = min (u₁, u₂, …, u_n),

яка характеризує позитивний ступінь залежності.

С_- (u₁, …, u_n) = max (u₁ + u₂ +…+ u + 1 – n, 0),

яка характеризує негативний ступінь залежності.

Наведені три копули відіграють при моделюванні залежності роль, аналогічну ролі коефіцієнтів кореляції «0», «1», «-1» для нормальних розподілів. В основі даного твердження лежить нерівність Фреша для копул, яка полягає в тому, що для будь-якої копули виконується нерівність:

С_- (u₁,…, u_n) < C (u₁,…, u_n) < C₊ (u₁,…, u_n).

Проаналізуємо перспективи застосування концепції копули в процедурах моделювання фінансових ризиків.

Концепція копули може більш адекватно відбивати структуру залежності між фінансовими ризиками, особливо у випадках моделювання неперервними випадковими величинами.

Концепція копули дає можливість конструювати структуру залежності між окремими ризиками підбором відповідної копули та «регулювати» ступінь залежності вибором параметру, включеного д копули.

Копула має таку зручну властивість (якої позбавлені коефіцієнти кореляції) як інваріантність відносно строго монотонних перетворень безумовних розподілів. Дана властивість дає можливість змінювати шкалу виміру, переходити від арифметичної до геометричної доходності без зміни копули.

Копула визначається безпосередньо через функції розподілу, що встановлює взаємозв’язок з квантильними мірами фінансових ризиків, зокрема Value-at-Risk.

Разом із тим, існує низка проблем, пов’язаних із застосуванням копули на практиці. Однією з таких проблем є з’ясування вигляду копули на основі емпіричних спостережень. Така задача може виявитися складною та вимагатиме спеціальних статистичних підходів. Подібні підходи повинні бути двоетапними: на першому етапі здійснюється оцінка безумовних розподілів окремих фінансових ризиків, а на другому етапі моделюється вигляд копули двох чи більше фінансових ризиків. На практиці останній крок виявляється найскладнішим.

Концепція ко-монотонності. При моделюванні фінансових ризиків часто зустрічається ситуація при якій випадкові величини, якими відбито фінансові ризики, є функціями від деякої іншої випадкової величини. Типовим прикладом подібної ситуації є наявність у портфелі акцій та опціонів Call і Put на дану акцію. В таких випадках може бути запроваджено спеціальний спосіб відображення залежності фінансових ризиків, який відбиватиме залежність більш адекватно, ніж кореляція чи копула.

Розглянемо сутність концепції спочатку на прикладах. Нехай інвестор має акцію А з ціновою динамікою в часі S_A(t), t > 0. Розглянемо опціони Call та Put європейського типу на акцію А з ціною виконання К та часом виконання Т>0. Фінансовий ризик інвестування в акцію А відбивається випадковою величиною S_A(T).

Доход за опціоном Call дорівнюватиме: С_А(Т) = (S_A(T) – K), = max (S_A(T); 0).

Доход за опціоном Put дорівнюватиме P_A(T) = (K – S_A(T)), = max (K – S_A(T); 0).

Як бачимо, доход за опціоном являє не спадну функцію від цін акції, а доход за опціоном Put – не зростаючу функцію.

Розглянемо три види портфелів:

– портфелі з акцій А та опціонів Call;

– портфелі з акцій А та опціонів Put;

– портфелі з опціонів Call та Put.

Вартість наведених портфелів моделюється двовимірними випадковими векторами: (S_A(T), C_A(T)), (S_A(T), P_A(T)), (C_A(T), P_A(T)) відповідно.

Портфель (S_A(T), C_A(T)) має наступну характерну властивість для двох довільних значень ціни s₁(T) та s₂(T), для виплати за опціоном буде виконуватися c₁(T) < c₂(T). Така властивість двох випадкових величин називатиметься ко-монотонностю.

Портфель (S_A(T), P_A(T)) має протилежну властивість: для довільних двох значень ціни s₁(T) та s₂(T), таких що s₁(T) < s₂(T), доходи за опціоном будуть протилежні p₁(T) > p₂(T). Подібна властивість двох випадкових величин називатиметься оберненою монотонності.

Портфель (C_A(T), P_A(T)) також має властивість оберненої монотонності – доход за опціоном Coll передбачає відсутність доходу за опціоном Put. Даний портфель має властивість генерувати доход в будь-якому випадку окрім рівності ціни S_A(T) = K.

Визначення ко-монотонності. Два ризики, представлені випадковими величинами X та Y, називаються ко-монотонними, якщо існує випадкова величина Z та неспадні функції f_x та f_y, що X = f_x(Z) та Y = f_y(Z).

Визначення оберненої монотонності. Два ризики, представлені випадковими величинами Xта Y, називаються обернено монотонними, якщо існує випадкова величина Z та неспадна функція f_x та не зростаюча функція f_y, що X = f_x(Z) та Y = f_y(Z).

Концепція конкордації. Концепція конкордаціїшироко застосовується в експертних дослідженнях, коли експерти ранжують об’єкти за декількома характеристиками. За кожною характеристикою є ранжований ряд значень, а для двох характеристик буде ряд пар (x_1, y₁), (x₂, y₂) …. (x_n, y_n). Далі пари порівнюють між собою та перевіряють виконання умови ко-монотонності та оберненої монотонності. Загальна кількість порівнянь дорівнюватиме С 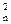_. Якщо кількість пар для яких виконується умова ко-монотонності, позначити с, а для яких виконується умова оберненої монотонності = d, то взаємозалежність буде представлена коефіцієнтом конкордації, який носить назву «тау Кендалла»:

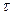= (с – d) / С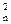

Якщо с>d, то коефіцієнт координації додатній, що аналогічно, в певному сенсі, додатній кореляції, а у випадку, коли кількість пар з оберненою монотонністю більше, тобто d>c, то коефіцієнт конкордації від’ємний, що свідчить про домінування обернено монотонних пар. Останній випадок ще називають «дискордацією».

Відмітимо, що концепції ко-монотонності та конкордації не передбачають використання ймовірності та базуються лише на порівнянні значень.

На закінчення сформулюємо властивості, які бажано, щоб задовольняли міри взаємозв’язку фінансових ризиків. Аналіз чотирьох представлених концепцій взаємозалежності дозволяє визначити такі властивості для числової міри взаємозв’язку (ğ):

1) Існування для всіх функцій розподілів (фінансових ризиків) з певного класу. Як ми бачили, коефіцієнт кореляції існує лише для ризиків, представлених випадковими величинами із скінченним другим моментом – в результаті, для значної кількості ризиків обчислити його неможливо. Копула існує для всіх розподілів, але лише для неперервних є єдиною.

2) Симетричність міри взаємозв’язку: ğ(X,Y) = ğ(Y,X). Дана властивість є цілком природною, і всі вищевикладені концепції – кореляції, копули, ко-монотонності та конкордації включають симетричні показники взаємозалежності.

3) Нормалізація І: –1 < ğ(X,Y) < 1.

4) Рівність 0 тоді і лише тоді, коли ризики X,Y незалежні.

5) Нормалізація ІІ. 0 < ğ(X,Y) < 1.

6) Умови 1,2,5 мають бути доповнені двома умовами моторності:

7) Монотонність І: ğ(X,Y)=1, тоді і лише тоді, коли X,Y ко-монотонні чи обернено монотонні.

8) Монотонність ІІ: Для довільної строго монотонної функції Т має виконуватися рівність ğ(Т(X),Y) = ğ(X,Y).

Міри взаємозв’язку, що задовольняють пункти 1), 2), 5), 6), 7) існують, принаймні для класу неперервних випадкових величин, але їх практичне застосування в моделюванні фінансових ризиків поки не розвинуте.

Дата добавления: 2014-11-29