Системы с нечеткими функциями выбора

ВЫБОРОЧНЫЕ ПЕРЕМЕННЫЕ ДЛЯ УПОРЯДОЧЕННЫХ МНОЖЕСТВ

Пусть имеется система полностью упорядоченных данных, которые необходимо перегруппировать для параллельной обра­ботки по нескольким каналам.

Рассмотрим задачу на конкретном примере, в котором сис­тема исходных данных (V₁,V₂,V₃) преобразуется с помощью мас­ки в систему (S₁;...S₆): S_i - номер ячейки наблюдений на поле маски:

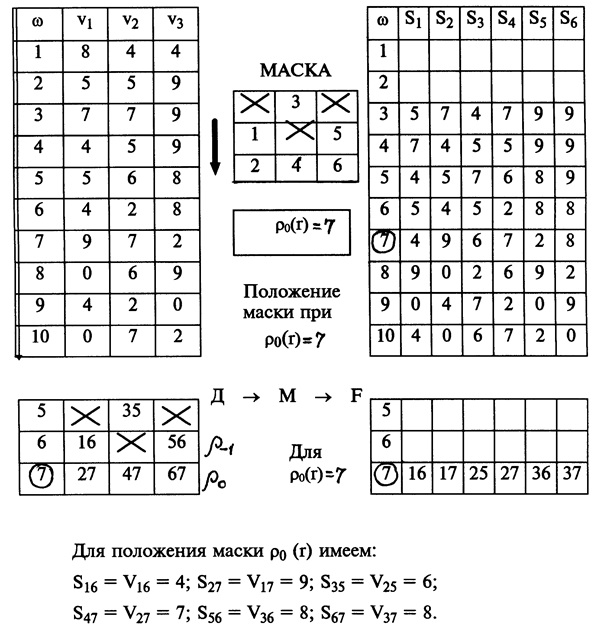
Маска для упорядоченной системы данных может быть представлена следующим образом:

	-r		+r
…	-1		+1	…

v1							W = T; t Î T t-1 – прошлое; t+1 – будущее; t0 – настоящее; r0 – справочник.
M:						V
vi
vn
	r0 = 0 R Ì W

Следовательно, уравнение для выборки данных имеет вид:

S_k,w Û S_k,t = V_i,t + r. (7.5)

Нечеткая функция выбора определяет состояние перемен­ной из универсума С на универсуме отрезка [0,1].

Структурированная система поведения из множества нечет­ких функций и правил, определяющих последовательности при­менения этих функций, является системой-моделью. Подобные классы моделей называются имитационными [21,22].

Мера нечеткости и ее свойства рассмотрены в п.4.2.

Нечетная функция поведения строится на основе экспери­мента непосредственно или после аппроксимации экспериментальных данных аналитической зависимостью, соответствующей одному из известных классов функций.

Рассмотрим теперь описание решения задачи в общем виде.

Пример 1. Поток событий в среднем равен 6 S/час. При эксперименте за единицу наблюдений принят пятиминутный ин­тервал времени. Результаты наблюдений за 1000 пятиминутных интервалов следующие:

k						å
n

Здесь к - число событий на интервале наблюдений,

n - количество интервалов с данным значением к Î{0, 1, 2, 3, 4}.

В этом случае нечеткая функция поведения определяет оценку вероятности попадания "К" - событий на интервал Dt = 5мин.; f_b:

k					å
pk	0,6	0,3	0,09	0,01

Для построения маски по известной функции поведения необходимо задать одно из разбиений универсума; например:

М: [0 ¸ 0.6) ® k = 0; [0.6 ¸ 0.9) ® k = 1;

[0.9 ¸ 0.99) ® k = 2; [0.99 ¸ 1.0) ® k =3.

Описание системы с нечетким поведением, т.е. F_b = (D, М, f_b), имеет следующее наполнение:

D - последовательность нормированных случайных чисел на выходе универсума [0,1); М - маской является универсум с задан­ным разбиением; f_b - нечеткая функция порождения, определяе­мая экспериментально.

Можно показать, что в приведенном конкретном примере f_b аппроксимируется рациональной системой, известной как закон распределения Пуассона:

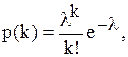
при l = 6 s/час = 0.5 s/5мин.

Схему системы нарождения F_b можно представить в виде механизма случайного выбора:

D

r_k

  М С В - К

K

Здесь r - случайное число, получаемое из D на интервале Dt с номером W; МСВ - К по сути маска М, но не обязательно для нормированных r. Так для двухразрядных случайных чисел МСВ - К в случае примера имеет вид, представленный на рис.7. 1.

k = 0 60 k = 1 89 k = 2 k = 3

00 59 90 98 99

Рис.7.1. Модель для имитации входного потока в систему массового обслуживания с нечеткими функциями поведения.

Правила поведения системы, процесс имитации поведения и обработки результатов эксперимента приведен в учебном посо­бии [21].

Упражнения

1. Функция порождения определена на пространстве со­стояний и переходов S = {S₀; S₁; … S₆} в виде матрицы условных вероятностей переходов | | p_ij | | и безусловных вероятностей со­стояний p_i = р(s_i).

Определите нечеткость следующих составляющих функций порождения:

а) для S₂, если р₂₁ = 4/18; р₂₂ = 9/18; р₂₃ = 3/18; р₂₄ = 2/18;

б) для {S_i}, если р₀ = 2/87; р₁ = 11/87; р₂ = 18/87; р₃ = 17/87;
р₄ = 16/87; р₅ = 18/78; р₆ = 5/87;

в) постройте соответствующие функции порождения.

2. В приложении П.4 приведена таблица случайных чисел.

Предложите правила выборки случайных чисел из таблицы с применением маски. Опишите правила выборки, используя сис­тему обозначений ячеек маски и правила сдвига.

3. Функции порождения для генераторов псевдослучайных чисел заданы рациональными системами и правилами поведения:

а. Метод срединных квадратов: взять 4- значное число (х₀), возвести в квадрат, получить 8- значное число (при необходи­мости добавить слева нули) (х₀²), выбрать из середины 4- значное число и т.д.:

x₀ ® x₀² ® x₁® x₁² ®...

б. Мультипликативный конгруэнтный метод:

x_i+1 = а*х_i(mod m);

x0*a	m
	B1 = x1 ® x1* a	m	;
		B2 = x2 ® …

х_i*а - х_i+1 = k*m;

х_i+1 - остаток от деления на m.

Требуется построить системы порождения с помощью масочных технологий, имитирующих процесс вычислений последо­вательностей псевдослучайных чисел.

Определите сходства и отличия случайных и псевдослучай­ных чисел. Приведите примеры использования указанных типов чисел в Вашей учебной деятельности.

ГЛАВА 8. ЭПИСТЕМОЛОГИЯ ЭМПИРИЧЕСКИХ СИСТЕМ

Дата добавления: 2014-12-07