Системы с нечеткими функциями выбора. Нечеткая функция выбора определяет состояние перемен­ной из универсума с на универсуме отрезка [0,1]

Нечеткая функция выбора определяет состояние перемен­ной из универсума С на универсуме отрезка [0,1].

Структурированная система поведения из множества нечет­ких функций и правил, определяющих последовательности при­менения этих функций, является системой-моделью. Подобные классы моделей называются имитационными [21,22].

Мера нечеткости и ее свойства рассмотрены в п.4.2.

Нечетная функция поведения строится на основе экспери­мента непосредственно или после аппроксимации экспериментальных данных аналитической зависимостью, соответствующей одному из известных классов функций.

Рассмотрим теперь описание решения задачи в общем виде.

Пример 1. Поток событий в среднем равен 6 S/час. При эксперименте за единицу наблюдений принят пятиминутный ин­тервал времени. Результаты наблюдений за 1000 пятиминутных интервалов следующие:

k						å
n

Здесь к - число событий на интервале наблюдений,

n - количество интервалов с данным значением к Î{0, 1, 2, 3, 4}.

В этом случае нечеткая функция поведения определяет оценку вероятности попадания "К" - событий на интервал Dt = 5мин.; f_b:

k					å
pk	0,6	0,3	0,09	0,01

Для построения маски по известной функции поведения необходимо задать одно из разбиений универсума; например:

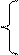М: [0 ¸ 0.6) ® k = 0; [0.6 ¸ 0.9) ® k = 1;

[0.9 ¸ 0.99) ® k = 2; [0.99 ¸ 1.0) ® k =3.

Описание системы с нечетким поведением, т.е. F_b = (D, М, f_b), имеет следующее наполнение:

D - последовательность нормированных случайных чисел на выходе универсума [0,1); М - маской является универсум с задан­ным разбиением; f_b - нечеткая функция порождения, определяе­мая экспериментально.

Можно показать, что в приведенном конкретном примере f_b аппроксимируется рациональной системой, известной как закон распределения Пуассона:

при l = 6 s/час = 0.5 s/5мин.

Схему системы нарождения F_b можно представить в виде механизма случайного выбора:

D

r_k

  М С В - К

K

Здесь r - случайное число, получаемое из D на интервале Dt с номером W; МСВ - К по сути маска М, но не обязательно для нормированных r. Так для двухразрядных случайных чисел МСВ - К в случае примера имеет вид, представленный на рис.7. 1.

k = 0 60 k = 1 89 k = 2 k = 3

00 59 90 98 99

Рис.7.1. Модель для имитации входного потока в систему массового обслуживания с нечеткими функциями поведения.

Правила поведения системы, процесс имитации поведения и обработки результатов эксперимента приведен в учебном посо­бии [21].

Упражнения

1. Функция порождения определена на пространстве со­стояний и переходов S = {S₀; S₁; … S₆} в виде матрицы условных вероятностей переходов | | p_ij | | и безусловных вероятностей со­стояний p_i = р(s_i).

Определите нечеткость следующих составляющих функций порождения:

а) для S₂, если р₂₁ = 4/18; р₂₂ = 9/18; р₂₃ = 3/18; р₂₄ = 2/18;

б) для {S_i}, если р₀ = 2/87; р₁ = 11/87; р₂ = 18/87; р₃ = 17/87;
р₄ = 16/87; р₅ = 18/78; р₆ = 5/87;

в) постройте соответствующие функции порождения.

2. В приложении П.4 приведена таблица случайных чисел.

Предложите правила выборки случайных чисел из таблицы с применением маски. Опишите правила выборки, используя сис­тему обозначений ячеек маски и правила сдвига.

3. Функции порождения для генераторов псевдослучайных чисел заданы рациональными системами и правилами поведения:

а. Метод срединных квадратов: взять 4- значное число (х₀), возвести в квадрат, получить 8- значное число (при необходи­мости добавить слева нули) (х₀²), выбрать из середины 4- значное число и т.д.:

x₀ ® x₀² ® x₁® x₁² ®...

б. Мультипликативный конгруэнтный метод:

x_i+1 = а*х_i(mod m);

x0*a	m
	B1 = x1 ® x1* a	m	;
		B2 = x2 ® …

х_i*а - х_i+1 = k*m;

х_i+1 - остаток от деления на m.

Требуется построить системы порождения с помощью масочных технологий, имитирующих процесс вычислений последо­вательностей псевдослучайных чисел.

Определите сходства и отличия случайных и псевдослучай­ных чисел. Приведите примеры использования указанных типов чисел в Вашей учебной деятельности.

ГЛАВА 8. ЭПИСТЕМОЛОГИЯ ЭМПИРИЧЕСКИХ СИСТЕМ

8.1. ЭПИСТЕМОЛОГИЯ ОСНОВНЫХ УРОВНЕЙ
ЭМПИРИЧЕСКИХ СИСТЕМ

Имена предметов, свойств, отношений, система коорди­нат и шкал отсчета образуют базис (базу) для выделения объек­та наблюдений. Проблема базирования и идентификации объ­екта рассмотрена в главе 2.

Понятие базы и системы базирования используется на всех уровнях абстрагирования и конкретизации системного описания. Например, базовые множества алгебраической струк­туры, базис линейного пространства, базисный полюс многополюсника, база транспортного средства, базовые и свободные переменные и т.п.

Система имен образует групповую основу идентификации объекта, система топологических свойств среды наблюдений образует пространственную и временную основу идентифика­ции.

Наполнение понятия базы изменяется от одного эпистемологического уровня описания объекта (как системы) к друго­му.

Уровень "0" - это примитивная система данных, уровень описания переменных и параметров (баз). В качестве парамет­ров выступают: время, пространство, совокупность объектов одного типа (социальные группы, группы стран, продукция од­ного типа и т.п.).

Данные классифицируются на входные и выходные, чет­кие и нечеткие... Входные переменные часто определяются как факторы. Факторы характеризуют среду системы. Воздействие наблюдателя - тоже фактор. Постановка факторного экспери­мента - одна из задач исследователя, решаемая на уровне фор­мирования примитивных данных как систем наблюдений.

При планировании экспериментов базовые переменные называются факторами. Остальные переменные называются от­кликами.

С понятием фактор пересекаются по своим свойствам та­кие понятия как вход, экзогенная (входная) переменная, аргу­мент функции, режим работы, независимая переменная.

Фактор является частным случаем базиса, при котором число точек наблюдений устанавливается экспериментатором.

С понятием отклик пересекаются такие понятия как вы­ход, эндогенная (выходная) переменная, функция, зависимая переменная, переменная состояния.

Множество откликов характеризуется поверхностью от­клика.

Построение поверхности отклика в базисе изначально управляемых переменных (факторов) - одна из задач фактор­ного планирования и анализа. Число точек наблюдений в пла­нируемом эксперименте определяется степенной функцией ви­да:

N = а*b^c,

где а - число повторений при статистических испытани­ях, b - число уровней фактора, с - число факторов.

План двухуровневого факторного эксперимента определя­ется алгебраической структурой вида N₁ ´ N₂ ® N₃, где N₁ - число наблюдений; N₂ - число факторов; N₃ Î {-1,1}, (-1) - минимальное значение фактора; (+1) - максимальное значение.

Исходная система (I) - пример нулевого уровня описания объекта наблюдения.

УРОВЕНЬ 1 - Это упорядоченная система данных. Дан­ные, как информация об объекте, должны быть представлены в виде, пригодном для дальнейшей обработки (вручную или ма­шинными средствами).

На этом уровне исследователь получает так называемый "информационный объект" - идентифицируемый объект реаль­ного мира [64].

База становится общей частью элемента данных, опреде­ляющих имя и метапараметры объекта, общая часть образует схему базы данных (БД).

Элемент данных связан со схемой БД и включает в себя значения переменных.

При проектировании БД применяются также понятия "ключа" и "атрибута".

Часть базы (схемы), однозначно идентифицирующая зна­чения переменных, называется ключом. Остальная часть базы характеризуется как атрибут.

Система упорядоченных примитивных данных (D) - ос­нова для проектирования информационного объекта базы дан­ных [64].

Данные могут быть отражением как результатов исследо­ваний, полученных по каналам наблюдений и абстрагирования в ходе эксперимента, так и описанием желательных состояний проектируемой системы.

УРОВЕНЬ 2 - Уровень порождающих систем, которые строятся на основе системы данных.

Систему генерируемых систем и их комплексов (моделей) определяют непосредственные связи параметров и переменных: уравнения связи входных и выходных данных, внутренние и внешние закономерности и характеристики, при­сущие данной предметной области знаний.

В общем случае они описываются соответствиями, ото­бражениями и отношениями множеств данных D, которые оп­ределяются с помощью правил преобразования (прямых и об­ратных, со свойствами изоморфизма или гомоморфизма):

D ® {f} ® F.

Первые три эпистемологических уровня описания определяют основную цепочку в системологии:

I ® D ® F.

Из данных трех общих типов систем с помощью опера­ций структуризации и метаопераций в системологии вводятся понятия структурированных систем и метасистем [1]. Цель по­добной классификации: определить методологические типы систем для решения классов системных задач [1,с.440].

Упражнение

1. В линейном программировании применяются понятия: "свободная переменная", "базовая переменная".

Каким понятиям факторного анализа соответствуют ука­занные переменные?

2. В двухальтернативной задаче статистических решений поверхность отклика для потерь статистика, определяемая по принципу минимакса, имеет вид функции [20]:

	a1	a2	x	M[q(x;h)] = åqijxi hj; x1+x1 = h1+ h2 = 1; 0 £ x1£ 1; 0 £ h2 £ 1.
v1	q11	q12	x1
v2	q21	q22	x2
h	h1	h2

Построение поверхности отклика рассмотрите как фак­торный эксперимент двух факторов x₁ и h₁ с планом для 2-х факторов и 4-х наблюдений. Определите математические свойства поверхности отклика, позволяющие построить поверхность отклика по данным факторного эксперимента, при плане:

x1	-1	-1
h1	-1		-1

3. Постройте поверхность отклика, задавшись значения­ми q_ij для случая, когда решение задачи лежит в области сме­шанных стратегий статистика.

Дата добавления: 2014-12-07