Тема: Кінематика. Рух тіла по колу

МЕХАНІКА

Рівномірний рух тіла по колу – найпростіший вид криволінійного руху. Будь-який складний рух тіла на достатньо малій ділянці його траєкторії можна наближено розглядати як рівномірний рух по колу.

При рівномірному русі по колу значення швидкості лишається сталим, а напрямок вектора швидкості 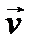змінюється в процесі руху. Визначимо прискорення тіла, що рухається рівномірно по колу радіусом R.

За інтервал часу Δt тіло проходить шлях ΔS=vΔt.

α

α

Δv

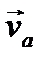
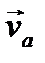
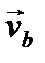
R

O

A

B

C

D

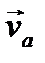Цей шлях ΔS дорівнює довжині дуги АВ. Вектори швидкостей і 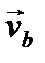в точках А і В напрямлені по дотичним до кола в цих точках, кут α між векторами 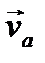і 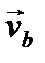дорівнює куту між радіусами ОА і ОВ.

Для знаходження вектора прискорення 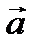необхідно знайти різницю векторів швидкості й визначити відношення зміни швидкості до малого проміжку часу Δt, за який відбулася ця зміна: .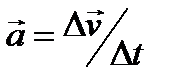

З подібності трикутників ОАВ та BCD виходить, що .

Якщо інтервал часу Δt малий, то малий кут α. При малих значеннях кута α довжина хорди АВ приблизно дорівнює довжині дуги АВ, тобто |AB|≈vΔt. Так як |ОА|=R, |AB|=vΔtі |CD|= Δv, то

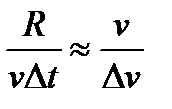
Звідси: .

Оскільки 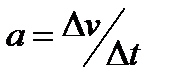, то .

Чим менший кут α, тим ближчий напрямок вектора 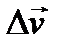до напрямку на центр кола.

Отже, під час рівномірного руху по колу модуль прискорення має стале значення, а напрямок вектора прискорення змінюється з часом. Таке прискорення називається доцентровим.

Якщо тіло рухається по колу нерівномірно, то поряд з доцентровим прискоренням (нормальним)

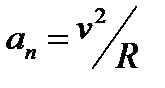
з’являється також дотична (тангенційна) складова прискорення

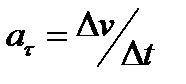, при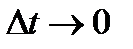

Напрямок вектора повного прискорення визначається

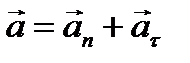
в кожній точці колової траєкторії величинами нормального і тангенційного прискорень.

Дата добавления: 2014-12-07