Закони Кеплера

Рух планет Сонячної системи не є безладним та невпорядкованим. Вони обертаються навколо Сонця згідно із законами, які на початку XVII століття відкрив видатний німецький учений И. Кеплера (1571–1630).

Еліпсом називається плоска замкнена крива, що складається з точок, сума відстаней від яких до двох даних точок F₁, тa F₂ є величиною. Точки F₁, тa F₂ називаються фокусами еліпса. Середина відрізка F₁F₂ точка О – центр еліпса. Відрізок АР=2а – називається великою віссю, а відрізки АО та ОР – великими півосями еліпса (АО=ОР=а) (мал.10).

Якщо М і N – довільні точки еліпса, то за означенням:

MF₁ + MF₂ = NF₁ + NF₂ = AF₁ + AF₂ = 2a.

Відношення = е називається ексцентриситетом еліпса і характеризує його витягнутість. Що більше витягнутий еліпс, то більший його ексцентриситет, проте у будь–якому випадку 0 < е < 1. Якщо е = 0, то еліпс перетворюється на коло.

Відрізок, що з'єднує довільну точку еліпса з одним з його фокусів, називається радіус–вектором цієї точки.

Перший закон Кеплера. Орбіти планет є еліпсами зі спільним фокусом, у якому міститься Сонце.

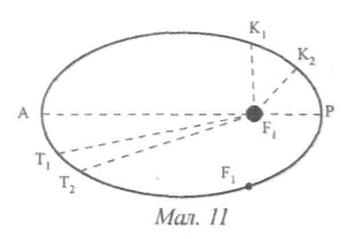
Рухаючись навколо Сонця, планета М періодично віддаляється та наближається до нього. Афелій – найдальша від Сонця точка траєкторії планети (т. А), перигелій – найближча точка (т. Р) (мал. 11).

Середня відстань від Сонця – це середнє арифметичне її афелійної та перигелійної відстаней, вона дорівнює великій півосі орбіти планети: а = 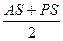. Лінія АР називається лінією апсид. Велика піввісь земної орбіти – одна астрономічна одиниця (1а.о.) – прийнята за одиницю довжини в астрономії.

Другий закон Кеплера. Радіус–вектор планети за однакові проміжки часу описує рівні площі (або секторна швидкість планети – величина стала).

Це означає: якщо за однакові проміжки часу планета проходить дуги K₁K₂ та Т₁Т₂, то площі секторів K₁K₂S та T₁T₂S рівні. За другим законом Кеплера, лінійна швидкість планети неоднакова у різних точках орбіти. Швидкість планети відносно Сонця поблизу перигелію найбільша, а поблизу афелію – найменша.

Третій закон Кеплера. Квадрати зоряних (сидеричних) періодів обертання планет належать як куби великих півосей орбіт.

.

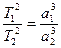Записавши третій закон Кеплера для Землі та іншої планети, маємо:

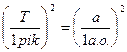,або

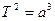
де Т – в роках, а – в а.о. Відкриття третього закону Кеплера дозволило обчислити відстані від Сонця до планет, періоди обертання яких же були відомі.

Запитання для самоконтролю

1. Що таке зоряний час, зоряна доба?

2. Коли сонячний і зоряний годинники показують однаковий час?

3. За яким принципом виконано поділ земної кулі на годинні пояси?

4. Які типи календарів ви знаєте?

5. Що таке нижні й верхні планети?

6. Зобразіть графічно перший закон Кеплера.

7. Зобразіть графічно другий закон Кеплера.

8. Запишіть математичний вираз третього закону Кеплера.

РОЗДІЛ ІІ. Наша планетна система. Сонце – найближча зоря.

ЛЕКЦІЯ №6

Тема.

Загальна характеристика планет сонячної системи. Планета Земля. Місяць. Штучні супутники Землі. Планети земної групи: Меркурій, Венера, Марс та їх супутники.

План лекції.

1. Загальна характеристика планет

2. Характеристика Землі

3. Місяць – супутник Землі.

4. Подібність та несхожість планет земної групи.

5. Меркурій

6. Венера

7. Марс

Література. Л4 (ст.49–55) Л5 (ст.75–86)

Дата добавления: 2014-12-07