Пример1

ВВЕДЕНИЕ В КИНЕМАТИКУ. ВЕКТОРНЫЙ СПОСОБ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ.

Кинематикой называется раздел механики в котором изучаются геометрические свойства движения тел без учета их инертности (масса) и действующих на них сил.

Кинематически задать движение или закон движения тела (точки), значит задать положения этого тела (точки) относительно данной системы отсчета в любой момент времени.

Основная задача кинематики состоит в том, чтобы зная закон движения данного тела (или точки), определить все кинематические величины, характеризующие как движение тела в целом, так и движение каждой из его точек в отдельности (траектории, скорости, ускорения).

Простейшим телом является материальная точка – тело малых размеров по сравнению с пространственными параметрами его движения.

1.Векторный способ задания движения

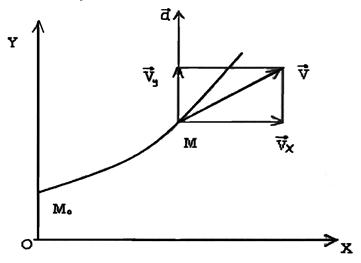
Радиус–вектор 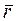(рис.1.1.), определяющий положение движущейся в пространстве точки М, меняет модуль и направление в зависимости от времени, т.е. является векторной функцией скалярного аргумента t. Уравнением движения точки называется зависимость радиуса - вектора от времени: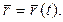

Годографом называется геометрическое место точек концов переменного радиус-вектора, отложенного из одной и той же точки.

Траекторией точки при векторном способе задания является годограф радиуса - вектора этой точки.

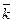
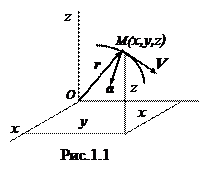Скоростью точкиназывается вектор, равный векторной производной от радиуса -вектора по времени.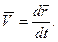

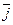
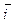Ускорением точки называется вектор, равный векторной производной от вектора скорости по времени.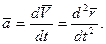

2.1 Координатный способ задания движения точки

Положение точки в пространстве относительно выбранной системы координат определяется координатами x, y, z.

Уравнения движения точки представляют собой зависимость координат движущейся точки от времени:

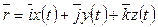
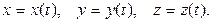
Определим скорость точки:

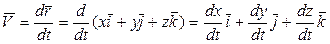
или

.

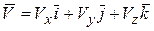Сравнивая эти два выражения, получим проекции скорости на оси координат:

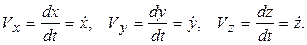
Модуль вектора скорости

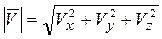
Направление вектора скорости определяется направляющими косинусами углов, которые вектор скорости образует с координатными осями (с положительным направлением осей):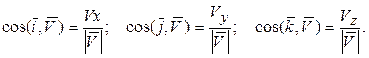

Проекции вектора ускорения на оси координат

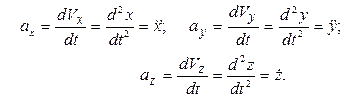
Модуль ускорения

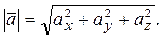
Направляющие косинусы вектора ускорения

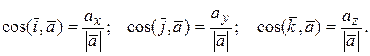
Движение точки М задается уравнениями:

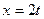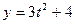см; см; .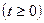

Определить кинематические элементы движения: траекторию, скорость и ускорение точки М. Указать момент времени, когда вектор скорости точки М образует с горизонтальной осью x-ов угол в 60⁰.

Построить годограф скоростей и ускорений.

Решение. Исключая из уравнений движения параметр t, найдем уравнение траектории: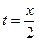

и

.

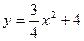Это есть уравнение параболы, симметричной относительно оси y-ов. Так как по условию 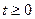, то 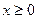и, следовательно, траекторией будет служить правая ветвь параболы. В начальный момент точка (t=0) находилась в вершине параболы (x=0, y=4).

Дифференцируя уравнения движения, найдем проекции скорости ускорения на координатные оси:

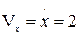см/сек; 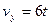см/сек.

Величина скорости равна:

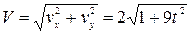см/сек.

Далее находим проекции ускорения на координатные ос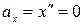и:

и 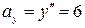см/сек².

Следовательно, ускорение в каждой точке траектории направлено по вертикали вверх и имеет постоянную величину, равную:

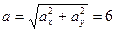см/сек².

Для того чтобы найти момент времени t=t₁, когда скорость точки М образует с осью х-ов угол в 60⁰, воспользуемся равенством:

.

Полагая здесь 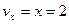, 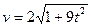и 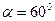, получим: ,

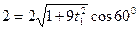Откуда следует: 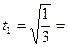0,57 сек.

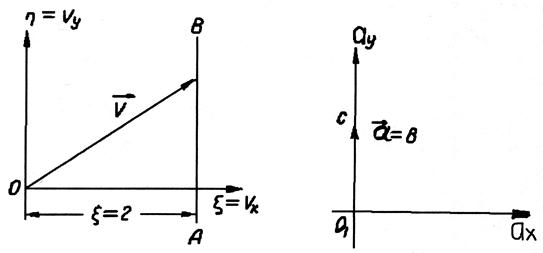
Годографом скорости будет служить прямая АВ, параллельная оси 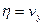с уравнением .

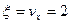Годографом ускорений будет служить точка С с координатами a_x=0 и a_y=6.

Дата добавления: 2014-12-07