Доказательство. Два вектора равны, если они равны по величине и одинаковы по направлению

Модуль векторного произведения:

.

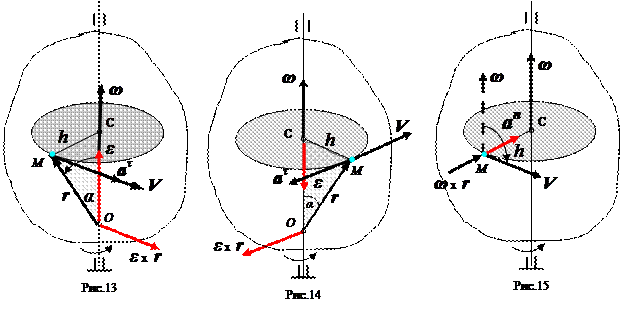
Векторное произведение 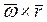направлено по перпендикуляру к плоскости треугольника ОМС, где лежат перемножаемые векторы, в сторону, откуда совмещение вектора угловой скорости с радиусом - вектором на меньший угол видно против часовой стрелки.

Вектор скорости 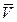лежит в плоскости, перпендикулярной оси вращения, и направлен по касательной к окружности в сторону вращения тела (перпендикулярен радиусу h) .

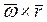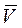Следовательно, направления векторов и совпадают, значит

.

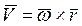Аналогично докажем, что вектор касательного ускорения выражается в виде векторного произведения:

Действительно: .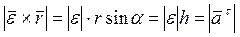

Вектор направлен (рис.13)по касательной к окружности, по которой движется точка и совпадает по направлению с вектором скорости точки, если векторы и направлены в одну сторону, что соответствует ускоренному вращению тела. Вектор направлен противоположно вектору скорости (рис.14), если вращение тела является замедленным, т.е. векторы и противоположны по направлению.

Вектор нормального ускорения точки также можно представить в виде векторного произведения:

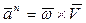
Действительно .

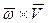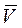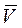Векторное произведение перпендикулярно векторам и и направлено по этому перпендикуляру так, чтобы с его конца совмещение вектора с вектором на меньший угол было видно против часовой стрелки. В соответствии с этим правилом вектор 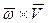направлен по радиусу вращения точки к центру окружности (рис.15), т.е. совпадает с вектором .

Дата добавления: 2014-12-07