
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Поступательное движение твердого тела. Естественный способ задания движения точки
|
|
|
|
Естественный способ задания движения точки
Этот способ применяется в том случае, когда траектория, по которой движется точка, известна. Выберем на траектории фиксированную точку О, (рис.1.2) и направление положительного отсчета дуги, тогда положение точки М в любой момент времени будет определяться значением дуговой координаты S=OM, отсчитываемой от точки О.
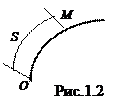 Законом движения точки называется зависимость дуговой координаты от времени:
Законом движения точки называется зависимость дуговой координаты от времени: 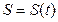 .
.
Введем единичный вектор 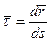 , направленный по касательной к траектории точки в сторону положительного отсчета расстояния s.
, направленный по касательной к траектории точки в сторону положительного отсчета расстояния s.
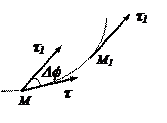 Вектор скорости точки равен
Вектор скорости точки равен
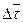
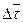


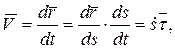
где 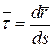 и
и 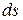 – дифференциал дуги траектории точки.
– дифференциал дуги траектории точки.
Тогда 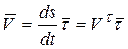 ,
, 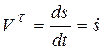 Проекция
Проекция 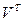 вектора скорости точки на касательную равна производной от дуговой координаты по времени.
вектора скорости точки на касательную равна производной от дуговой координаты по времени.
Если 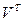 > 0, то скорость точки направлена в сторону положительного отсчета дуговой координаты, если
> 0, то скорость точки направлена в сторону положительного отсчета дуговой координаты, если 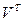 < 0, то скорость направлена в противоположную сторону.
< 0, то скорость направлена в противоположную сторону.
Выразим ускорение точки через характеристики естественного способа задания. Простейшей полоской кривой является окружность
Через 3 точки можно провести плоскость и
окружность с центром (СММ1,М2). Предельное
положение плоскости  , когда точки
, когда точки
 и
и  стремятся к точке
стремятся к точке  , называется
, называется
соприкасающейся плоскостью.
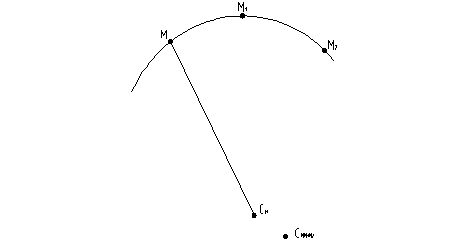
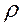
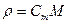 - радиус кривизны траектории в точке M
- радиус кривизны траектории в точке M
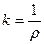 - кривизна
- кривизна
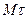 - касательная oрm
- касательная oрm 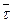 направлен по
направлен по
касательной в сторону возрастания
дуговой координаты
Mn - главная нормаль, opm 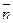
направленной по нормале,
лежащей в соприкасающейся
плоскости в сторону
вогнутости траектории
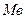 - бинормаль, opm
- бинормаль, opm 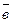 перпендикулярно
перпендикулярно
соприкасающийся
плоскости в ту сторону
откуда кратчайшее совмещение
оси 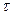 c n видно происходящим
c n видно происходящим
против хода часовой стрелки,
т.е. по правилу правого винта
Преобразуем выражение 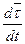 , учитывая, что
, учитывая, что 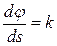 ,
, 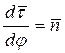 .
.
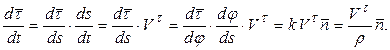
Тогда 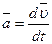 примет вид
примет вид
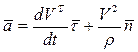 .
.
Вектор ускорения равен геометрической сумме векторов, один из которых 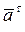 направлен по касательной, а другой
направлен по касательной, а другой 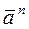 - по главной нормали.
- по главной нормали.
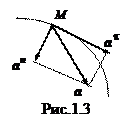 Ускорение т очки М лежит в соприкасающейся плоскости
Ускорение т очки М лежит в соприкасающейся плоскости
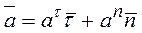
Касательное и нормальное ускорения определяются формулами:
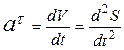 ;
; 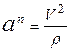
Величина 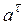 может быть положительной, отрицательной и равной нулю.
может быть положительной, отрицательной и равной нулю.
Модуль полного ускорения: 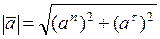
1. Если 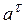 и
и 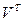 имеют одинаковые знаки (
имеют одинаковые знаки ( 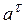 > 0,
> 0, 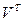 > 0 или
> 0 или 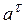 < 0,
< 0, 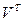 < 0), то движение точки будет ускоренным (рис.1.4, а ).
< 0), то движение точки будет ускоренным (рис.1.4, а ).
2. Eсли 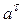 и
и 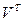 имеют разные знаки (
имеют разные знаки ( 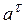 > 0,
> 0, 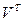 < 0 или
< 0 или 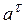 < 0,
< 0, 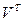 > 0), то движение будет замедленным (рис.1.4, б ).
> 0), то движение будет замедленным (рис.1.4, б ).
3. Если 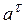 = 0, криволинейное движение точки будет равномерным (рис.1.4, с ).
= 0, криволинейное движение точки будет равномерным (рис.1.4, с ).
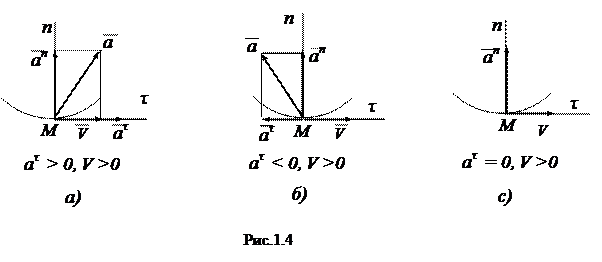 |
Касательное ускорение характеризует изменение скорости по величине. Величина нормального ускорения всегда положительна, это означает, что вектор
 направлен по главной нормали в сторону вогнутости кривой.
направлен по главной нормали в сторону вогнутости кривой.
Нормальное ускорение меняет скорость по направлению.
При равномерном движении точки по криволинейной траектории касательное ускорение равно нулю, так как модуль скорости движения является постоянным.
При прямолинейном движении нормальное ускорение равно нулю, так как в этом случае  .
.
Если движение точки является прямолинейным и равномерным, то и нормальное и касательное ускорения равны нулю.
При движении точки по окружности радиуса R нормальное ускорение равно 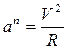 .
.
Лекция №6
Поступательным называется такое движение твердого тела, при котором любая прямая, жестко связанная с телом, перемещается параллельно самой себе.
Основное свойство: при поступательном движении все точки тела движутся одинаково, т.е. описывают одинаковые траектории и имеют геометрически равные скорости и ускорения.
Поступательное движение характеризуется движением любой его точки, поэтому для определения кинематических характеристик поступательного движения достаточно определить соответствующие характеристики одной из его точек.

Пример. Точка А кривошипа движется со скоростью VA = 0,8 м/с. ОА =0,4 м. Определить траекторию, скорость и ускорение точки М.
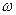
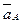
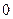
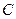
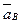
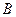
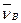
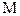
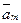
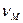
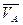
 Решение. Движение треугольной пластины ABM, соединенной шарнирно с кривошипами ОА и СВ, является поступательным, поэтому его можно характеризовать движением точки А. Точка описывает окружность радиуса ОА, скорость точки направлена по касательной к этой окружности, т.е. перпендикулярно ОА.
Решение. Движение треугольной пластины ABM, соединенной шарнирно с кривошипами ОА и СВ, является поступательным, поэтому его можно характеризовать движением точки А. Точка описывает окружность радиуса ОА, скорость точки направлена по касательной к этой окружности, т.е. перпендикулярно ОА.
Скорости всех точек пластины одинаковы и равны скорости точки А.
V М = VD = V A.
Точка А движется с постоянной скоростью, поэтому она имеет нормальное ускорение, направленное по кривошипу к точке О.
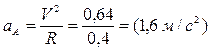
Ускорения всех точек пластины одинаковы и равны ускорению точки А:
а М = аВ = a A.
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 546; Нарушение авторских прав?; Мы поможем в написании вашей работы!