Краткая теория работы. Оборудование:торсионные весы, пипетка, сосуд с водой, маленькие легкие сосуды для взвешивания капель – бюксы (от немецкого Büchse – банка)

ОПРЕДЕЛЕНИЕ МАССЫ КАПЛИ ВОДЫ

Лабораторная работа № 2

Оборудование: торсионные весы, пипетка, сосуд с водой, маленькие легкие сосуды для взвешивания капель – бюксы (от немецкого Büchse – банка).

Цель работы: освоение методов статистической обработки результатов измерений (построение и анализ гистограммы, сравнение ее с кривой Гаусса); определение случайных погрешностей измерений.

Масса капли воды в каждом опыте вследствие влияния многочисленных факторов, большинство из которых невозможно заранее учесть, является случайной величиной. Поэтому заключение о массе капли может быть сделано лишь на основании статистической обработки результатов большого числа измерений. Причем, чем грубее используемый прибор, тем большее число измерений следует выполнить.

Если получаемые в результате измерений значения масс капель отложить на числовой оси, они образуют некий интервал, ограниченный минимальным и максимальным результатами. При этом не исключена вероятность того, что следующее измерение выйдет за пределы этого интервала. Поэтому при обработке результатов измерений задается вероятность попадания измеряемой величины в указанный интервал a, выражаемая либо в процентах, либо в частях (при выполнении лабораторных работ вероятность a обычно принимается равной 0,95). Интервал, соответствующий выбранной вероятности, называется доверительным интервалом. Ширина доверительного интервала равна двойной относительной погрешности D m, которая подсчитывается по формуле Питерса с учетом соответствующего коэффициента Стьюдента t _an(см. Элементы теории погрешностей):

,

где a – вероятность, n – число измерений, – среднестатистическое отклонение массы капли m _i от среднего ее значения :

.

Значения измеряемых величин распределяются по доверительному интервалу не равномерно, а подчиняясь статистическому закону распределения, описанному в свое время Гауссом. Для малых статистик, когда число измерений сравнительно невелико (порядка 10²), применяется метод гистограмм.

Гистограмма (от греческого histos - столб и... грамма), столбчатая диаграмма, один из видов графического изображения статистических распределений измеряемых величин по их численному значению. Она представляет собой совокупность смежных прямоугольников, одна из сторон которых, пропорциональная выбранному интервалу значений, лежит на общей прямой. Высота каждого прямоугольника соответствует числу попаданий измерений в соответствующий интервал.

В нашем случае по горизонтальной оси откладываются значения масс капель от минимального до максимального. Полученный отрезок разбивается на 5-6 равных интервалов (закрытых слева и открытых справа, поэтому последний интервал может иметь границу, превышающую максимальное значение на 1-2 единицы, определяемые ценой деления прибора). При этом ширина интервала включает только целое число единиц цены деления. По вертикальной оси откладывается относительное число капель N _i/ N ₀ (здесь N _i – число капель, приходящихся на данный интервал, N ₀ – общее число капель), массы которых соответствуют данному интервалу. На рис. 2.1 показан примерный вид гистограммы.

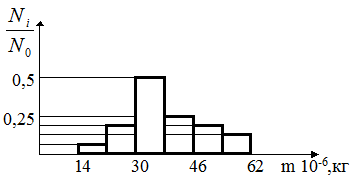
Рис. 2.1

Если центры верхних сторон прямоугольников, образующих гистограмму, соединить плавной кривой, то при правильном подборе количества интервалов для данного числа измерений полученная кривая приблизительно соответствует кривой Гаусса. Самой высшей точке этой кривой соответствует наиболее вероятное значение величины (его можно получить, опустив перпендикуляр на горизонтальную ось), оно обычно располагается левее среднего значения величины, хотя отклонение может быть и незначительным. Ширина кривой Гаусса на ее полувысоте обычно принимается за ширину доверительного интервала при вероятности 0,95, т.е. по кривой Гаусса можно определить абсолютную погрешность величины.

Дата добавления: 2014-12-07