Розв’язок. Для переходу від таблиці істинності булевої функції до ДКНФ можна скористатися наступним алгоритмом:

Для переходу від таблиці істинності булевої функції до ДКНФ можна скористатися наступним алгоритмом:

а) виділити в таблиці істинності булевої функції всі інтерпретації, на яких значення функції дорівнює нулю;

б) записати конституенти нуля, що відповідають відзначеним інтерпретаціям;

в) одержати ДКНФ функції за допомогою з’єднання операцією кон’юнкції записаних конституент нуля.

6 МІНІМІЗАЦІЯ БУЛЕВИХ ФУНКЦІЙ

6.1 Мета заняття

Ознайомлення c цілями мінімізації булевих функцій і способами визначення складності їх диз’юнктивних і кон’юнктивних нормальних форм. Вивчення методу мінімізуючих карт (діаграм Карно-Вейча).

6.2 Методичні вказівки з організації самостійної роботи студентів

Під час підготовки до практичного заняття необхідно повторити лекційний матеріал, розділи літератури [1-10] з таких питань: основні поняття і визначення, які використовуються при мінімізації булевих функцій; оцінка форми булевої функції за допомогою індексу (коефіцієнта) простоти; задача мінімізації булевих функцій в аналітичній і геометричній формі (задача про покриття); основні підходи для розв’язання задачі мінімізації булевих функцій у сучасній теорії й практиці алгебри логіки; операції диз’юнктивного і кон’юнктивного склеювання і поглинання; аналіз деяких аналітичних і геометричних методів одержання мінімальних ДНФ (КНФ) (метод Квайна-Мак-Класки, метод Порецького-Блейка, метод мінімізуючих карт (діаграми Карно-Вейча), метод багатомірних кубів та ін.); методика використання мінімізуючих карт (методика діаграм Карно і Вейча).

Підготовка і виконання практичного заняття проводиться у два етапи.

Перший етап пов’язаний з вивченням на практичних прикладах наступних основних понять і визначень: булевий базис; індекс (коефіцієнт) простоти; імпліканта; повна система імплікант; власна частина кон’юнкції; проста імпліканта; скорочена, тупикова ДНФ; мінімальна ДНФ (МДНФ); імпліцента, проста імпліцента, повна система імпліцент, скорочена, тупикова КНФ; мінімальна КНФ (МКНФ); неповне диз’юнктивне склеювання; диз’юнктивне поглинання; повне диз’юнктивне склеювання; неповне кон’юнктивне склеювання; кон’юнктивне поглинання; повне кон’юнктивне склеювання; мінімізуючі карти (діаграми Карно-Вейча).

При виконанні першого етапу практичного заняття студент повинен запропонувати і записати індивідуальний приклад для кожного з розглянутих вище понять і визначень. Другий етап виконання практичного заняття пов’язаний з розв’язанням практичних завдань, представлених у підрозділі 6.3, на основі запропонованих типових прикладів (див. підрозділ 6.4).

6.3 Контрольні запитання і завдання

6.3.1 Контрольні запитання

1. Що являє собою булевий базис? Чим обумовлений вибір базису при проектуванні логічних схем?

2. Що являє собою індекс (коефіцієнт) простоти? Наведіть приклади індексів простоти.

3. Які існують підходи для розв’язання задач мінімізації булевих функцій в аналітичному виді?

4. Запишіть формули операцій диз’юнктивного склеювання і поглинання.

5. Запишіть формули операцій кон’юнктивного склеювання і поглинання.

6. Дайте визначення термінам «імпліканта», «імпліцента», «проста імпліканта», проста «імпліцента».

7. Що являє собою скорочена ДНФ і скорочена КНФ?

8. Дайте визначення тупикової ДНФ. Скільки тупикових ДНФ може мати булева функція?

9. Яка із ДНФ (КНФ) називається мінімальною ДНФ (мінімальною КНФ)?

10. Що являють собою карти Карно (діаграми Вейча)?

11. Назвіть правило склеювання комірок і запису мінімальної ДНФ при використанні карт (діаграм) Карно.

12. Як здійснюється побудова карти Карно для функції п’яти змінних?

13. Опишіть особливості мінімізації булевих функцій на множині КНФ із використанням мінімізуючих карт.

14. Яким чином здійснюється мінімізація частково визначених функцій?

6.3.2 Контрольні завдання

Завдання 1. За допомогою співвідношень виду 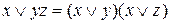перетворити ДНФ 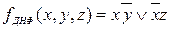до КНФ.

Завдання 2. Побудувати всі тупикові ДНФ наступних функцій:

а) ;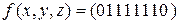

б) ;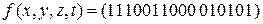

в) .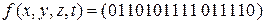

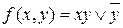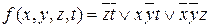Завдання 3. З’ясувати, чи є тупиковими або мінімальними наступні ДНФ: а) ; б) ; в) .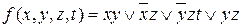

Завдання 4. Використовуючи карти Карно-Вейча, побудувати мінімальну ДНФ і мінімальну КНФ за таблицею істинності булевої функції 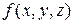(табл. 6.1).

Таблиця 6.1 - Таблиця істинності функції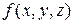

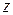
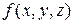
Дата добавления: 2014-12-07