Завдання 7

Методом невизначених коефіцієнтів побудувати поліном Жегалкіна для наступних функцій: а) ; б) ; в) , г) .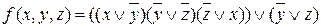

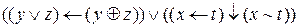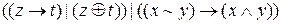Завдання 8. Провести дослідження на лінійність булевих функцій: а) ; б) ; в) .

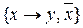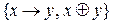Завдання 9. Довести повноту таких систем функцій шляхом зведення їх до відомих повних класів: а) ; б) ; в) .

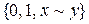Завдання 10. Перевірити на повноту такі класи функцій: а) ; б) ; в) .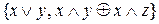

Завдання 11. За допомогою теореми Поста перевірити на повноту набори булевих функцій: а) , б) , в) , г) .

7.4 Приклади аудиторних і домашніх завдань

Завдання 1. Визначити, чи зберігає 0 і 1 функція .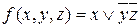

Розв’язок. Перевіримо значення даної булевої функції на нульовому й одиничному двійкових наборах: ; .

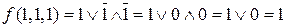Отже, дана функція зберігає 1 і не зберігає 0.

Завдання 2. Визначити відношення порядку для інтерпретацій функції і функції .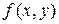

Розв’язок. Для функції однієї змінної маємо два набори змінних: (0) і (1). Відношення часткового порядку встановлюється таким чином: 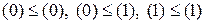. Тут усі пари порівнянні.

Для функції двох змінних 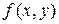маємо чотири набори змінних: 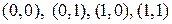, для яких відношення часткового порядку встановлюється так: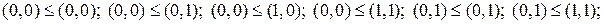 . Розглянуті набори є порівнянними, а набори 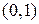і не є порівнянними.

Завдання 3. Провести дослідження на монотонність функції .

Розв’язок. Для функції запишемо всі набори значень змінних, для яких виконується відношення порядку, визначимо значення функції на даних наборах і порівняємо їх:

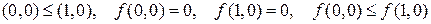
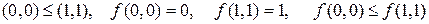
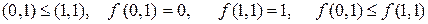
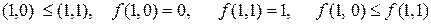
Функція є монотонною.

Завдання 4. Провести дослідження на монотонність функції .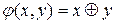

Розв’язок. Для функції 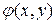запишемо всі набори значень змінних, для яких виконується відношення порядку, визначимо значення функції на даних наборах і порівняємо їх:

.

.

.

.

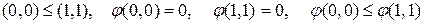Функція 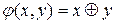не є монотонної, тому що при 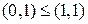не виконується умова .

Завдання 5. Побудувати поліном Жегалкіна для функції .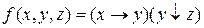

Розв’язок. Побудуємо поліном Жегалкіна, скориставшись наступним методом: 1) побудуємо еквівалентну формулу, використовуючи операцію кон’юнкції і заперечення; 2) замінимо 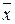на 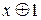і розкриємо дужки у формулі, користуючись законом дистрибутивності 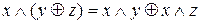. Дійсно виконуються такі рівності , , 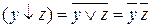звідки

,

Оскільки , то .

Завдання 6. Використовуючи метод невизначених коефіцієнтів побудувати поліном Жегалкіна для булевої функції трьох змінних, яка задається таким чином: .

Розв’язок. Поліном Жегалкіна для функції будемо шукати у вигляді:

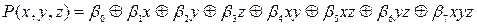, де .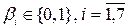

Коефіцієнти визначаються із рівності для довільного припустимого набору :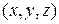

;

;

;

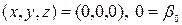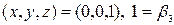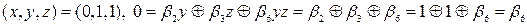, т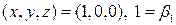ому ; ;

, тому ;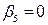

, отже ;

Отже, і .

Звідси поліном буде мати вигляд .

Завдання 7. Провести дослідження на лінійність функції .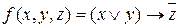

Розв’язок. Побудуємо поліном Жегалкіна функції 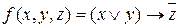, використовуючи такі тотожності: , .

.

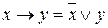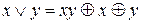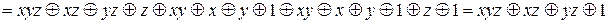Функція 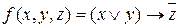не є лінійною, оскільки її поліном Жегалкіна містить кон’юнкції змінних.

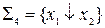Завдання 8. Системи (штрих Шеффера) і (стрілка Пірса) функціонально повні. Довести повноту систем і .

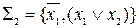Розв’язок. Проведемо такі перетворення: ,

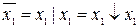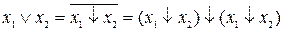; . Тому зводиться до , а 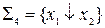зводиться до .

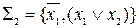Завдання 9. Перевірити на слабку функціональну повноту систему , що складається з однієї функції , яка задана таблицею істинності (табл. 7.1).

Таблиця 7.1 − Таблиця істинності функції

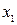
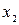
Розв’язок. Функція 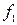немонотонна, тому що .

Побудуємо її поліном Жегалкіна:

.

Поліном Жегалкіна містить кон’юнкцію змінних, отже, функція 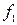нелінійна і система є функціонально повною в слабкому розумінні.

Завдання 10. Довести функціональну повноту системи .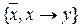

Розв’язок. Операцію заперечення можна представити поліномом Жегалкіна у вигляді 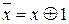, отже, функція заперечення лінійна. Функція заперечення є самодвоїстою, не зберігає 0, не зберігає 1 (це визначається з використанням таблиці істинності), немонотонна. Імплікація є нелінійною функцією, тому що її поліном Жегалкіна має вигляд 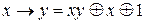, вона несамодвоїста, не зберігає 0, зберігає 1 (можна визначити з таблиці істинності функції), немонотонна. Отже, для кожного класу Поста в даній системі є хоча б одна функція, що цьому класу Поста не належить. За теоремою Поста така система булевих функцій є функціонально повною.

8 ЛОГІКА ТА ОБЧИСЛЕННЯ ВИСЛОВЛЕНЬ

8.1 Мета заняття

Ознайомлення c основними поняттями логіки та обчислення висловлень. Вивчення на практичних прикладах способів побудови та інтерпретації висловлень, методів перевірки правильності міркувань.

8.2 Методичні вказівки з організації самостійної роботи студентів

Під час підготовки до практичного заняття необхідно повторити лекційний матеріал, розділи літератури [1-10] з таких питань: елементарні висловлення (атоми); логічні зв’язки і формули логіки висловлень; логіка висловлень та її закони, ізоморфність алгебри логіки і логіки висловлень; пріоритет операцій алгебри висловлень; інтерпретація формул логіки висловлень, правильні міркування; логічна еквівалентність і логічний наслідок; обчислення висловлень (мова, система аксіом і правила висновку); повнота і несуперечність обчислення висловлень; вивідність в обчисленні висловлень (дедуктивний висновок, правила підстановки і відділення); різні аксіоматизації обчислення висловлень; деякі прийоми доведення в обчисленні висловлень.

Підготовка і виконання практичного заняття проводиться в два етапи.

Перший етап пов’язаний з вивченням на практичних прикладах таких основних понять і визначень: висловлення; атом; висловлювальна змінна; істиннісне значення; множина істиннісних значень; логічні зв’язки; формула логіки висловлень (молекула); заперечення висловлення; кон’юнкція, диз’юнкція, імплікація висловлень; засновок (умова, антецедент); логічний наслідок (висновок, консеквент); правильно побудована формула; логіка висловлень; інтерпретація висловлення; тотожно істинна формула; тотожно хибна формула; незагальнозначуща (несуперечлива) формула; правильне міркування; логічна еквівалентність; обчислення висловлень; мова обчислення висловлень; аксіоми обчислення висловлень; висновок в обчисленні висловлень; теорема дедукції; правила висновку; дедуктивний висновок; правило відділення; правило підстановки; несуперечливе логічне обчислення; незалежна система аксіом.

Під час виконання першого етапу практичного заняття студент, повинен запропонувати і записати індивідуальний приклад для кожного з розглянутих вище понять і визначень логіки і обчислення висловлень.

Другий етап виконання практичного заняття пов’язаний з розв’язанням практичних завдань, які надаються у підрозділі 8.3, на основі запропонованих типових прикладів (див. підрозділ 8.4).

8.3 Контрольні запитання і завдання

8.3.1 Контрольні запитання

1. Який вид речень моделює формальна логіка?

2. Дайте визначення поняття «висловлення».

3. Дайте визначення поняття «алгебра логіки висловлень».

4. Які висловлення називаються атомами?

5. Що в логіці висловлень називають логічними зв’язками?

6. Що в логіці висловлень називають молекулами?

7. Дайте характеристику алфавіту логіки висловлень.

8. Що мають на увазі в логіці висловлень під правильно побудованою формулою?

9. Дайте визначення логічного наслідку одного (декількох) висловлень.

10. Покажіть, що алгебра логіки і логіка висловлень є ізоморфними.

11. Яка формула називається тавтологією, тотожно хибною формулою, несуперечливою формулою?

12. Яке міркування називається правильним?

13. Перелічить найбільш важливі тавтології.

14. Які формули називаються рівносильними? Наведіть приклади рівносильних формул.

15. Що являє собою обчислення висловлень?

16. Поясніть поняття мови, аксіом і правил висновку обчислення висловлень.

17. Наведіть приклади аксіом обчислення висловлень.

18. Яким чином будується дедуктивний висновок?

19. Дайте стислу характеристику основних правил дедуктивного висновку.

20. Перелічить правила дедуктивних висновків логіки висловлень.

21. У чому полягає повнота і несуперечність обчислення висловлень?

22. Дайте визначення незалежної системи аксіом.

23. Сформулюйте теорему дедукції.

24. У чому полягає метод доведення від супротивного?

8.3.2 Контрольні завдання

Дата добавления: 2014-12-07