
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Розв’язок. Побудуємо карту Карно для заданої функції (рис
|
|
|
|
Побудуємо карту Карно для заданої функції (рис. 6.2).
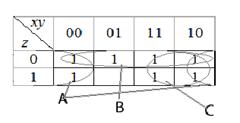
Рисунок 6.2 − Карта Карно для функції 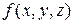
Мінімальна ДНФ буде представлена у вигляді  .
.
Завдання 5. Побудувати мінімальну диз’юнктивну нормальну форму функції 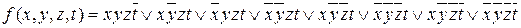 .
.
Розв’язок. Побудуємо відповідну карту Карно (рис. 6.3).

Рисунок 6.3 − Карта Карно для функції 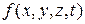
Запишемо мінімальну ДНФ, з’єднуючи диз’юнкцією прості імпліканти  :
: 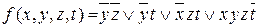 .
.
Завдання 6. Одержати мінімальну КНФ функції, яка задана ДКНФ:
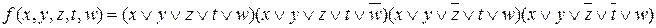
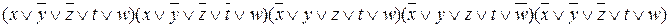
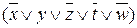 .
.
Розв’язок. Дана функція дорівнює нулю на наступних інтерпретаціях: (0,0,0,0,0), (0,0,0,0,1), (0,0,1,0,0,), (0,0,1,1,0), (0,1,1,0,0), (0,1,1,1,0), (1,0,0,0,0), (1,0,0,0,1), (1,1,1,0,0), (1,0,1,1,1). Карта Карно (діаграма Вейча) для даної функції буде мати вигляд, представлений на рис. 6.4.

Рисунок 6.4 − Карта Карно для функції 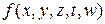
Запишемо мінімальну КНФ:
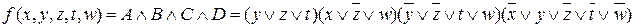 .
.
Завдання 7. Функція 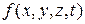 дорівнює одиниці на наборах (0,0,1,0), (0,1,1,0), (1,0,1,0), (1,0,0,0) і не визначена, якщо
дорівнює одиниці на наборах (0,0,1,0), (0,1,1,0), (1,0,1,0), (1,0,0,0) і не визначена, якщо  . Побудувати мінімальну ДНФ даної функції.
. Побудувати мінімальну ДНФ даної функції.
Розв’язок. Складемо карту Карно для заданої функції (рис. 6.5).

Рисунок 6.5 − Карта Карно для частково визначеної функції 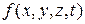
Мінімальна ДНФ буде мати такий вигляд 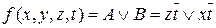 .
.
7 ФУНКЦІОНАЛЬНА ПОВНОТА НАБОРІВ БУЛЕВИХ ФУНКЦІЙ
7.1 Мета заняття
Ознайомлення c найважливішими замкненими класами булевих функцій (класами Поста), з поняттям повноти булевих функцій. Вивчення на практичних прикладах способів визначення типів булевих функцій і методу визначення функціональної повноти булевих функцій за допомогою теореми Поста.
7.2 Методичні вказівки з організації самостійної роботи студентів
Під час підготовки до практичного заняття необхідно повторити лекційний матеріал, розділи літератури [1-10] з таких питань: алгебра Жегалкіна, основні поняття; тотожності алгебри Жегалкіна; поліном Жегалкіна, методи його побудови і аналізу; визначення лінійності булевих функцій; типи булевих функцій; функції, що зберігають 0 і функції, що зберігають 1; монотонність булевих функцій, способи визначення монотонності булевих функцій; замкнення множини булевих функцій і замкнені класи; характеристика класів Поста; критерії повноти Поста; функціонально повна система функцій у слабкому розумінні; теорема Поста про функціональну повноту.
Підготовка і виконання практичного заняття проводиться за два етапи.
Перший етап пов’язаний з вивченням на практичних прикладах наступних основних понять і визначень: алгебра Жегалкіна; поліном Жегалкіна; довжина полінома Жегалкіна; ранг елементарної кон’юнкції; лінійна булева функція; функція, що зберігає 0; функція, що зберігає 1; монотонна булева функція; замкнення множини 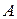 булевих функцій; замкнений клас; класи Поста; функціонально повна система функцій; функціонально повна система функцій у слабкому у слабкому розумінні; мінімально повний базис; нескоротна система булевих функцій.
булевих функцій; замкнений клас; класи Поста; функціонально повна система функцій; функціонально повна система функцій у слабкому у слабкому розумінні; мінімально повний базис; нескоротна система булевих функцій.
При виконанні першого етапу практичного заняття студент повинен запропонувати і записати індивідуальний приклад для кожного з розглянутих вище понять і визначень.
Другий етап виконання практичного заняття пов’язаний з розв’язанням практичних завдань, які представлені у підрозділі 7.3, на основі запропонованих типових прикладів (див. підрозділ 7.4).
7.3 Контрольні запитання і завдання
7.3.1 Контрольні запитання
1. Перелічить основні типи булевих функцій.
2. Дайте визначення булевих функцій, що зберігають 0 і 1.
3. Яка кількість всіх булевих функцій 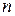 змінних зберігає константу 0 і константу 1?
змінних зберігає константу 0 і константу 1?
4. Яка функція називається монотонною булевою функцією?
5. Як, аналізуючи диз’юнктивну нормальну форму булевої функції, можна визначити, монотонна функція, чи ні?
6. Запишіть і поясніть структуру алгебри Жегалкіна.
7. Перелічить основні закони і тотожності алгебри Жегалкіна.
8. Дайте визначення поняттю поліному Жегалкіна.
9. Дайте визначення лінійності булевої функції.
10. Наведіть приклади лінійних і нелінійних функцій двох змінних.
11. Перелічить найважливіші замкнені класи булевих функцій.
12. Яка система булевих функцій називається функціонально повною?
13. Сформулюйте теорему про повноту двох систем булевих функцій.
14. Наведіть визначення функціональної повноти в слабкому розумінні.
15. Яка повна система булевих функцій є нескоротною.
16. Сформулюйте теорему Поста про повноту булевих функцій.
7.3.2 Контрольні завдання
Завдання 1. Визначити, чи зберігають 0 і 1 наступні булеві функції: а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 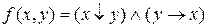 ; д)
; д) 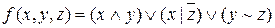 .
.
Завдання 2. Визначити кількість самодвоїстих функцій з числа всіх функцій 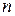 змінних
змінних  , де
, де 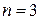 і
і  .
.
Завдання 3. Визначити відношення порядку для інтерпретацій функції 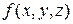 .
.
Завдання 4. Провести дослідження наступних функцій на монотонність: а) 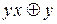 ; б)
; б) 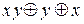 ; в)
; в) 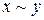 ; г)
; г) 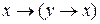 , д)
, д) 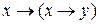 , е)
, е) 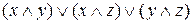 .
.
Завдання 5. Довести монотонність наступних функцій:
а) 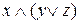 ; б)
; б) 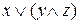 ; в)
; в) 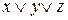 ; г)
; г) 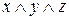 .
.
Завдання 6. Представити у вигляді полінома Жегалкіна наступні логічні функції: а) 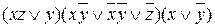 ; б)
; б) 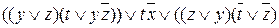 ; в)
; в) 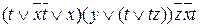 .
.
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 1394; Нарушение авторских прав?; Мы поможем в написании вашей работы!