Работа сил электрического поля по перемещению электрического заряда

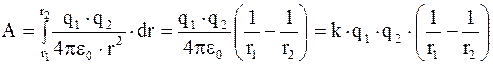, (3.21)

где k - коэффициент пропорциональности, зависящий от выбора системы единиц измерения физических величин. В системе СИ k = 1/4pe₀;

q₁ - заряд, создающий электрическое поле;

q₂ - заряд, перемещаемый в электрическом поле;

r₁, r₂ - начальное и конечное расстояния между зарядами.

Работа сил электрического поля по перемещению электрического заряда по любому замкнутому контуру L равна нулю:

. (3.22)

Потенциальная энергия электрического заряда, находящегося в электрическом поле другого заряда:

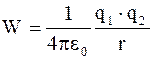. (3.23)

Изменение потенциальной энергии электрических зарядов равно работе сил электрического поля (консервативных сил), взятой с обратным знаком:

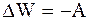. (3.24)

Потенциал электрического поля - скалярная энергетическая характеристика электрического поля; равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:

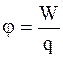. (3.25)

Потенциал электрического поля положительного точечного заряда:

, (3.26)

где q - величина заряда, создающего электрическое поле;

r - расстояние от центра заряда до рассматриваемой точки поля.

Потенциал электрического поля системы точечных зарядов равен алгебраической сумме потенциалов полей, создаваемых отдельно взятым зарядом системы:

, (3.27)

где q_i - величина i-го заряда;

r_i - расстояние от i-го заряда до рассматриваемой точки поля.

Разность потенциалов между двумя точками стационарного электрического поля - скалярная физическая величина, численно равная работе сил электрического поля по перемещению положительного единичного заряда из одной точки поля в другую:

. (3.28)

Связь между напряженностью и потенциалом электрического поля:

а) для произвольного направления l

, (3.29)

где 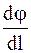- характеризует быстроту изменения потенциала в данном направлении;

знак "минус" - означает, что вектор напряженности электрического поля направлен в сторону уменьшения потенциала.

б) в векторной форме

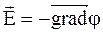, (3.30)

где grad j = 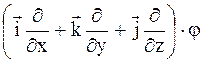- градиент потенциала.

Разность потенциалов между двумя точками электрического поля, которое создано бесконечно длинным равномерно заряженной нитью:

, (3.31)

где t - линейная плотность заряда;

r₁, r₂ - расстояния от рассматриваемых точек поля до оси стержня (цилиндра).

Разность потенциалов между двумя точками электрического поля, которое создано бесконечно протяженной, равномерно заряженной плоскостью:

, (3.32)

где s - поверхностная плотность зарядов;

d = (r₂ - r₁) - расстояние между рассматриваемыми точками поля.

Разность потенциалов между двумя точками поля, которое создано равномерно заряженной сферической поверхностью радиусом R:

, (3.33)

где s - поверхностная плотность заряда;

r₁>R; r₂>R - расстояние от центра сферы до рассматриваемых точек поля.

Потенциал поля вне сферической поверхности

, (3.34)

где r>R - расстояние от центра сферы до рассматриваемой точки поля.

Потенциал поля внутри сферической поверхности одинаков и имеет значение

. (3.35)

Разность потенциалов между двумя точками поля, которое создано равномерно заряженным по объёму шаром радиусом R:

, (3.36)

где r - объемная плотность заряда;

r₁>R; r₂>R - расстояние от центра шара до рассматриваемых точек поля.

Потенциал электрического поля на поверхности шара:

. (3.37)

Потенциал электрического поля внутри шара:

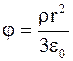, (3.38)

где r - расстояние от центра шара до рассматриваемой точки поля.

Эквипотенциальные поверхности - поверхности, все точки которых имеют один и тот же потенциал.

3.2. Проводники в электрическом поле

Проводники – вещества, хорошо проводящие электрический ток, т.е. обладающие высокой электропроводностью (малым удельным электрическим сопротивлением - r ~ 10^-6¸10^-8 Ом∙м).

Проводники первого рода - металлы и их сплавы, графит, некоторые окислы и сернистые соединения металлов.

Проводники второго рода - электролиты (растворы солей кислот и щелочей).

Плазма – сильно ионизированная почти нейтральная среда, в которой хаотическое движение частиц преобладает над их направленным движением под действием электрического поля.

Высокотемпературная (изотермическая) плазма возникает вследствие высокой температуры вещества.

Газоразрядная плазма – плазма, возникающая при газовом разряде.

Отличительные особенности проводников первого рода:

1) электрический ток в них представляет собой упорядоченное движение электронов проводимости, при этом никаких химических изменений в проводниках не происходит;

2) кристаллическое строение - последовательность правильно расположенных групп ионов, образующих пространственную кристаллическую решетку, в межузельном пространстве которой находятся электроны проводимости.

Условие перераспределения (движения) электрических зарядов в объеме проводника:

E = E ₀ + E ^' ¹ 0, (3.39)

где E - напряженность результирующего поля в объеме проводника;

E ₀ - напряженность внешнего электрического поля;

E ^' - напряженность "собственного" электрического поля.

Условие равновесия зарядов в проводнике:

E = E ₀ + E ^' = 0. (3.40)

Напряженность электрического поля вблизи поверхности заряженного проводника с поверхностной плотностью s:

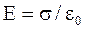. (3.41)

Электрическая емкость (электроемкость) уединенного проводника - физическая величина, численно равная количеству электричества, на которое необходимо изменить заряд проводника, чтобы его потенциал изменился на единицу. Зависит от формы поверхности, линейных размеров, расположения относительно других проводников, среды, окружающей проводник, и не зависит от его заряда и потенциала:

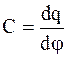, , . (3.42)

где Dq - изменение заряда проводника;

Dj - изменение потенциала проводника;

dq - элементарное изменение заряда проводника;

dφ - элементарное изменение потенциала проводника;

q - заряд проводника;

j - потенциал проводника.

Конденсаторы - устройство, состоящее из проводников, разделенных слоем диэлектрика (непроводника), способное накапливать значительные заряды.

Электроемкость конденсатора - физическая величина, численно равная отношению величины заряда одного знака к разности потенциалов между проводниками (обкладками, пластинами). Зависит от геометрических размеров, формы обкладок, среды, заполняющей пространство между обкладками, и не зависит от заряда и разности потенциалов между обкладками:

, (3.43)

где C - емкость конденсатора (взаимная емкость его обкладок);

q - заряд одной из обкладок (заряды обкладок равны по абсолютной величине, но противоположны по знаку);

U = j₁ - j₂ - напряжение на конденсаторе (разность потенциалов между обкладками).

Плоский конденсатор представляет собой устройство, состоящее из двух пластин (обкладок), расположенных на некотором расстоянии друг от друга. Пространство между обкладками заполнено слоем диэлектрика.

Емкость плоского конденсатора в системе СИ

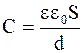, (3.44)

где e - относительная проницаемость среды, которая показывает, во сколько раз емкость конденсатора больше при наличии среды между его пластинами;

e₀ = 8,85∙10^-12 Ф/м - электрическая постоянная;

S - площадь одной из пластин;

d - расстояние между пластинами.

Цилиндрический конденсатор представляет собой устройство из двух цилиндрических обкладок, имеющих общую ось (коаксиальных), разделенных слоем диэлектрика цилиндрической формы.

Емкость цилиндрического конденсатора (коаксиального кабеля):

, (3.45)

где l - длина цилиндрических обкладок;

R₁ - радиус внутренней обкладки;

R₂ - радиус внешней обкладки.

Сферический конденсатор представляет собой устройство, состоящее из двух сферических поверхностей, которые имеют общий центр, различных радиусов, разделенных сферическим слоем диэлектрика.

Емкость сферического конденсатора:

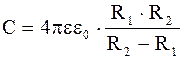, (3.46)

где R₁ - радиус внутренней сферы;

R₂ - радиус внешней сферы.

Соединения конденсаторов:

а) последовательное соединение - такое соединение, при котором каждая из обкладок какого-либо конденсатора соединяется только с одной обкладкой другого конденсатора (образуется цепочка конденсаторов).

Емкость системы при последовательном соединении конденсаторов меньше наименьшей из образующих систему емкостей:

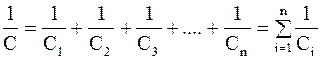. (3.47)

б) параллельное соединение конденсаторов - такое, при котором обкладки конденсаторов соединяются в группы, причем одна из обкладок каждого конденсатора соединяется в одну группу, а другая - в другую.

Емкость системы при параллельном соединении равна сумме емкостей конденсаторов, образующих систему, при этом она больше наибольшей из включенных:

C = C₁ + C₂ + C₃+....+ C_n = . (3.48)

3.3. Статическое электрическое поле в веществе

Статическое электрическое поле в веществе (диэлектрике) возникает в результате сложения двух полей: поля, создаваемого свободными зарядами, и поля связанных зарядов.

Свободные (сторонние) заряды – заряды, которые находятся в пределах диэлектрика, но не входят в состав его молекул (атомов), а также заряды, расположенные за пределами диэлектрика. Свободные заряды могут перемещаться в объеме диэлектрика и перераспределяться между соприкасающимися диэлектриками или внутри диэлектрика.

Связанные заряды (поляризационные) – заряды, "возникающие" в процессе поляризации диэлектрика. Они входят в состав молекул (атомов) диэлектрика.

“Центры зарядов” – воображаемые точки расположения положительного суммарного заряда и отрицательного суммарного заряда внутри диэлектрика (внутри атомов и молекул).

Положение “центров зарядов” внутри молекул определяется соответственно:

а) для положительных зарядов

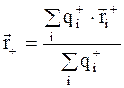; (3.49)

б) для отрицательных зарядов

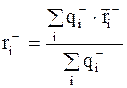, (3.50)

где r ₊, r _-, r _i⁺, r _i^- - соответствующие радиус - векторы, определяющие положение суммарных и отдельно взятых положительных и отрицательных зарядов;

q_i⁺, q_i^- - величина отдельно взятых зарядов.

Полярные молекулы - молекулы, у которых “центры зарядов” q₊ и q_- в отсутствие внешнего электрического поля не совпадают.

Собственный электрический момент полярных молекул:

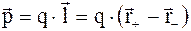, (3.51)

где l – радиус - вектор, соединяющий центры "тяжести" зарядов, направленный от отрицательного к положительному заряду.

Неполярные молекулы - молекулы, у которых в отсутствие внешнего электрического поля “центры зарядов” совпадают. При внесении неполярной молекулы во внешнее электрическое поле “центры зарядов” смещаются, она поляризуется, приобретает электрический дипольный момент, по величине пропорциональный напряженности внешнего электрического поля p ~ E.

Вращающий момент, действующий на диполь (молекулу) в однородном внешнем электрическом поле, стремится повернуть диполь так, чтобы его электрический дипольный момент был направлен по направлению внешнего электрического поля:

M = [ pE ]. (3.52)

Сила, действующая на диполь (молекулу) в неоднородном внешнем электрическом поле, либо втягивает диполь в область более сильного поля (a<p/2), либо выталкивает его из него (a>p/2):

, (3.53)

где a - угол между направлением электрического дипольного момента и вектором напряженности электрического поля.

Поляризация диэлектрика - процесс перераспределения связанных зарядов в диэлектриках во внешнем электрическом поле. Диэлектрик приобретает отличный от нуля электрический дипольный момент

. (3.54)

Виды поляризации диэлектриков:

1) деформационная наблюдается у диэлектриков, состоящих из неполярных молекул, заключающаяся в возникновении у молекул (атомов) индуцированного дипольного момента за счет деформации электронных орбит.

2) ориентационная, или дипольная, наблюдается у диэлектриков, состоящих из полярных молекул, заключающаяся в ориентации имеющихся дипольных моментов молекул (атомов) по направлению электрического поля.

3) ионная наблюдается у диэлектриков, имеющих ионную кристаллическую решетку, и заключается в смещении подрешетки положительных ионов вдоль поля, а отрицательных - против поля.

Вектор поляризации (поляризованность) - физическая величина, численно равная электрическому дипольному моменту единицы объема диэлектрика:

, (3.55)

где p _i – дипольный момент одной молекулы.

Однородная поляризация – такая поляризация, которая возникает у однородных диэлектриков, при этом вектор поляризации одинаков по всему объему.

Неоднородная поляризация – такая поляризация, для которой не выполняются условия однородной поляризации.

Связь вектора поляризации с вектором напряженности внешнего электрического поля – для большинства диэлектриков, кроме так называемых сегнетоэлектриков, вектор поляризации пропорционален напряженности внешнего электрического поля:

P = ce₀ E, (3.56)

где c - диэлектрическая восприимчивость вещества, не зависящая от напряженности внешнего электрического поля. Она характеризует способность вещества к поляризации.

Связь между вектором поляризации и поверхностной плотностью связанных зарядов: поверхностная плотность связанных зарядов численно равна нормальной составляющей вектора поляризации в данной точке поверхности диэлектрика:

s^’ = P_n, (3.57)

где s^’ – поверхностная плотность связанных зарядов;

P_n – нормальная составляющая вектора поляризации.

Связь между вектором напряженности внешнего электрического поля и поверхностной плотностью связанных зарядов:

s^’ = ce₀E_n, (3.58)

где E_n – нормальная составляющая вектора напряженности внешнего электрического поля.

Вектор электрической индукции (электрического смещения) – векторная физическая величина, которая связана с вектором поляризации и напряженностью электрического поля соотношением:

D = e₀ E + P. (3.59)

Связь между вектором напряженности и вектором индукции электрического поля:

D = (1 + c)e₀E = ee₀E, (3.60)

где e = (1 + c) – относительная проницаемость среды, величина которой зависит от структуры и химического состава вещества, а также от давления, температуры и других внешних факторов. Она показывает, во сколько раз электрическое поле ослабевает, если оно создано в какой-либо среде.

Напряженность электрического поля внутри диэлектрика всегда меньше, чем в вакууме в e раз:

, (3.61)

где E ₀ – напряженность электрического поля в вакууме;

E – напряженность электрического поля в диэлектрике.

Теорема Остроградского-Гаусса для потока вектора индукции электрического поля: поток вектора индукции электрического поля через любую замкнутую поверхность равен алгебраической сумме зарядов, находящихся внутри этой замкнутой поверхности:

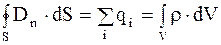. (3.62)

Граничные условия на поверхности раздела "диэлектрик-диэлектрик":

а) при переходе через границу раздела двух диэлектриков тангенциальная составляющая вектора E (E_t) и нормальная составляющая вектора D (D_n) не претерпевают скачка (изменяются непрерывно):

E_t1 = E_t2; D_n1 = D_n2; (3.63)

б) при переходе через границу раздела двух диэлектриков нормальная составляющая вектора E (E_n) и тангенциальная составляющая вектора D (D_t) претерпевают скачок:

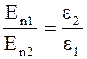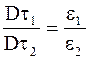; . (3.64)

Внутренняя энергия диэлектриков во внешнем электрическом поле

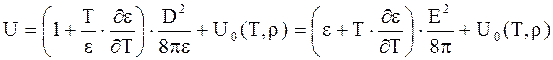, (3.65)

где функция U₀(T,r) - внутренняя энергия диэлектрика при отсутствие в нем электрического поля.

Свободная энергия системы, которая связана с электризацией тел:

. (3.66)

Свободная энергия системы, которая зависит от напряженности электрического поля:

. (3.67)

Основные уравнения термодинамики диэлектриков:

dU = T×dS + E×dD/4p; (3.68)

dF = - S×dT + E×dD/4p; (3.69)

dФ = - S×dT - D×dE/4p; (3.70)

dI = T×dS - D×dE/4p. (3.71)

Уравнение состояния:

D = f(E,T,r), (3.72)

где r - плотность вещества диэлектрика.

Электрострикция – деформация диэлектрика во внешнем электрическом поле. В изотропных средах, в том числе в газах и жидкостях, изменение плотности под действием электрического поля:

, (3.73)

где A = - коэффициент пропорциональности, зависящий от сжимаемости и плотности вещества;

b - сжимаемость;

r - плотность;

e - диэлектрическая проницаемость.

Сегнетоэлектрики – кристаллические диэлектрики, обладающие в определенном интервале температур спонтанной (самопроизвольной) поляризацией, которая существенно изменяется под влиянием внешних воздействий.

Пироэлектрики – класс веществ, обладающих спонтанной поляризацией, т.е. электрическим дипольным моментом в отсутствие электрического поля.

Основные свойства сегнетоэлектриков:

1) диэлектрическая проницаемость их гораздо больше единицы e>>1;

2) диэлектрическая проницаемость сегнетоэлектриков зависит от напряженности внешнего электрического поля;

3) во внешнем электрическом поле сегнетоэлектрики поляризуются до насыщения;

4) во внешнем циклически изменяющемся электрическом поле ему присуще явление гистерезиса, сложная зависимость вектора поляризации от напряженности электрического поля;

5) по своему строению сегнетоэлектрики представляют скопление областей спонтанной поляризации - доменов, электрические дипольные моменты которых имеют хаотические ориентации;

6) при нагревании сегнетоэлектриков до определенной температуры Т_к, они теряют все свои специфические свойства и превращаются в обычные полярные диэлектрики. Точка фазового перехода из состояния сегнетоэлектрика в состояние полярного диэлектрика называется точкой Кюри, а соответствующая ей температура Т_к - температурой Кюри.

Закон изменения диэлектрической восприимчивости c вблизи температуры Кюри (закон Кюри-Вейса) имеет вид

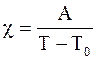, (3.74)

где А – некоторая константа;

T₀ – температура Кюри-Вейса, близкая к температуре Кюри T_к.

Пьезоэлектрики – сегнетоэлектрики, у которых возникают перераспределение электрических зарядов при деформации в отсутствие электрического поля.

Прямой пьезоэлектрический эффект – процесс возникновения электрических зарядов в отсутствие электрического поля при деформации пьезоэлектрика.

Обратный пьезоэлектрический эффект – процесс появления механических деформаций у пьезоэлектрика под влиянием электрического поля.

Прямой пироэлектрический эффект – процесс появления электрических зарядов при изменении температуры пироэлектрика.

Обратный пироэлектрический эффект (электрокалорический эффект) – изменение температуры пироэлектрика под влиянием электрического поля.

Электреты – диэлектрики, которые длительное время сохраняют поляризованное состояние после снятия внешнего воздействия.

3.4. Энергия электрического поля

Энергия взаимодействия электрических зарядов

, (3.75)

где j_i – потенциал, создаваемый всеми зарядами, кроме i-го, в точке нахождения заряда q.

Энергия заряженного конденсатора (системы заряженных проводников)

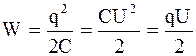. (3.76)

Дата добавления: 2014-12-07