Ранг и дефект линейного оператора

Для доказательства основной теоремы этого параграфа потребуется понятие прямой суммы подпространств.

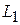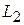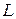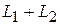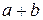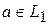Пусть и – два подпространства линейного пространства . Их суммой называется множество всех векторов , где и 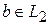, т.е.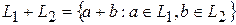

Легко проверить, что 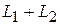также будет подпространством L.

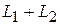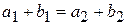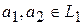Сумма называется прямой, если из того, что , где и 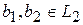следует, что 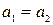и .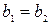

Определим также и пересечение двух подпространств 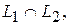которое также будет подпространством 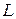. Именно

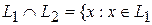и

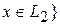
ТЕОРЕМА (о прямых суммах подпространств). Сумма подпространств 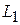и 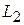будет прямой тогда и только тогда, когда .

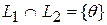ДОКАЗАТЕЛЬСТВО. Пусть 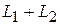– прямая сумма подпространств 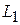и 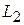, но есть вектор 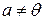такой, что 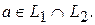Тогда, так как 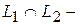также является подпространством, то 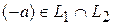, и получается, что нулевой вектор можно представить двумя различными способами 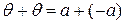. Таким образом, приходим к противоречию определения прямой суммы.

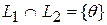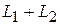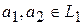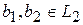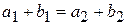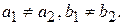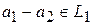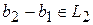Обратно, пусть , но сумма не прямая. Значит найдется и такие, что , но Так как и , то 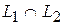содержит ненулевой вектор 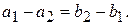Опять приходим к противоречию. □

ТЕОРЕМА (о размерности суммы двух подпространств). Размерность суммы двух подпространств пространства 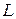равна сумме их размерностей минус размерность их пересечения.

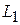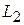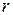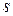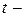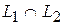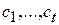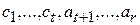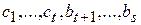ДОКАЗАТЕЛЬСТВО. Пусть и – подпространства, и их размерности, а размерность их пересечения. Рассмотрим некоторый базис , скажем , и дополним его до базисов и пространств 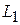и .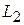

Докажем, что система

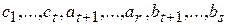, (3)

состоящая из 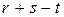векторов является базисом подпространства 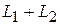, тем самым будет доказана и теорема.

Ясно, что любой вектор 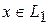и 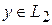, а значит и вектор 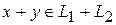линейно выражается через векторы системы (3), т.к. содержит базисы 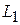и 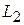. Осталось проверить, что система (3) линейно независима. Предположим, что

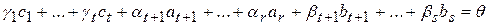(4)

Пусть 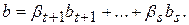Понятно, что 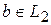. Но

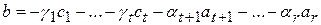. (5)

Правая часть этого равенства есть вектор из 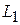, т.е. 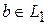. Окончательно, 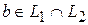. Значит в выражении (5) отсутствуют члены с 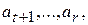т.е. 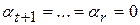. Отсюда и из (4) заключаем, что

.

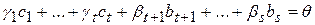Так как система 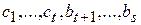является базисом 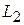, то она линейно независима и поэтому □

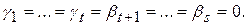Если сумма 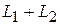прямая, то размерность 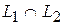по теореме о прямых суммах равна 0, и поэтому получаем

СЛЕДСТВИЕ. Размерность прямой суммы двух подпространств равна сумме их размерностей. □

Пусть 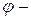линейный оператор 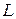и

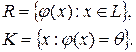
Нетрудно проверить, что и подпространства 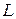, называемые областью значений и ядром линейного оператора 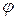. Размерность называется рангом, а размерность 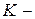дефектом .

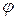ТЕОРЕМА (о ранге и дефекте). Сумма ранга и дефекта линейного оператора φ равна размерности пространства .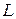

ДОКАЗАТНЛЬСТВО. Пусть 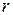и 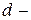ранг и дефект 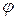. Выберем в базис 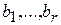и обозначим через 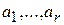векторы такие, что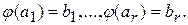

Они линейно независимы, т.к. из равенства 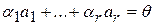следует, что 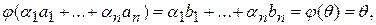а поскольку 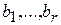линейно независимы, то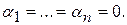

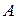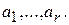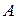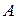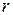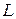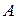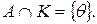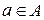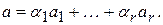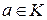Обозначим через подпространство, порожденное векторами Они образуют базис и поэтому размерность подпространства равна . По предыдущему следствию достаточно теперь доказать, что является прямой суммой и . покажем, что Любой вектор имеет вид Если , то 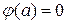, т.е. 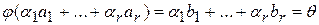. Но векторы 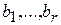линейно независимы и поэтому 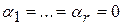, откуда .

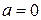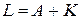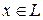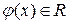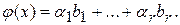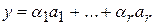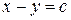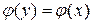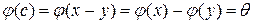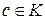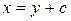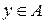Покажем теперь, что . Возьмем вектор . Но и поэтому Пусть и . Так как , то . Следовательно . Имеем , где и 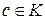, что и требовалось доказать. □

Дата добавления: 2014-11-29