Ранг матриц

Наивысший порядок минора матрицы, неравного нулю, называется минорным рангом матрицы.

Будем смотреть на столбцы, впрочем, как и на строки, матрицы 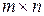как на векторы пространства 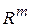(соответственно, 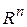). Говорят, что подмножество векторов 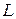линейного пространства является его подпространством, если для всех 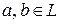и числа 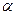выполнены два условия:

(а) ;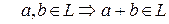

(б) .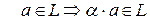

Их можно объединить в одно: для любых 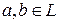и чисел 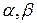вектор 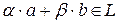. В этом случае нетрудно проверить выполнение всех свойств 1-8 сложения и умножения числа на вектор из § 2.1. Поэтому подпространства в свою очередь являются пространствами, т.к. условия 1-8 фактически являются аксиомами «быть пространством» для множества элементов 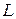, в котором заданы операции сложения и умножения числа на элемент из .

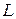Универсальным способом получения подпространств является следующий: надо взять произвольное множество 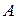векторов из пространства и тогда, как не трудно проверить, множество 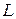всевозможных линейных комбинаций векторов из 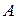образует подпространство исходного линейного пространства, о котором говорят, что оно порождено векторами 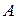. По теореме о базисах любая максимальная линейная независимая система векторов из 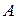содержит одно и то же число векторов. Поэтому корректно следующее определение: число столбцов, образующих в матрице максимальную линейно независимую систему, называется рангом матрицы по столбцам. Аналогично определяется и ранг матрицы по строкам.

ТЕОРЕМА (о ранге матриц). Ранг матрицы по столбцам равен ее минорному рангу.

ДОКАЗАТЕЛЬСТВО. Если в матрице любые 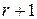столбцов линейно зависимы, то, по свойству 8 определителя, любой минор 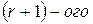порядка равен нулю. Поэтому минорный ранг не больше ранга по столбцам.

Обратно, пусть минорный ранг матрицы 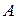порядка 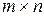равен 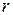. Так как при расстановке строк и столбцов матрицы ее ранг не меняется, то можно считать, что минор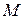 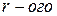порядка, не равный 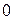, находится на пересечении первых 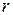столбцов и строк. Рассмотрим «окаймляющий» его минор.

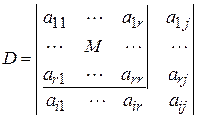
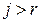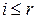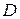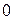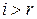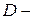Здесь . Если , то содержит две равные строки и, по свойству 4 определителей, равен . Если же , то минор 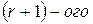порядка и равен 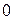по предположению. Вычислим 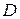методом разложения по последней строке:

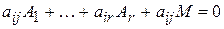(6)

Заметим, что 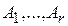, 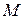не зависят от 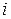. Из равенства (6) получаем:

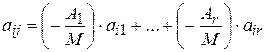
Это равенство справедливо при любом 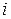. Поэтому 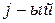столбец исходной матрицы равен линейной комбинации ее первых 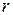столбцов, взятых с коэффициентами:

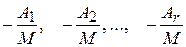
Итак, первые 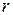столбцов образуют максимальную линейную независимую систему столбцов. Значит ранг по столбцам не выше минорного ранга, что заканчивает доказательство теоремы. □

Так как при транспонировании матрицы ее минорный ранг не меняется, то получаем:

СЛЕДСТВИЕ 5. Ранг матрицы по строкам равен ее рангу по столбцам. □

СЛЕДСТВИЕ 6. Квадратная матрица является невырожденной тогда и только тогда, когда ее строки (столбцы) образуют линейно независимую систему строк (столбцов). □

Доказательство теоремы о ранге дает и метод вычисления ранга матрицы. Именно, найдя минор 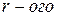порядка, не равный 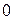, надо перебрать все его окаймляющие (в теореме надо брать 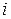, 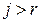), и, если все они равны 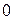, то ранг матрицы равен .

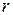Она дает также и способ нахождения максимальной линейно независимой системы строк (столбцов) матрицы. Именно, это будут те строки (столбцы), в которых лежит минор наивысшего порядка, не равный нулю.

Пример 1. Найти ранг матрицы

.

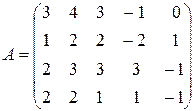Решение. Минор второго порядка, стоящий в левом верхнем углу этой матрицы отличен от нуля.

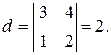
Минор третьего порядка

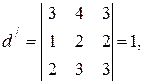
окаймляющий 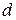, отличен от нуля, однако оба минора четвёртого порядка, окаймляющие 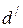, равны нулю:

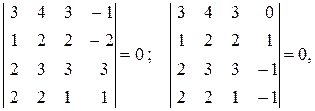
т. е. ранг матрицы 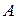равен трём.

Назовём элементарными следующие преобразования матриц:

- перестановка строк (столбцов);

- домножение строки (столбца) на число, отличное от нуля;

- добавление к одной строке (столбцу) другой строки (столбца), умноженной на некоторое число;

- вычёркивание нулевой строки (столбца).

УТВЕРЖДЕНИЕ 1. Элементарные преобразования не меняют ранга матрицы. □

УТВЕРЖДЕНИЕ 2. Система из 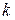векторов

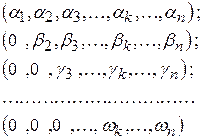
линейно независима. □

В заключении укажем ещё один алгоритм нахождения ранга матриц, основанный на утв. 1, 2: с помощью элементарных преобразований приведём матрицу к ступенчатому виду; количество её строк и будет рангом матрицы.

Пример 2. Найти ранг матрицы

.

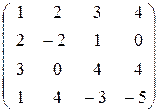Решение. Домножим первую строку матрицы на (-2), (-3), (-1) и прибавим, соответственно, ко второй, третьей и четвёртой строкам, получим

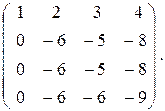
Теперь домножим вторую строку матрицы на (-1) и прибавим к третьей и четвёртой строкам. Вычеркнув нулевую строку, получим матрицу

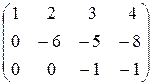
ступенчатого вида, у которой три строки. Т. е. ранг матрицы равен трём.

Дата добавления: 2014-11-29