Теоремы о произведении определителей и обратной матрице. Правило Крамера

Пример 5.

Для вычисления определителей более высоких порядков пользуются следующим алгоритмом: с помощью свойства 9 определителей добиваются того, чтобы в одной строке (или в одном столбце) все элементы за исключением одного равнялись нулю, затем по следствию 1 из теоремы Лапласа расписывают определитель по этой строке (столбцу). Тем самым вычисление определителя 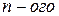сводят к вычислению определителя порядка. При необходимости процедуру повторяют.

Пример 6. Вычислить определитель

.

Решение. Домножив первую строку на (-2), (-1), (-2) и добавляя её соответственно ко второй, третьей и четвёртой строке, получим

Распишем определитель по первому столбцу:

.

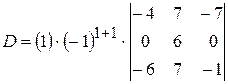Расписывая полученный определитель третьего порядка по второй строке, получим

ТЕОРЕМА (о произведении определителей). Определитель произведения двух квадратных матриц 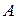и 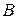одного и того же порядка равен произведению их определителей, т.е.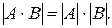

ДОКАЗАТЕЛЬСТВО. Рассмотрим вспомогательный определитель порядка

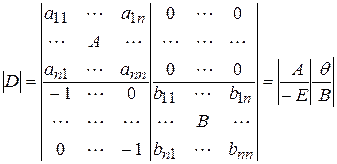
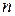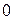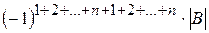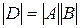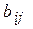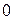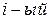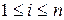Используя теорему Лапласа, вычислим , разлагая его по первым строкам. Так как в них лишь один минор может быть не равен , а его алгебраическое дополнение есть , то . Используя свойство 9 определителей, добьемся, что все элементы обратились в . Для этого столбец умножим на и прибавим к столбцу , и так для каждых и 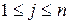. Получим

Вычислим , разлагая его по последним 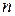столбцам. Получим , где .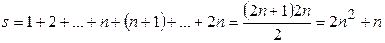

Тогда и . Но нетрудно проверить, что . □

Пусть 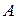и 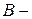матрицы порядка 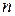. Матрица 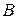называется обратной для матрицы 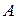, если 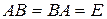. Матрица 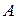называется невырожденной, если .

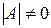ЛЕММА (к теореме об обратной матрице).

(а) если 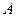имеет обратную матрицу 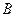, то 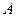- невырожденная;

(б) если обратная матрица для 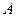существует, то она единственна.

ДОКАЗАТЕЛЬСТВО.

(а) Имеем . По теореме о произведении определителей получаем 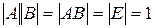. Значит .

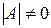(б) Пусть 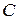также обратная матрица для 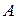. Используя ассоциативность умножения матриц, имеем . □

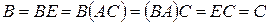Оказывается утверждение (а) можно обратить.

ТЕОРЕМА (об обратной матрице). Если матрица 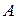- невырожденная матрица, то она имеет обратную матрицу 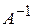, где

(4)

Иными словами, 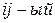элемент 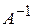равен алгебраическому дополнению элемента 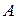, деленному на .

ДОКАЗАТЕЛЬСТВО. Найдем 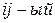элемент произведения матрицы 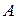на указанную матрицу 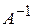(4). Он равен

.

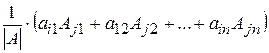Но по следствиям 1 и 2 из теоремы Лапласа сумма в скобках равна , если 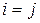, и равна 0, если 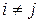. Следовательно . Аналогично, используя замечание после следствия 2, доказывается, что . □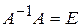

Дата добавления: 2014-11-29