
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ответы
ЗАДАЧИ К ГЛАВЕ IV.
Вычислить выражения:
133. 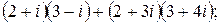
134. 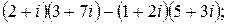
135. 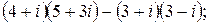
136. 
137. 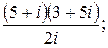
138. 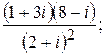
139. 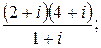
140. 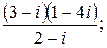
141. 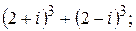
142. 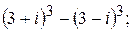
143. 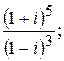
144. 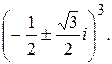
145. Вычислить 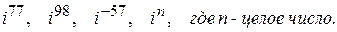
Решить уравнения:
146. 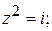
147. 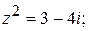
148. 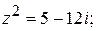
149. 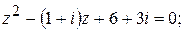
150. 
151. 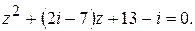
Найти тригонометрическую форму комплексных чисел:
152. 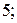
153. 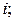
154. 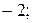
155. 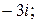
156. 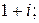
157. 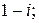
158. 
159. 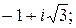
160. 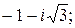
161. 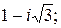
162. 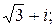
163. 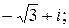
164. 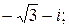
165. 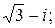
166. 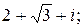
167. 
Вычислить выражения:
168. 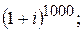
169. 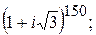
170. 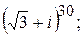
171. 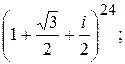
172. 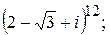
173. 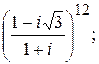
174. 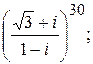
175. 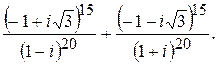
Решить уравнения:
176. 
177. 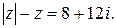
При 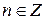 вычислить выражения:
вычислить выражения:
178. 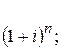
179. 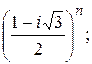
180. Доказать, что если комплексное число 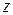 является одним из корней степени
является одним из корней степени 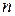 из вещественного числа
из вещественного числа 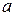 , то и сопряжённое число
, то и сопряжённое число 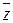 является одним из корней степени
является одним из корней степени 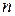 из
из 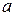 .
.
Вычислить:
181. 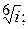
182. 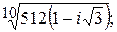
183. 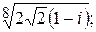
184. 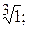
185. 
186. 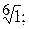
187. 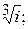
188. 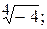
189. 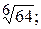
190. 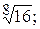
191. 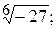
192. 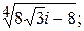
193. 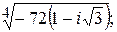
194. 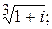
195. 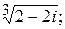
196. 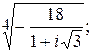
197. 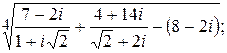
198. 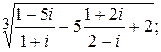
199. 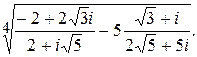
Решить уравнения:
200. 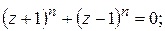
201. 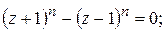
202. 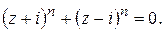
203. Найти произведение всех корней степени 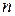 из единицы.
из единицы.
Используя алгоритм Евклида, Разделить многочлен 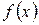 с остатком на многочлен
с остатком на многочлен 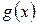 :
:
204. 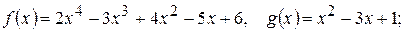
205. 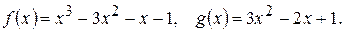
Найти наибольший общий делитель многочленов 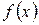 и
и 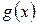 :
:
206. 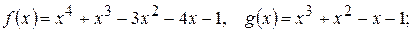
207. 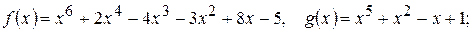
208. 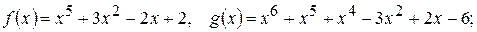
209. 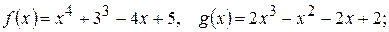
210. 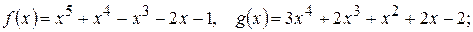
211. 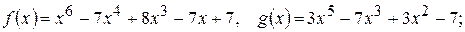
212. 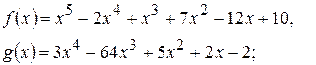
213. 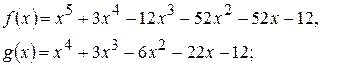
214. 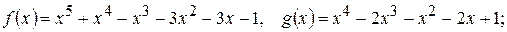
215. 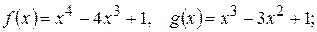
216. 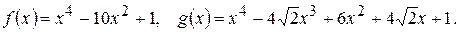
Найти наибольший общий делитель многочленов 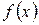 и
и 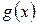 и его линейное выражение через
и его линейное выражение через 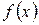 и
и 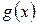 :
:
217. 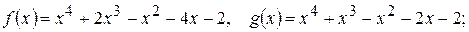
218. 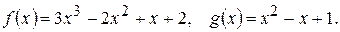
1. 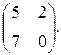
2. 
3. 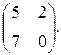
4. 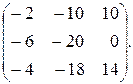
5. 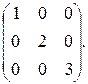
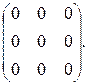
6. 
7. 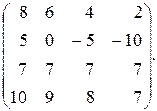
8. 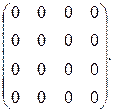
9. 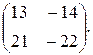
10. 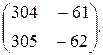
11. 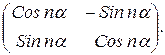
12. 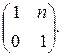
13. 
14. 1.
15. -2.
16. 0.
17. 0.
18. 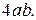
19. 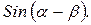
20. 0.
21. 0.
22. 1.
23. 40.
24. -10.
25. 180.
26. 87.
27. 0.
28. 10.
29. -8.
30. -3.
31. -9.
32. 18.
33. 18.
34. 17.
35. -6.
36. -10.
37. 100.
38. 150.
39. 52.
40. 5.
41. 10.
42. 1.
43. 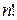
44. 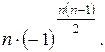
45. 0.
46. 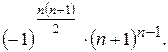
47. 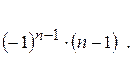
48. 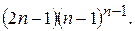
49. 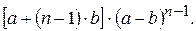
50. 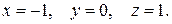
51. 
52. 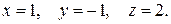
53. 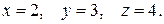
54. 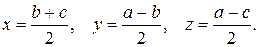
55. 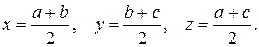
56. 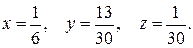
57. 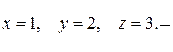
58. 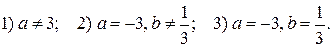
59. 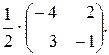
60. 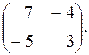
61. 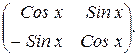
62. 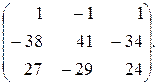
63. 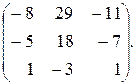
64. 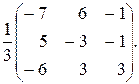
65. 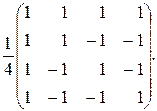
66. 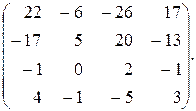
67. 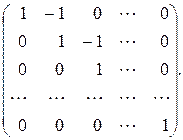
68. 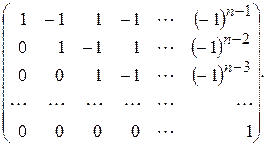
69. 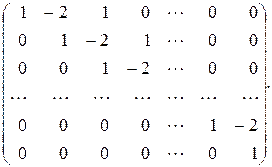
70. 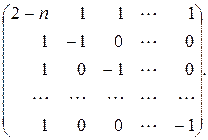
71. 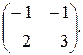
72. 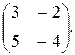
73. 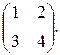
74. 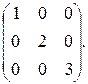
75. 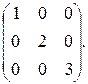
76. 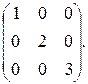
77. 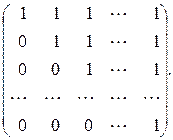
78. 2.
79. 3.
80. 3.
81. 2.
82. 2.
83. 2.
84. 3.
85. 3.
86. 2.
87. При 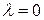 ранг матрицы равен 2, при
ранг матрицы равен 2, при 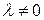 ранг равен 3.
ранг равен 3.
88. При 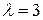 ранг матрицы равен 2, при
ранг матрицы равен 2, при 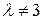 ранг равен 3.
ранг равен 3.
89. Общее решение, например:
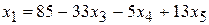 ,
, 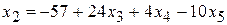 ; частное решение:
; частное решение: 
90. Общее решение:
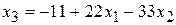 ,
, 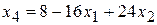 ; частное решение:
; частное решение: 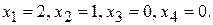
91. Общее решение:
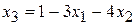 ,
, 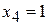 ; частное решение:
; частное решение: 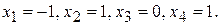
92. Общее решение: 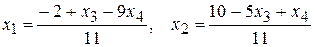 ; частное решение:
; частное решение: 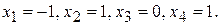
93. Система несовместна.
94. Система имеет единственное решение: 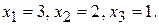
95. Система несовместна.
96. Общее решение: 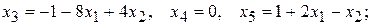 частное решение:
частное решение: 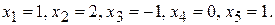
97. Общее решение: 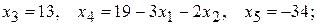 частное решение:
частное решение: 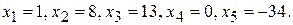
98. Система имеет единственное решение: 
99. Система несовместна.
100. При 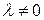 система несовместна. При
система несовместна. При 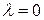 она совместна, и общее решение имеет вид:
она совместна, и общее решение имеет вид: 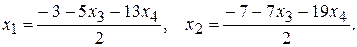
101. Система совместна при любых значениях 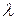 . При
. При 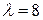 общее решение имеет вид:
общее решение имеет вид: 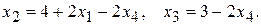 При
При 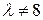 общее решение имеет вид:
общее решение имеет вид: 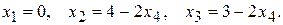
102. Общее решение, например: 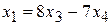 ,
, 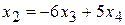 . Фундаментальная система решений:
. Фундаментальная система решений:
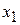
| 
| 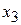
| 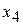
|
| -6 | |||
| -7 |
103. Общее решение: 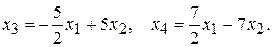 Фундаментальная система решений:
Фундаментальная система решений:
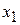
| 
| 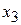
| 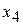
|
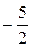
| 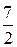
| ||
104. Система имеет только нулевое решение.
105. Система имеет только нулевое решение.
106. Общее решение: 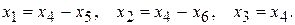 Фундаментальная система решений:
Фундаментальная система решений:
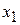
| 
| 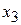
| 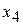
| 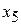
| 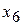
|
| -1 | |||||
| -1 |
107. Общее решение: 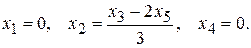 Фундаментальная система решений:
Фундаментальная система решений:
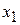
| 
| 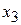
| 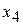
| 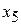
|
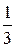
| ||||
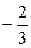
|
108. Общее решение: 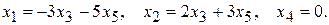 Фундаментальная система решений:
Фундаментальная система решений:
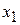
| 
| 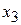
| 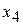
| 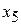
|
| -3 | ||||
| -5 |
109. Четвёртая строка вместе с любыми двумя из первых трёх строк образуют фундаментальную систему, а остальные системы строк - не образуют.
110. 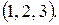
111. 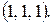
112. 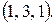
113. 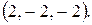
114. 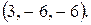
115. 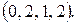
116. 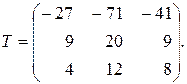
117. 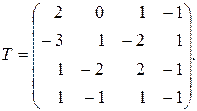
118. 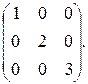
119. 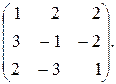
120. а) 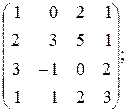
б) 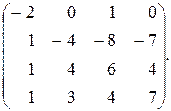
121. Собственные значения: 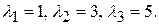 Соответствующие собственные векторы:
Соответствующие собственные векторы: 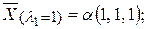
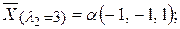
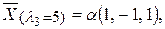 где
где 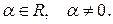
122. Собственные значения: 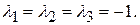 Собственные векторы имеют вид:
Собственные векторы имеют вид: 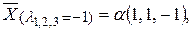 где
где 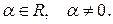
123. Собственные значения: 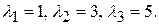 Соответствующие собственные векторы:
Соответствующие собственные векторы: 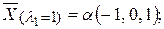
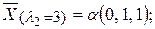
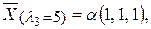 где
где 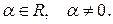
124. Собственные значения: 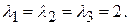 Собственные векторы имеют вид:
Собственные векторы имеют вид: 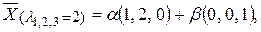 где
где 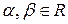 и
и 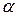 и
и 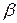 не равны нулю одновременно.
не равны нулю одновременно.
125. Собственные значения: 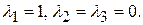 Соответствующие собственные векторы:
Соответствующие собственные векторы: 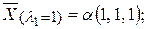
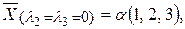 где
где 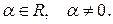
126. Собственные значения: 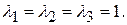 Собственные векторы имеют вид:
Собственные векторы имеют вид: 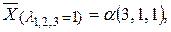 где
где 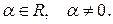
127. Собственные значения: 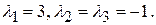 Соответствующие собственные векторы:
Соответствующие собственные векторы: 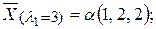
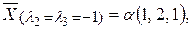 где
где 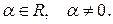
128. Собственные значения: 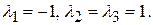 Соответствующие собственные векторы:
Соответствующие собственные векторы: 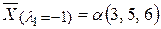 , где
, где 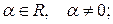
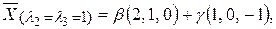 где
где 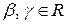 и
и 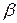 и
и 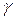 не равны нулю одновременно.
не равны нулю одновременно.
129. Собственные значения: 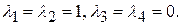 Соответствующие собственные векторы:
Соответствующие собственные векторы: 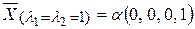 , где
, где 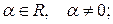
 где
где 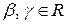 и
и 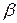 и
и 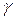 не равны нулю одновременно.
не равны нулю одновременно.
130. Собственные значения: 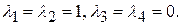 Соответствующие собственные векторы:
Соответствующие собственные векторы: 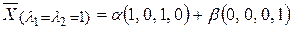 , где
, где 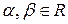 и
и 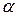 и
и 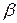 не равны нулю одновременно;
не равны нулю одновременно; 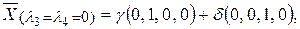 где
где 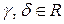 и
и 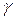 и
и 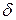 не равны нулю одновременно.
не равны нулю одновременно.
131. Собственные значения: 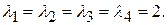 Собственные векторы имеют вид:
Собственные векторы имеют вид: 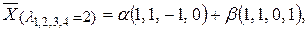 где
где 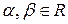 и
и 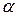 и
и 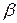 не равны нулю одновременно.
не равны нулю одновременно.
132. Собственные значения: 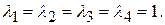 Собственные векторы имеют вид:
Собственные векторы имеют вид: 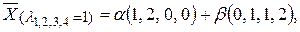 где
где 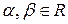 и
и 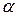 и
и 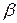 не равны нулю одновременно.
не равны нулю одновременно.
133. 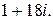
134. 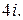
135. 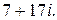
136. 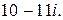
137. 
138. 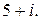
139. 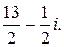
140. 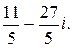
141. 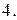
142. 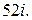
143. 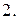
144. 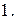
145. 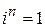 при
при 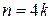 ,
, 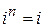 при
при  ,
, 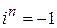 при
при 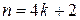 ,
, 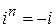 при
при 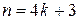 , где
, где 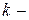 целое число;
целое число; 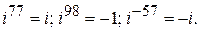
146. 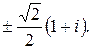
147. 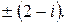
148. 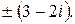
149. 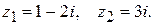
150. 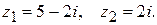
151. 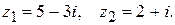
152. 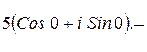
153. 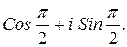
154. 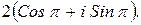
155. 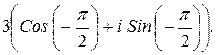
156. 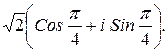
157. 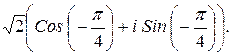
158. 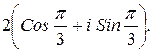
159. 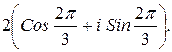
160. 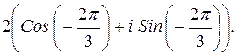
161. 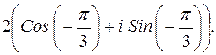
162. 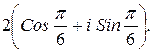
163. 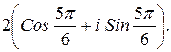
164. 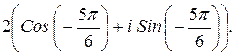
165. 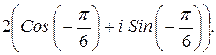
166. 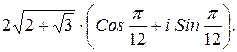
167. 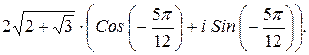
168. 
169. 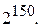
170. 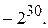
171. 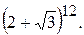
172. 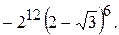
173. 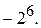
174. 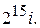
175. 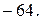
176. 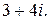
177. 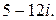
181. 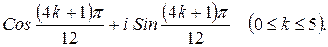
182. 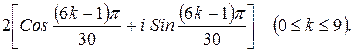
183. 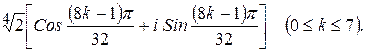
184. 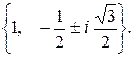
185. 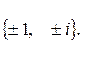
186. 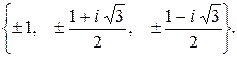
187. 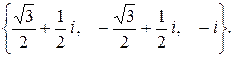
188. 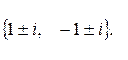
189. 
190. 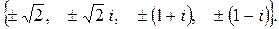
191. 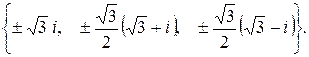
192. 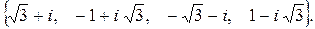
193. 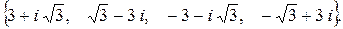
194. 
195. 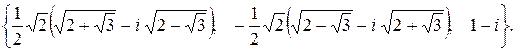
196. 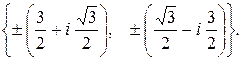
197. 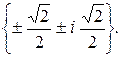
198. 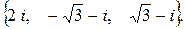
199. 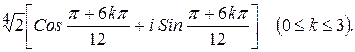
203. 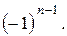
204. 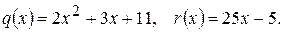
205. 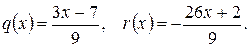
206. 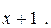
207. 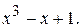
208. 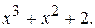
209. 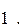
210. 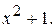
211. 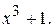
212. 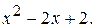
213. 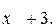
214. 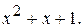
215. 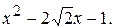
216. 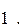
217. 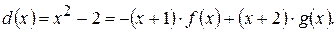
218. 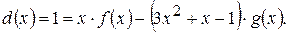
СПИСОК ЛИТЕРАТУРЫ.
1. Ильин В. А., Позняк Э. Г. Линейная алгебра: Учеб.: Для ВУЗов. - М.: Физматлит, 2001.
2. Курош А. Г. Курс высшей алгебры. - М.: Наука, 1971.
3. Проскуряков И. В. Сборник задач по линейной алгебре. - М.: Наука, 1984.
4. Шипачёв В. С. Задачник повысшей математике: Учеб. пособие для ВУЗов. - М.: Высшая школа, 2002.
СОДЕРЖАНИЕ.
ВВЕДЕНИЕ. ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ. 3
ГЛАВА I. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ. 5
§1.1. Матрицы и операции над ними. 5
§1.2. Определители. Теорема Лапласа. 8
§1.3. Теоремы о произведении определителей и обратной
матрице. Правило Крамера. 14
ЗАДАЧИ К ГЛАВЕ I. 19
ГЛАВА II. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И СИСТЕМЫ
ЛИНЕЙНЫХ УРАВНЕНИЙ. 25
§2.1. Арифметическое линейное пространство 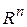 . 25
. 25
§2.2. Ранг матриц. 30
§2.3. Системы линейных уравнений. 34
ЗАДАЧИ К ГЛАВЕ II. 41
ГЛАВА 3. ЛИНЕЙНЫЕ ОПЕРАТОРЫ. 45
§3.1. Матрицы линейных операторов. 45
§3.2. Ранг и дефект линейного оператора. 51
§3.3. Характеристические корни и собственные значения. 54
ЗАДАЧИ К ГЛАВЕ III. 60
ГЛАВА 4. ОСНОВНЫЕ АЛГЕБРАИЧЕСКИЕ СТРУКТУРЫ. 63
§4.1. Группы, кольца, поля. 63
§4.2. Поле комплексных чисел. 67
§4.3. Поля вычетов. 73
§4.4. Кольца многочленов. 75
ЗАДАЧИ К ГЛАВЕ IV. 89
ОТВЕТЫ. 92
СПИСОК ЛИТЕРАТУРЫ. 100
СОДЕРЖАНИЕ. 101
Дмитрий Иванович Иванов
АЛГЕБРА
(часть I)
Учебно-методическое пособие
по дисциплине "Алгебра"
для студентов специальности
"Компьютерная безопасность"
|
|
Дата добавления: 2014-11-29; Просмотров: 442; Нарушение авторских прав?; Мы поможем в написании вашей работы!