Формула Релея-Джинса

Стоячие волны в трехмерном пространстве.

Чтобы определить число нормальных мод с частотами в интервале от 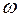до 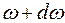в трехмерном пространстве, обратимся сначала к рассмотренной ранее задаче о нормальных колебаниях в струне с закрепленными концами, для которой было установлено, что нормальные колебания представляют собой стоячие волны, описываемые уравнением

,

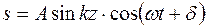где волновые числа 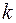определяются граничными условиями .

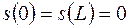Первое условие выполняется автоматически для данной функции, описывающей распределение амплитуды вдоль струны. Из второго условия следует 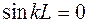, т.е

, .

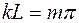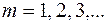В одномерной структуре с такими граничными условиями волновые числа образуют бесконечное счетное множество

, .

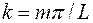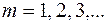Представления о нормальных колебаниях можно обобщить на двумерные и трехмерные структуры. В случае квадратной мембраны с закрепленными краями нормальные колебания также представляют собой стоячие волны, описываемые уравнением

.

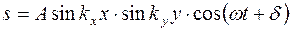Первые два сомножителя описывают распределение амплитуды по мембране, а последний - колебательный процесс.

Проекции волнового вектора на оси координат здесь также определяются граничными условиями и образуют бесконечные счетные множества

, ,

, .

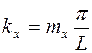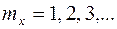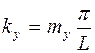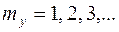По аналогии можно записать уравнение нормальных колебаний в объемном резонаторе в форме куба с ребром L

,

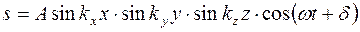где

, ,

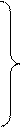
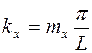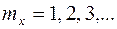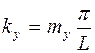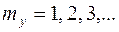, , (2)

, .

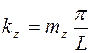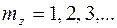Для электромагнитных колебаний в полости нормальные колебания также представляют собой стоячие волны. Из опыта следует, что равновесное тепловое излучение не зависит ни от формы полости, ни от материала ее стенок. Поэтому для упрощения дальнейших рассуждений выберем полость в виде куба с длиной ребра L с идеально проводящими стенками. Последнее означает, что граничные условия для потенциала электрического поля являются нулевыми.

В этом случае распределение потенциала в объеме куба можно описать выражением

,

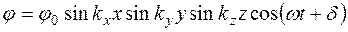где проекции волнового вектора на оси координат - k _x, k _y, k _z определяются по формулам (2). Они связаны с частотой колебаний соотношением

.

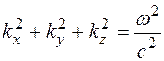Таким образом, нормальные колебания в полости характеризуются дискретным набором проекций волнового вектора на оси координат

, , .

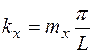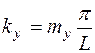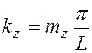Каждой тройке чисел m _x, m _y, m _z соответствуют две волны с ортогональной поляризацией.

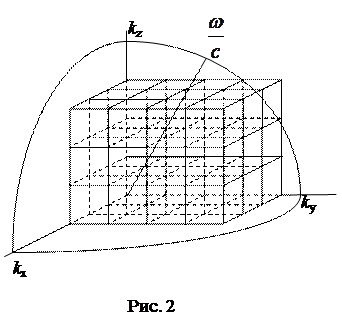Введем пространство волновых векторов с прямоугольными координатами k _x, k _y, k _z. В этом пространстве каждой стоячей волне (каждой тройке чисел m _x, m _y, m _z) будет соответствовать одна изображающая точка (рис. 2). Все изображающие точки расположатся в узлах кубической решетки. Элементарная ячейка этой решетки представляет кубик с ребром (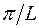) и объемом

.

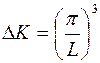На каждую такую ячейку приходится одна изображающая точка, так как у куба восемь вершин, но каждая вершина принадлежит восьми соприкасающимся ячейкам

Решетка заполняет только один октант пространства волновых векторов. Проведем из начала координат сферу радиусом 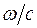. Объем части шара в одном октанте равен

,

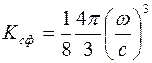а число изображающих точек, попавших в эту сферу, получим, если этот объем разделим на объем элементарной ячейки. Учитывая, что каждой изображающей точке соответствуют два нормальных колебания с разной поляризацией, получим, что число различных нормальных колебаний, частоты которых не превышают w, равно

,

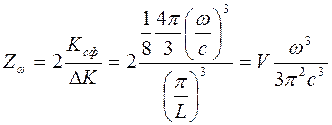где V – объем полости.

Продифференцировав это соотношение, получим

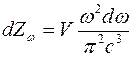. (3)

Подставив (3) в (1) найдем выражение для спектральной объемной плотности энергии

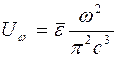. (4)

В классической статистической физике для средней энергии 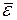, приходящейся на одну колебательную степень свободы, получена формула

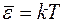. (5)

Поэтому для спектральной объемной плотности энергии 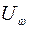запишем выражения

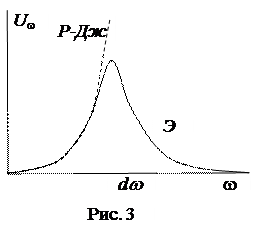
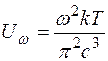, (6)

Эта формула называется формулой Релея-Джинса для теплового излучения.

На рис. 3 приведены экспериментальная (Э) и теоретическая (Р-Дж) зависимости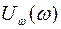

В области малых частот формула Релея-Джинса дает совпадающие с экспериментом результаты, а в области больших частот (фиолетовая, ультрафиолетовая и рентгеновская часть спектра) теория дает сильно завышенные результаты. Это приводит к тому, что теоретическое значение объемной плотности энергии электромагнитного поля

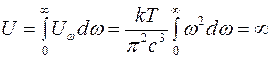
обращается в бесконечность, что означает, что все тела должны мгновенно отдавать свою энергию в излучение.

Данное расхождение теории и эксперимента П.С.Эренфест назвал ультрафиолетовой катастрофой.

Катастрофа заключается в том, что классическая физика не смогла объяснить, почему печка долго не остывает.

По теории Релея-Джинса тепловое равновесие между излучением и веществом невозможно. Причина ультрафиолетовой катастрофы состоит в том, что поле имеет бесконечно большое число степеней свободы, а вещество - конечное. Поэтому если бы было справедливо равномерное распределение энергии по степеням свободы, то при тепловом равновесии вся энергия должна была бы сосредоточиться в поле.

Дата добавления: 2014-11-29