Столкновение заряженных частиц

В опытах Резерфорда применялись очень тонкие металлические фольги с толщиной порядка 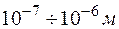. Это и позволяло не учитывать многократные столкновения 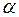-частиц с атомами металла. Вероятность таких столкновений ничтожно мала. Точно так же ничтожно мала вероятность рассеяния 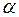-частиц на большие углы при столкновении с электронами в виду малости их масс.

Учитывая взаимодействие 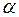-частицы только с ядром, к которому 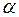-частица подходит наиболее близко мы приходим к задаче столкновения двух заряженных частиц.

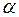Предположим, что -частица имея импульс 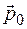, направленный вдоль прямой 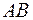приближается к неподвижному ядру. Сила взаимодействия двух частиц с зарядам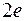и и 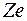по закону Кулона равна

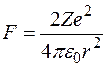
и является силой отталкивания. За счет отталкивания 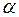-частица будет отклоняться от прямой 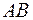и двигаться по гиперболической траектории., постепенно приближаясь к прямой 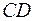. Прямые 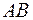и 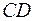являются асимптотами гиперболы, и, следовательно, являются касательными к траектории в бесконечно удаленных точках. Эти асимптоты пересекаются под углом 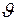. Угол 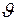называется углом рассеяния.

Проведем прямые 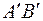и 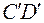через рассеивающий центр, помещенный в начало координат, параллельно соответствующим асимптотам. Расстояние между прямым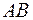и и 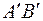называется прицельным параметром 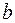. Оси координат выберем так, чтобы они являлись биссектрисами углов между прямым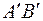и и 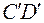. При движении 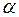-частицы угол 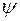, образованный радиус-вектором, проведенным от ядра к 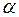-частице, и осью 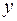изменяется от 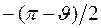до .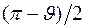

Так как сила взаимодействия является центральной, то момент силы равен нулю. Поэтому момент импульса при таком движении является постоянной величиной

.

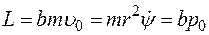Кроме того сохраняется полная энергия 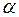-частицы

.

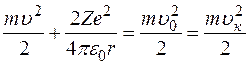Поэтому начальная и конечная скорости 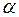-частицы одинаковы 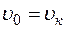, и, значит, одинаковы прицельные параметры для обеих асимптот.

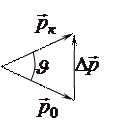На основании второго закона Ньютона изменение импульса 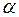-частицы при рассеянии на неподвижном ядре равно импульсу силы, действующей на 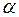-частицу

.

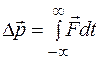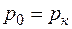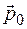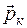Левая часть оттого уравнения легко вычисляется, так как и угол между векторами и равен :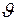

.

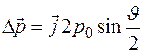В правой части представим 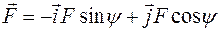и .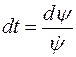

Таким образом,

.

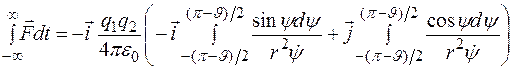На основании закона сохранения момента импульса величину

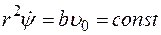
можно вынести из под интеграла и учесть, что 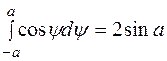и 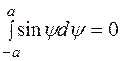. В результате получим

.

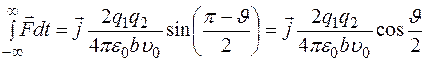Таким образом

.

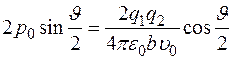Отсюда находим

.

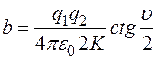Данное соотношение устанавливает связь прицельного параметра и угла рассеяния. При 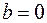получаем 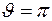. С увеличением прицельного параметра угол 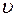уменьшается и при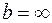 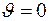. Следует отметить, что когда прицельный параметр становится больше радиуса атома, закон Кулона перестает быть справедливым, так как положительный заряд ядра нейтрализуется электронами.

Это значит, что при малых углах рассеяния, используемая модель столкновения, перестает быть справедливой.

Дата добавления: 2014-11-29