Понятие о квантах. Средняя энергия осциллятора. Фотоны

1. Формирование электромагнитного поля равновесного излучения является случайным процессом, так как случайны процессы испускания света телами. Поэтому энергия любого нормального колебания в равновесном излучении является случайной величиной. При определении ее среднего значения необходимо использовать закон Больцмана для распределения вероятности по состояниям.

По классическим представлениям энергия любой системы может изменяться на бесконечно малую величину, т.е. является непрерывной величиной. В этом случае закон Больцмана имеет вид

.

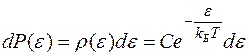Здесь 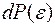- вероятность обнаружения системы в состоянии с энергией в пределах от 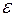до ,

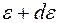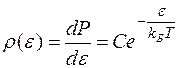- (7)

плотность распределения вероятности по энергии. С увеличением энергии вероятность обнаружения системы уменьшается по экспоненциальному закону.

Если в формуле (5) положить 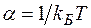и 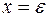, то нормировочная постоянная будет равна 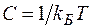, а

. (8)

Среднее значение энергии нормального колебания в равновесном излучении одинаково для любой моды, в соответствии с максвелловским принципом о равномерном распределении энергии по степеням свободы, и не зависит от частоты.

Таким образом, представление о том, что энергия любой системы принимает непрерывный ряд значений, приводит к закону Релея – Джинса.

2. Для объяснения своей эмпирической формулы, дающей правильное распределение энергии в спектре равновесного излучения, М.Планку пришлось предположить, что энергия осциллятора поля (нормального колебания) изменяется порциями – квантами и может принимать дискретный ряд значений 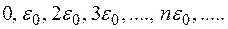. В этом случае вероятность обнаружения осциллятора поля в состоянии с энергией 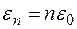описывается формулой

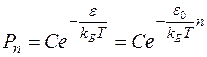. (9)

Если взять большое число одинаковых осцилляторов (ансамбль осцилляторов), то в соответствии с этим законом в состояниях с малой энергией будет находиться больше осцилляторов, чем в состояниях с большой энергией. Вероятность того, что осциллятор будет иметь бесконечно большую энергию, равна нулю.

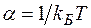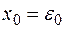Положив в формуле (2) и получаем

.

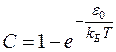При этом для среднего значения энергии осциллятора поля получается выражение

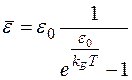. (10)

Данное выражение показывает, что средняя энергия осциллятора определяется квантом энергии и абсолютной температурой. При малых энергиях кванта 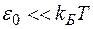среднее значение энергии моды совпадает с классическим 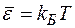. С увеличением энергии кванта среднее значение энергии моды стремится к нулю. Таким образом, дискретность энергии приводит к неравноправию степеней свободы. Моды с большим значением 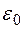обладают в среднем малой энергией, т.е. не возбуждаются.

Следовательно, чтобы изменить вид функции Релея-Джинса, необходимо считать, что величина кванта энергии является конечной величиной и должна зависеть от частоты осциллятора.

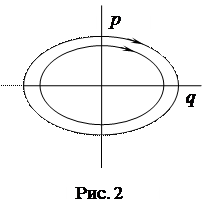3. Рассматривая энергию осциллятора и его фазовый портрет (рис. 2), мы установили, что энергия осциллятора равна произведению действия на частоту

.

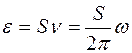Сопоставляя эту формулу с возможными по Планку значениями энергии осциллятора

,

приходим к выводу, что дискретным (квантованным) значениям энергии осциллятора должны соответствовать дискретные значения действия

. (11)

При этом для кванта энергии получаем формулу

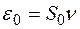. (12)

Из дискретности действия (11) следует, что на фазовой плоскости для осциллятора возможны не все фазовые траектории, а только такие, для которых площадь, ограниченная фазовой траекторией, кратна S ₀ (рис. 2). Величина S ₀ является квантом действия и называется постоянной М. Планка, для которой он ввел специальное обозначение .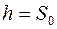

В теоретических исследованиях часто используют постоянную П. Дирака 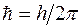и круговую частоту .

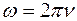В этих обозначениях выражение для кванта энергии записывается в виде

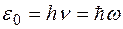. (13)

4. Таким образом, из гипотезы М. Планка получается, что средняя энергия осциллятора поля является функцией частоты и температуры

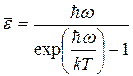. (14)

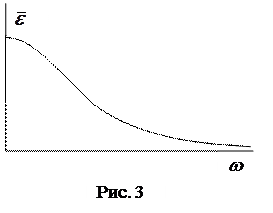
На рис. 3 показана зависимость 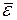от частоты для фиксированной температуры.

На малых частотах, когда квант энергии мал по сравнению со средней тепловой энергией молекул (), экспоненту можно разложить в ряд Тейлора и ограничиться первыми двумя слагаемыми

.

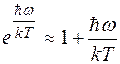Для таких низкочастотных осцилляторов средняя энергия (10) совпадает с классической

.

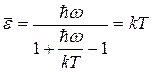На высоких частотах (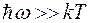), когда квант энергии много больше средней тепловой энергии атомов, единицей в знаменателе (10) можно пренебречь по сравнению с экспонентой

,

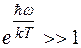и мы получаем, что средняя энергия осциллятора становится очень маленькой

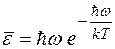. (15)

Физически это означает, что такие осцилляторы не возбуждаются и не принимают участия в формировании равновесного излучения: атомы не могут обеспечить значительное количество квантов с таким большим значением энергии. Осцилляторы есть, но тепловое движение атомов не может их возбудить. Квантование энергии осцилляторов уменьшает эффективное число осцилляторов, участвующих в формировании теплового равновесия.

Используя формулу (14) для средней энергии осциллятора и подставляя ее в формулу Релея-Джинса, получим формулу М. Планка для спектральной плотности объемной плотности энергии теплового излучения

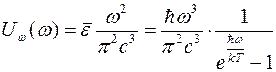. (16)

Данная формула позволила правильно объяснить все закономерности теплового излучения

5. Гипотеза М.Планка позволила не только дать правильное объяснение распределению энергии в спектре теплового излучения, но она позволила понять закономерности фотоэффекта и объяснить существование коротковолновой границы тормозного рентгеновского излучения.

При этом пришлось предположить, что свет не только излучается порциями, но и поглощается и распространяется в пространстве также порциями. В результате, в науке появилось представление о фотоне как о микрочастице света, обладающей как волновыми характеристиками: частотой 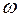и длиной волны 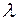, так и корпускулярными: энергией 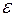и импульсом 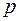, и движущейся в пространстве со скоростью света в вакууме .

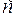Связь между частотой и энергией фотона дается формулой М.Планка

,

а связь между импульсом и длиной волны вытекает из релятивистского соотношения

.

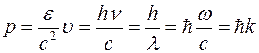Кроме того, для любой частицы, движущейся со скоростью 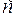, из уравнения 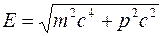следует 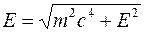, т.е. масса покоя такой частицы равна нулю .

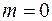Дата добавления: 2014-11-29