Принципы моделирования ионных кристаллов методом молекулярной динамики

Молекулярная динамика на графическом процессоре

Простейший алгоритм программы, реализующей моделирование ионных кристаллов (или других физических систем) методом молекулярной динамики, может быть представлен в форме, показанной на рис. 6.1.

Рис. 6.1. Блок-схема алгоритма молекулярной динамики

Заключается этот алгоритм в том, кристалл представляется системой недеформируемых, положительных и отрицательных, ионов, эволюционирующей во времени. Ионы перемещаются по законам Ньютона, а силы взаимодействия определяются парными потенциалами U_ij (R_ij).

Потенциалы U_ij (R_ij) имеют общий вид

,

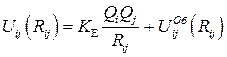где Q_i, Q_i, - заряды i -го и j -го ионов, R _ij – расстояние между этими ионами, K _E – константа закона Кулона, 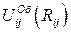- некулоновский потенциал взаимо­действия электроновских оболочек.

Потенциалы 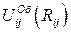представляют в различных формах, обычно включаю­щих в себя слагаемые, моделирующие отталкивание перекрываю­щихся электронных оболочек на малых расстояниях и дисперсионное притяжение на сравнительно больших. Наиболее известными из этих форм являются потенциал Букингема

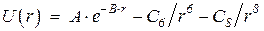
и потенциал Леннарда-Джонса

.

В формуле А и В – константы, характеризующие отталкивание оболо­чек, С ₆, С ₈ – константы, описывающие дипольную и квадрупольную со­ставляющие дисперсионного притяжения. В формуле e - глубина мини­мума потенциала, а s - положение его нуля.

Перед началом расчёта ионам присваиваются некоторые начальные коорди­наты и скорости (например - координаты, соответствующие узлам идеальной кристаллической решётки моделируемого соединения и скорости, соответ­ствующие Максвелловскому распределению при заданной температуре), после чего начинается численное пошаговое интегрирование уравнений движения ионов во времени. На каждом k -ом шаге производятся следующие действия:

· Рассчитываются действующие на каждый ион силы

;

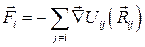· Вычисляются новые скорости и новые координаты ионов

.

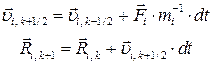Формулы - справедливы при нулевых граничных условиях (конеч­ный кристаллит из N частиц в вакууме) без компенсации перемещения, вращения и дрейфа температуры, возникающих из-за вычислительных погрешностей (алгоритмы компенсации приведены ниже). Однако этих формул достаточно, чтобы показать возможность эффективного распаралле­ливания по схеме SIMD: очевидно, что основные этапы алгоритма заклю­чаются в проведении над каждым из ионов поочерёдно одних и тех же операций.

Наиболее критичным участком алгоритма является расчёт результирующих сил, действующих на каждый из ионов со стороны остальных. Этот расчёт необходим на каждом шаге молекулярной динамики, а его объём квадра­тичен по количеству частиц N, так как для каждой из N частиц необходимо выполнить суммирование сил, действующих со стороны N-1 остальных:

.

Поскольку для реалистичного моделирования модельные кристаллиты должны содержать десятки и сотни тысяч ионов, объём расчёта очень велик по сравнению с расчётами на остальных этапах алгоритма. Именно этот расчёт имеет смысл в первую очередь реализовать на графических процессорах. Нам такая реализация позволила на порядки ускорить молеку­лярно-динамичес­кое моделирование ионных кристаллов (диоксида урана).

6.2. Программирование графического процессора для расчёта действующих на ионы результирующих сил

Расчёт сил, действующих на ионы в молекулярной динамике, мы рассмотрим на конкретном примере нашего решения этой задачи. Структура исходных данных и алгоритм получения результата в данном случае несколько более сложны, чем в предыдущем примере сложения матриц. Прежде, чем переходить к анализу текстов программ, опишем подробнее исходные данные и ожидаемый результат.

Дата добавления: 2014-12-07