Функция надежности

Будем называть элементом некоторое устройство независимо от того, «простое» оно или «сложное».

Пусть элемент начинает работать в момент времени 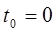, а по истечении времени длительностью 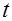происходит отказ. Обозначим через 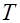непрерывную случайную величину – длительность времени безотказной работы элемента. Если элемент проработал безотказно (до наступления отказа) время, меньшее 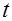, то, следовательно, за время – 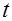наступит отказ.

Таким образом, функция распределения 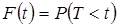определяет вероятность отказа за время – 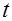. Следовательно, вероятность безотказной работы за это же время 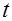, то есть вероятность противоположного события 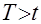равна

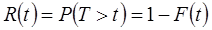. (21)

Функцией надежности 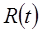называют функцию, определяющую вероятность безотказной работы элемента за время : .

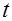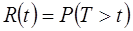Часто длительность времени безотказной работы элемента имеет показательное распределение, функция распределения которого

.

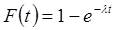Следовательно, в силу соотношения (41) функция надежности, в случае показательного распределения времени безотказной работы элемента, имеет вид:

.

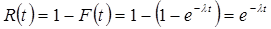Показательным законом надежности называют функцию надежности, определяемую равенством 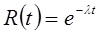, (22)

где 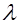– интенсивность отказов.

Как следует из определения функции надежности, эта формула позволяет найти вероятность безотказной работы элемента на интервале времени, длительностью 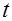, если время безотказной работы имеет показательное распределение.

Пример. Время безотказной работы элемента распределено по показательному закону 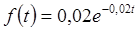, при 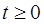( 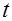– время). Найти вероятность того, что элемент работает безотказно 100 часов.

Решение. По условию, постоянная интенсивность отказов .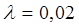

Тогда .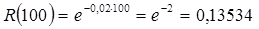

Искомая вероятность того, что элемент проработает безотказно 100 часов, приближенно равна 0,14.

Замечание. Если отказы элементов в случайные моменты времени образуют простейший поток, то вероятность того, что за время 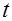не наступит ни одного отказа

.

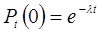Показательный закон надежности весьма прост и удобен для решения задач, возникающих на практике. Очень многие формулы теории надежности значительно упрощаются. Объясняется это тем, что этот закон обладает следующим важным свойством: вероятность безотказной работы элемента на интервале времени 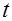не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени 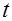(при заданной интенсивности отказов ).

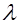Для доказательства свойства введем обозначения событий:

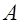– безотказная работа элемента на интервале 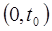длительностью ;

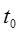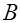– безотказная работа элемента на интервале 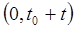длительностью .

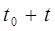Найдем вероятности этих событий: , ,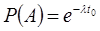

.

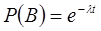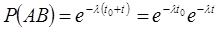Найдем условную вероятность того, что элемент будет работать безотказно на интервале 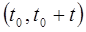при условии, что он уже проработал безотказно на предшествующем интервале :

.

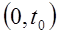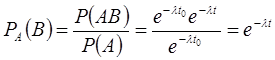Полученная формула не содержит 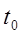, а содержит только 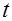. Это означает, что время работы на предшествующем интервале не сказывается на величине вероятности безотказной работы на последующем интервале, а зависит только от длины последующего интервала, что и требовалось доказать.

Полученный результат можно сформулировать несколько иначе. Сравнив вероятност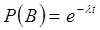и и 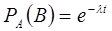, заключаем: условная вероятность безотказной работы элемента на интервале, длительностью 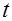, вычисленная в предположении, что элемент проработал безотказно на предшествующем интервале, равна безусловной вероятности.

Дата добавления: 2014-12-07