Свойства нормированного распределения Эрланга

1. Нормированное распределение Эрланга порядка 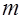описывает распределение среднего арифметического: ,

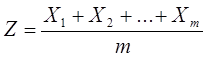где 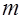независимых случайных величин, каждая из которых подчиняется показательному закону с одним и тем же параметром .

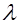2. Случайная величина , имеющая нормированное распределение Эрланга порядка 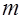, связана со случайной величиной 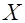, распределенной по закону Эрланга 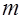-го порядка соотношением .

3. Нормированное распределение Эрланга порядка 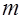описывает распределение суммы независимых случайных величин 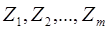, каждая из которых распределена по показательному закону с одним и тем же параметром .

Рис.7. Плотность вероятности нормированного распределения Эрланга

4. Сумма независимых случайных величин, имеющих нормированное распределение Эрланга порядка с одним и тем же параметром масштаба 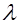имеет нормированное распределение Эрланга порядка 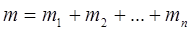с тем же самым параметром масштаба .

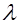5. При нормированное распределение Эрланга совпадает с показательным распределением.

Примечание. При увеличении порядка 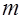математическое ожидание этого распределения остается неизменным, а его дисперсия стремится к нулю. Следовательно, случайная величина , имеющая нормированное распределение Эрланга, «становится все менее и менее случайной» и, в конце концов, вырождается в постоянную 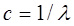. Это свойство нормированного распределения Эрланга очень удобно в практических приложениях. Оно позволяет, задаваясь различными значениями 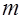, получать различную «степень случайности» случайной величины – от «сильной случайности», при до полного отсутствия случайности, при . 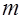При этом порядок нормированного распределения Эрланга можно рассматривать как своеобразную «меру случайности» случайной величины , используемой в качестве вероятностной модели какого-либо случайного параметра исследуемого объекта (например, времени прохождения сообщения через систему связи, времени безотказной работы технического устройства и т.п.).

Дата добавления: 2014-12-07