Введение. В данном разделе рассматриваются некоторые вопросы методики прогнозирования деятельности структур, сущность основных понятий в области прогнозирования

В данном разделе рассматриваются некоторые вопросы методики прогнозирования деятельности структур, сущность основных понятий в области прогнозирования, анализ методов прогнозирования.

После изучения данного раздела рекомендуется ответить на вопросы для самопроверки и на вопросы теста 3.

В случае если ответы на какие-либо вопросы вызовут затруднение или неуверенность, рекомендуется прочитать учебное пособие Голик, Е.С. Теория и методы статистического прогнозирования: учебное пособие /Е.С. Голик, О.В. Афанасьева. – СПб.: Изд-во СЗТУ, 2007. – 182 с. (с.79 – 94).

Часто на практике приходится иметь дело с задачей прогнозирования случайных величин, и это является предпосылкой применения вероятностных моделей. Вероятностные модели позволяют вычислить вероятность того, что будущее значение параметра прогнозируемого процесса будет меньше определенного числа, например, вероятность того, что

.

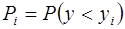Величина y может находиться в пределах , так как в соответствии с рис. 4.1 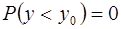и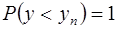

Рис. 1. Функция распределения вероятностей

Показанная на рисунке кривая распределения непрерывной случайной величины y является графиком функции распределения . Функция распределения существует как для непрерывных, так и для дискретных случайных величин и является универсальной характеристикой случайных величин.

Зная функцию распределения, можно найти вероятность попадания случайной величины на заданный участок :

.

Для непрерывных случайных величин очень часто рассматривается производная функции распределения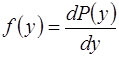

или плотность распределения непрерывной случайной величины y. Вероятность попадания случайной величины y на некоторый участок

.

Таким образом, прогнозирование вероятности того или иного события может быть осуществлено при прогнозировании рассмотренных функций распределения. Причем во многих практических случаях нет необходимости характеризовать случайную величину полностью, а бывает достаточно спрогнозировать только некоторые параметры распределения (например, математическое ожидание и дисперсию).

В некоторых случаях полученные в результате наблюдений за прогнозируемым процессом данные могут быть описаны широко известными распределениями непрерывных и дискретных случайных величин, среди которых: нормальное распределение, равномерное распределение, экспоненциальное распределение, распределение Пуассона и некоторые другие.

Если вид и параметры названных распределений не меняются по времени и в распоряжении имеется достаточное по объему количество наблюдений, то решение задачи прогнозирования не вызывает особых затруднений. Строится эмпирическое распределение, решается вопрос о выборе для данного эмпирического распределения теоретической кривой распределения и по ней с требуемой точностью производится прогнозирование. Однако на практике, как правило, в распоряжении исследователя имеется ограниченная информация о процессе, и, кроме того, не всегда можно гарантировать неизменность вида и параметров распределения. Эти условия предопределяют применение более сложных вероятностных моделей, базирующихся на последних достижениях теории вероятностей. К таким наиболее интенсивно разрабатываемым областям теории вероятностей относится, в частности. Теория малых выборок и теория суммирования случайного числа независимых случайных величин.

§ 1. Приложение теории суммирования случайного числа
независимых случайных величин в задачах прогнозирования

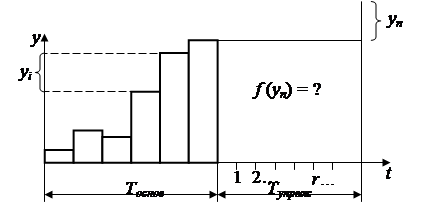
Постановка задачи. В результате анализа объекта прогнозирования и прогнозного фона на периоде ретроспекции (периоде основания прогноза) установлено, что процесс развития системы может быть представлен ступенчатым процессом (последовательностью скачков, совершаемых в случайные моменты времени). Величина скачка (рис. 2) является случайной величиной, поведение которой описывается законом распределения . Число скачков n на периоде упреждения прогноза является случайным, распределенным по закону . Требуется определить функцию распределения выходного параметра системы y.

Рис. 2. Постановка задачи

Решение. Традиционным (основным) аналитическим аппаратом теории вероятностей и математической статистики является аппарат характеристических функций. Известно, что если – действительная случайная величина, то существует комплексная случайная величина 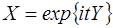(где – мнимая единица, t – действительное число).

Функция вида ,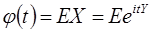

где E – символ математического ожидания, называется характеристической функцией случайной величины , то есть характеристическая функция случайной величины есть математическое ожидание комплексной случайной величины .

Характеристическая функция безразмерна, а параметр t имеет размерность, обратную размерности случайной величины .

Используем основные свойства характеристических функций для решения задачи, из условия решения которой известно, что выходной параметр системы y зависит как от случайного числа скачков n на периоде упреждения, так и от случайной величины каждого скачка. При этом случайные величины 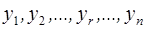независимы, одинаково распределены и не зависят от случайной величины n.

Примем, что число скачков на периоде упреждения прогноза может быть определено законом Пуассона

,

с параметром , причем для распределения Пуассона справедливо соотношение .

Случайная же величина y (величина скачка) имеет стандартное нормальное распределение 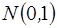с параметрами , и плотностью вероятности

.

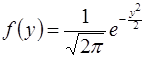Таким образом, чтобы получить закон распределения выходного параметра, необходимо рассмотреть распределение суммы пуассоновского числа стандартных нормальных величин.

На основании мультипликативного свойства характеристической функции – характеристическая функция суммы независимых случайных величин равна произведению характеристических функций случайных величин, то есть, если 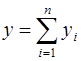, то

,

можно записать, что интегральная функция распределения суммы случайного числа n случайных величин определяется характеристической функцией

,

где – характеристическая функция случайной величины .

Рассмотрим характеристическую функцию стандартного нормального распределения

Так как интеграл 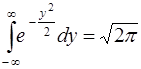, то .

Отсюда характеристическая функция суммы пуассоновского числа стандартных нормальных величин имеет вид

.

Для определенности случай 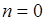из рассмотрения исключим.

Тогда

.

Исходя из формулы обращения

;

,

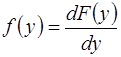тогда

.

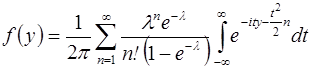В результате интегрирования получим искомую плотность распределения

.

В табл.6.1. приведем формулы для характеристических функций, наиболее часто встречающихся при решении практических задач.

Решим поставленную задачу при условии, что величина скачка равномерно распределена на интервале 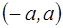. Такое допущение о законе распределения скачка представляется целесообразным для коротких динамических рядов. Симметричность интервала не снижает общности рассуждений.

Характеристическая функция для функции распределения суммы случайного числа случайных величин , распределенных равномерно на интервале ,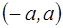

.

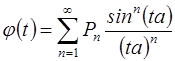Таблица 1. Характеристические функции

Распределение	Плотность распределения	Характеристическая функция
Равномерное	,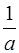
Равномерное	,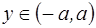
Показательное	,
Гамма	,
Нормальное	,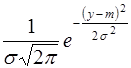

В соответствии с формулой обращения запишем формулу для плотности распределения .

Изменяя порядок суммирования и интегрирования и учитывая, что симметричные законы распределения в характеристической функции не имеют членов, содержащих мнимую единицу, плотность распределения

представим в виде

.

Используя табличный интеграл вида , находим плотность распределения выходной величины:

,

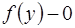при , где и , при , .

В табл. 2 приведены выражения для плотностей распределения выходной координаты при других условиях решениях поставленной задачи.

Таблица 2. Расчетные соотношения для плотности распределения величины Y

Закон распределения числа скачков n	Закон распределения величины скачка y	Плотность распределения
Пуассона, параметр	Нормальный, параметры
То же	Экспоненциальный, параметр
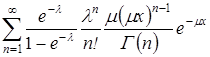
То же	Гамма-, параметры m, k
То же	Логнормальный, параметры
То же	Равномерный [–a, a]
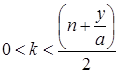
Биномиальный, параметр р	Нормальный, параметры
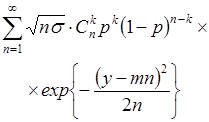
То же	Экспоненциальный, параметр
То же	Гамма-, параметры m, k

Необходимо помнить, что если и , а 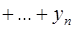, то для математического ожидания суммы случайного числа случайных слагаемых справедлива так называемая формула Вальда

.

Дисперсия суммы может быть определена через второй момент

,

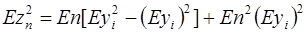откуда

.

Рассмотрим еще один подход, при котором теоретическая вероятностная модель сочетается с экстраполяционной моделью на ЭВМ. Этот подход применяется тогда, когда вероятностную модель трудно составить из-за больших неопределенностей или модель трудно исследовать из-за ее сложности. При использовании этого метода неопределенности «реализуются» случайным образом путем использования процедуры Монте-Карло.

Дата добавления: 2014-12-07