Ориентированный процесс случайного блуждания как метод вероятностного моделирования

В основу данного метода положен подход, не связанный с использованием жесткой структуры модели и серьезными требованиями к объему априорной информации. Сущность метода заключается в представлении используемого для прогнозирования динамического ряда в качестве определенным образом ориентированного процесса случайного блуждания.

Значение изменяющегося параметра объекта прогнозирования для каждого момента на периоде ретроспекции можно представить в виде

()

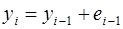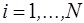где – значение динамического ряда в i -й момент времени (год) периода ретроспекции;

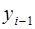– значение динамического ряда в предыдущий момент времени;

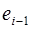– приращение переменной объекта прогнозирования в i -й момент времени по сравнению с предыдущими;

N – число значений динамического ряда.

Поскольку приращения носят случайный характер, для них можно определить вид закона распределения и его параметры. При этом нужно учесть характер зависимости последующих приращений от предыдущих.

Предполагается, что в период упреждения характер изменений динамического ряда сохраняется. Тогда, используя характеристики приращений, метод статистических испытаний можно применить для моделирования приращений в период упреждения прогноза.

Значение единичной реализации прогноза на каждом последующем шаге прогнозирования будет

, ()

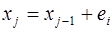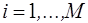где j – номер шага на периоде упреждения;

M – число шагов на периоде упреждения;

x_j-1 – значение переменной объекта прогнозирования на предыдущем шаге;

e_j – моделируемое значение приращение на j -м шаге.

Производя данную процедуру до момента упреждения, получаем значение точечного прогноза ,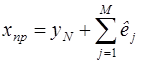

где – точечный прогноз на М -й период упреждения; 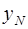– конечное значение динамического ряда.

При разыгрывании данной процедуры многократно образуется совокупность случайных значений точечного прогноза. По полученной выборке значений определяется среднее значение прогноза и его дисперсия:

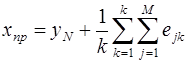; (1)

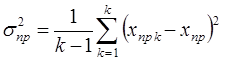, (2)

где k – число реализаций точечного прогноза;

e_jk – разыгрываемое значение приращения на j -м шаге периода упреждения в k -й реализации точечного прогноза;

– значение k -й реализации точечного прогноза, определяемое по зависимости (1).

Таким образом, процедура прогнозирования сводится к многократной имитации приращений на периоде упреждения и к последующему определению статистических характеристик (среднего и дисперсии) реализаций точечного прогноза.

При наличии репрезентативной выборки приращений моделирование можно осуществить в соответствии с определенным по этой выборке эмпирическим законом распределения приращений.

Для коротких динамических рядов можно применить допущение о нормальности отклонений значений динамического ряда от тренда. При этом допущении плотность распределения приращений также является нормальной.

При наличии на периоде ретроспекции малого объема (короткие динамические ряды) для моделирования приращений целесообразно использовать двумерное нормальное распределение. Двумерная плотность вероятности зависит от пяти параметров:

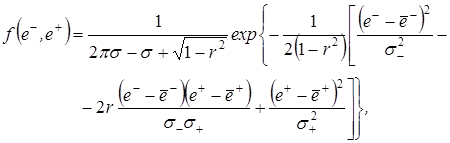
где 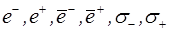– случайные значения, математические ожидания и среднеквадратические отклонения предыдущих и последующих приращений переменной прогнозирования, соответственно;

r – коэффициент корреляции последующих приращений на предыдущие.

Графически определение предыдущих и последующих приращений показано на рис. 3.

Рис. 3. Определение предыдущих и последующих приращений

Очевидно, что одно и то же приращение в зависимости от того, относительно какой точки оно рассматривается, может быть как предыдущим, так и последующим. Однако первое приращение является только предыдущим.

При обработке исходного динамического ряда определяются оценки математических ожиданий и дисперсий предыдущих и последующих приращений. Множество предыдущих приращений 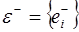определяется по зависимости

, .

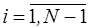Множество последующих приращений определяется по зависимости

,

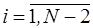
или .

По множеству 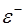определяются значения 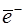и оценка дисперсии предыдущих приращений:

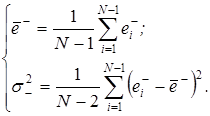
Соответственно по множеству 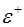определяются значения 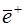и оценка дисперсии 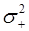последующих приращений:

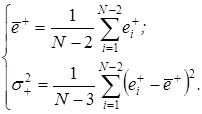
Оценка значения коэффициента корреляции 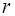определяется по зависимости

.

Для моделирования случайных приращений на периоде упреждения используется алгоритм моделирования двумерного распределения. Для рассматриваемого случая моделирующая зависимость последующих приращений 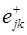имеет вид

При моделировании случайного значения 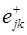на первом шаге в каждой k -й реализации 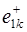предыдущее значение равно значению последнего приращения на периоде основания , то есть

.

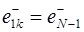При моделировании приращений на следующих шагах периода упреждения

.

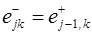Оценка коэффициента корреляции, определяемая по выборкам малых объемов, является случайной.

Плотность вероятности выборочного коэффициента корреляции имеет сложный вид. При принятом допущении о нормальности распределения приращений используется нормализующее преобразование Фишера.

Случайная величина z распределена нормально с параметрами

; ,

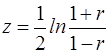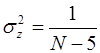где r – значение выборочного коэффициента корреляции.

Моделируем значение z как нормально распределенную случайную величину по зависимости ,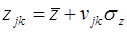

где 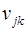– нормированная нормально распределенная случайная величина, моделируемая с помощью алгоритма.

Осуществляя обратный по отношению к преобразованию Фишера переход, получим случайное значение коэффициента корреляции

С учетом изложенного моделирование приращений на периоде упреждения включает выполнение следующих действий.

1. Обращение к датчику нормированных нормально распределенных случайных чисел и получение .

2. Вычисление случайного значения .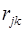

3. Обращение к датчику равномерно распределенных случайных величин и получение числа .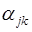

4. Вычисление приращения 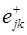при полученном значени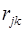и и .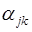

5. Многократная имитация приращения и вычисление характеристик прогноза.

Вопросы для самопроверки по разделу 3

1. Какие существую виды прогнозов?

2. Как строятся прогнозные модели?

3. Как осуществляется оценка параметров прогнозной модели?

4. По каким критериям происходят выбор оптимального вида прогнозной модели?

5. Как можно оценить вероятность попадания случайной величины в заданный участок?

6. Приведите пример теории суммирования случайного числа независимых случайных величин в задачах прогнозирования?

7. Какой подход применяется, когда вероятностную модель трудно составить из-за больших неопределенностей (или ее сложности)?

8. В каком случае динамический ряд целесообразно представить в виде ориентированного процесса случайного блуждания?

9. Является ли случайной оценка коэффициента корреляции, определяемая по выборке малых объемов?

Раздел 4. Структуризация вероятностных моделей неопределенности

Дата добавления: 2014-12-07