Оценка функций распределения и плотности

В случае, когда нет никакой информации о функции распределения некоторой случайной переменной, приходится оценивать полную функцию распределения из элементов пробы.

Пусть 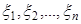представляет собой пробу из 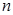элементов, а упорядоченная проба, полученная из данной пробы, обозначается символом . Функция

распределения, основанная на опыте , определяется следующим образом:

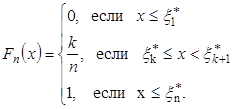. (42)

Поскольку функция является относительной частотой такого события, при котором результат эксперимента меньше, чем и функция 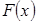(неизвестная функция распределения) является вероятностью такого же события, то по законам больших чисел функция будет близка к функции 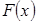с большой вероятностью при достаточно большом 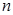. Это означает, что функцию можно считать некоторой оценкой функции .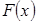

Гистограмма. Для оценки функции плотности применяется так называемая гистограмма. Гистограмма пробных элементов 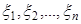может быть получена следующим образом. Предположим, что все полученные пробные элементы находятся между числам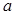и и 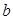, то есть

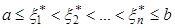. (43)

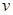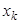Разделим интервал на одинаковых частей с точками разделения и рассчитаем относительную частоту такого события, при котором некоторый пробный элемент попадает между точками и . Если данную относительную частоту изобразить вертикально над интервалом 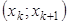, то получится гистограмма. Путем соответствующего выбора значения 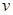(следует выбирать примерно ) может быть достигнуто состояние, при котором гистограмма будет близка к функции плотности с большой вероятностью.

Дата добавления: 2014-12-07