Исследование гипотез

Часто приходится отвечать на вопрос о правильности или неправильности некоторой гипотезы. Например, если на каком-то заводе приняли определенную партию товара, то не обязательно знать точно, сколько процентов составляют бракованные предметы в партии товара. Обычно достаточно определить, что относительное количество бракованного товара больше или меньше чем 3%. В первом случае партия товара будет отвергнута, а во втором – принята. Для реализации исследований статистических гипотез служат статистические пробы.

Проба 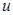. Пусть 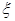представляет собой случайную переменную с нормальным распределением, с известной дисперсией 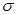. Надо проверить такую гипотезу, равняется ли математическое ожидание случайной величины 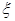определенному числу .

Для контроля данной гипотезы выбирается проба из 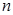элементов таким образом, что элементы пробы выбираются независимо друг от друга. Пусть результатом снятий проб будут величины 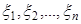. Проведем расчет величины

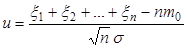. (30)

Можно увидеть, что случайная переменная 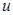имеет нормальное распределение, дисперсию 1; если выполняется гипотеза 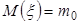, то 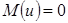. Таким образом, при выполнении данной гипотезы действительно следующее соотношение:

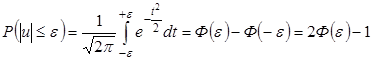. (31)

Пусть 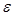будет таким, что можно было выполнить соотношение

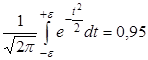. (32)

В таком случае, если из пробы получено такое значение 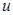, абсолютная величина которого больше чем 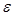, то гипотеза 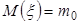может быть отвергнута, так как произошло событие, которое является невероятным при правильности гипотезы. Иными словами, если гипотеза 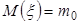отвергнута при выполнении условия 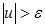, то только в 5% всех случаев будет отвергнута правильная гипотеза.

Бывает и так, что гипотеза 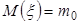не выполняется и все-таки принимается решение о правильности гипотезы. Вероятность ошибки такого рода нельзя определить так просто, как в случае проявления ошибки другого характера. Ибо в этом случае, если , все равно представляет собой малую величину. В таком случае более вероятно, что мы примем неправильную гипотезу 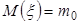, чем в том случае, когда имеет очень большое значение. В случае, если , гипотеза принимается с вероятностью

. (33)

Данная формула показывает, что если значение 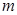близко к значению , то с вероятностью принимается гипотеза 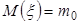; если значение 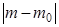велико, то гипотеза отвергается с вероятностью .

Функция называется силовой функцией пробы.

Проба . При использовании пробы 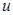незнание дисперсии обычно представляет собой серьезное затруднение. Пусть 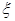означает случайную переменную с нормальным распределением. Проверяется гипотеза о том, равняется ли математическое ожидание случайной переменной 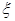определенному числу . Проведем 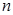экспериментов, результаты которых обозначим знаками 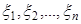. Оценивается значение выражения

, (34)

где

(35)

и

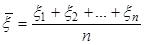. (26)

Функция распределения случайной переменной оценивается просто и ее значения могут быть собраны в таблицах. Имея таблицы, можно решить вопрос о правильности гипотезы 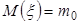, как это было показано при представлении пробы .

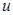При применении подобных проб можно решить вопрос о принятии или отклонении других статических гипотез. Ниже приведены только некоторые виды гипотез, для которых уже разработаны пробы.

Часто бывают такие случаи, когда необходимо знать закон распределения случайной переменной, а иногда закон распределения известен, но неизвестны его параметры. В таких случаях выдвигают гипотезу либо о законе распределения, либо гипотезу, связанную с параметрами закона распределения.

Наряду с выдвинутой гипотезой, рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. По этой причине эти гипотезы целесообразно различать.

Выдвинутую гипотезу называют нулевой (основной).

Конкурирующей (альтернативной) называют гипотезу, которая противоречит нулевой.

Различают гипотезы, которые содержат только одно и более одного предположений.

Простой называют гипотезу, содержащую только одно предположение.

Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.

Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Поскольку проверку производят статистическими методами, ее называют статистической. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, то есть могут быть допущены ошибки двух родов.

Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.

Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.

Для проверки нулевой гипотезы используют специально подобранную случайную величину, точное или приближенное распределение которой известно.

Статистическим критерием (или просто критерием) называют случайную величину, которая служит для проверки нулевой гипотезы.

Наблюдаемым значением называют значение критерия, вычисленное по выборкам.

После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другая – при которых она принимается.

Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.

Областью принятия гипотезы (область допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают.

Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы – гипотезу принимают.

Поскольку критерий – одномерная случайная величина, все ее возможные значения принадлежат некоторому интервалу. Поэтому критическая область и область принятия гипотезы также являются интервалами и, следовательно, существуют точки, которые их разделяют.

В приложениях 5-9 приведены значения критических точек распределения 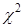, Стьюдента, Фишера-Снедекора, Кохрена.

Дата добавления: 2014-12-07