Аналитические методы решения уравнений в частных производных

МОТОРНЫЙ ВАГОН.

ПР1. в/в защита отопления.

ПР2. в/в защита прицепного вагона.

ПР3,ПР5. питание проводов фаз 81;83.

ПР19. вкл. ПРУ и питание провода 22.

ПР21. защита БВ-У.

ПР22. защита вспомогоательного компрессора.

ПР23. питание обмоток ДТЯ.

ПР28-ПР30. питание САУТ.

ПР31. питание БУКЗ.

ПР32. пренудительное резервирование.

ПР34,ПР35. мотор-вентилятор вогона.

ПР36,ПР38. освещение.

ПР39. отопление.

ПР40. дежурное освещение ПТРС.

ПР41-ПР43. резервирование.

Существует целый арсенал методов для решения уравнений в частных производных. Перечислим некоторые аналитические методы решения таких уравнений.

Метод разделения переменных. Уравнение с частными производными с n независимыми переменными сводится к n обыкновенным дифференциальным уравнениям. Решение краевых задач для уравнения Лапласа может быть найдено методом разделения переменных (методом Фурье) лишь для простейших областей (круг, прямоугольник, шар цилиндр и др.).

Метод интегральных преобразований Лапласа. Уравнение с частными производными в случае ограниченной пространственно одномерной области сводится к обыкновенному дифференциальному уравнению относительно изображений. Обратное преобразование производится согласно теореме Ващенко-Захарченко.

Метод функций Грина. Начальные и граничные условия заменяются системой простейших источников, и задача решается для каждого простейшего источника. Полное решение исходной задачи получается в результате суммирования решений для элементарных источников.

Вариационные методы. Вместо уравнения с частными производными решается задача минимизации функционала, соответствующего исходной задаче. Функция, доставляющая минимум этому выражению, является решением исходного уравнения.

2. Определение типа уравнения 2-го порядка и приведение его к каноническому виду.

Пусть 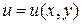- неизвестная функция двух независимых переменных 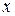и 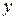. Тогда уравнением 2-го порядка называется уравнение вида

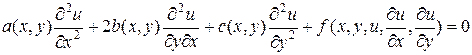(4)

Тип уравнения определяется в зависимости от величины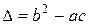

Если 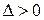, то уравнение гиперболического типа,

Если 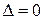, то уравнение параболического типа,

Если 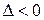, то уравнение эллиптического типа.

Для приведения (4) к каноническому виду следует написать уравнения характеристик

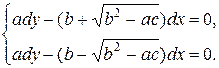(5)

и найти их общие решения.

Дата добавления: 2014-12-07