
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уравнения параболического типа при
|
|
|
|
Уравнения гиперболического типа при.
Обозначив общие интегралы системы уравнений (5) через 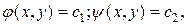 вводим новые независимые переменные
вводим новые независимые переменные  по формулам
по формулам  Тогда уравнение (4) примет вид
Тогда уравнение (4) примет вид  - канонический вид уравнения гиперболического типа.
- канонический вид уравнения гиперболического типа.
Общие интегралы системы уравнений (5) совпадают 
Вводим новые независимые переменные  по формулам
по формулам  где
где 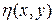 - функция, удовлетворяющая условию
- функция, удовлетворяющая условию  например,
например, 
Тогда уравнение (4) примет вид  - канонический вид уравнения параболического типа.
- канонический вид уравнения параболического типа.
Уравнения эллиптического типа при 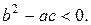
Общие интегралы системы уравнений (5) 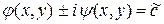 .
.
Вводим новые независимые переменные  по формулам
по формулам 
Тогда уравнение (4) примет вид  - канонический вид уравнения эллиптического типа.
- канонический вид уравнения эллиптического типа.
Пример 2. Определить тип уравнения и привести его к каноническому виду


 Уравнение эллиптического типа. Уравнение характеристик
Уравнение эллиптического типа. Уравнение характеристик
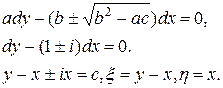

Подставляя полученные значения частотных производных в данное уравнение, получим


Ответ: 

3. Краевая задача для однородного волнового уравнения.
Дано однородное волновое уравнение  с начальными условиями
с начальными условиями  и краевыми условиями
и краевыми условиями 
Данная задача может быть решена методом Фурье, согласно которому решение записывается в виде  После подстановки
После подстановки  в данное уравнение, получим уравнения для функций
в данное уравнение, получим уравнения для функций  и
и  .
.
Решая уравнение  относительно функции
относительно функции  с граничными условиями
с граничными условиями  , получим
, получим
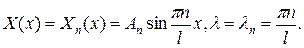
Решая уравнение 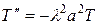 относительно функции
относительно функции  , получим
, получим
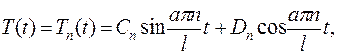
где  - некоторые константы. В силу однородности уравнения, мжно полагать, что
- некоторые константы. В силу однородности уравнения, мжно полагать, что  Следовательно, решение данного уравнения записывается в виде
Следовательно, решение данного уравнения записывается в виде


Для нахождения констант  воспользуемся начальными условиями
воспользуемся начальными условиями 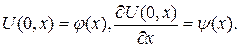
Тогда получим уравнения

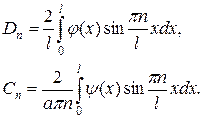
Пример Решить краевую задачу для однородного волнового уравнения

Решение записывается в виде
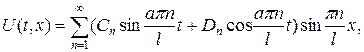
где  , т.к.
, т.к. 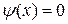 , а
, а  , т.к.
, т.к. 
 вычислим, воспользовавшись дважды интегрированием по частям
вычислим, воспользовавшись дважды интегрированием по частям

Ответ: 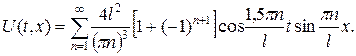
5. Краевая задача для однородного уравнения теплопроводности.
Дано уравнение 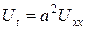 и условия
и условия 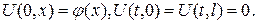 Согласно методу Фурье решение записывается в виде
Согласно методу Фурье решение записывается в виде  Подставляя его в данное уравнение, получим
Подставляя его в данное уравнение, получим
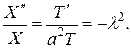
Для функции  имеем краевую задачу
имеем краевую задачу  , решение которой имеет вид
, решение которой имеет вид 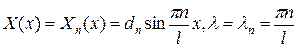 .
.
Для функции  имеем уравнение
имеем уравнение  решение которого имеет вид
решение которого имеет вид  Следовательно, решение уравнения теплопроводности имеет вид
Следовательно, решение уравнения теплопроводности имеет вид
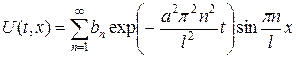
коэффициенты  находим из начального условия
находим из начального условия 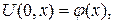 т.е.
т.е. 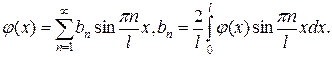
Пример 5. Решить краевую задачу для однородного уравнения теплопроводности

так как  то
то

Ответ: 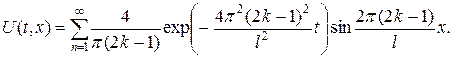
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 1083; Нарушение авторских прав?; Мы поможем в написании вашей работы!