Уравнения Лапласа

Численные методы решения

В курсовой работе требуется решить задачу Дирихле для уравнения Лапласа

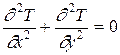(1)

одним из известных численных методов. Многие установившиеся процессы различной физической природы описываются этим уравнением.

Ставится задача о нахождении стационарного (не изменяющегося с течением времени) распределения температуры внутри многоугольника, если известно распределение температуры вдоль его сторон, т.е. необходимо решить задачу Дирихле для уравнения Лапласа.

Одна из главных трудностей, возникающих при решении этой задачи обусловлена сложной формой границы расчетной области. Аналитические решения удается получить лишь в частных случаях - для простейших областей (прямоугольник, круг, сектор, шар). Основными методами решения поставленной задачи являются численные методы.

Универсальным методом приближенного решения дифференциальных уравнений с частными производными является метод конечных разностей (или метод сеток). Суть его в следующем. Область непрерывного изменения аргументов (x,y) заменяется конечным (дискретным) множеством точек (узлов), называемым сеткой; вместо функций непрерывного аргумента рассматриваются функции дискретного аргумента, определенные в узлах сетки.

Будем считать, что заданная область покрыта прямоугольной сеткой. Узлы сетки, лежащие на границе области, называются граничными, а все остальные - внутренними. Прямоугольные сетки наиболее удобны при организации вычислительных алгоритмов (рис.1).

Уравнение (1) записывается для каждого внутреннего узла расчетной области, дифференциальное уравнение при этом заменяется системой алгебраических уравнений (разностными уравнениями).

Если полученная разностная краевая задача разрешима и ее решение при измельчении сетки приближается (сходится) к решению

исходной задачи для дифференциального уравнения, то оно и принимается за приближенное решение исходной задачи.

Рис.1. Прямоугольные сетки для решения задачи Дирихле

Производные, входящие в дифференциальное уравнение (1), заменяются соответствующими разностными отношениями:

;

.

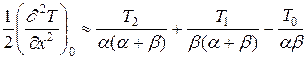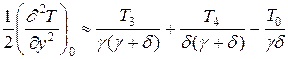Эти вычислительные шаблоны применяют там, где узлы прямоугольной сетки не являются равноотстоящими. Если a=b=h₁, а g=d=h₂, то применяют следующий вычислительный шаблон:

;
.

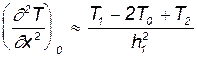В случае квадратной сетки уравнение (1) для нулевого узла будет иметь вид: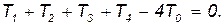

Так как вычислительные шаблоны связывают лишь несколько соседних узлов сетки, то матрица коэффициентов системы линейных уравнений для определения узловых неизвестных оказывается “разряженной”, т.е. содержит много нулевых элементов.

Рассмотрим пример использования приведенных вычислительных шаблонов для решения уравнения (1).

Пусть на сторонах трапеции (рис. 2), заданной координатами вершин A(0,2), B(2,2), C(4,0), D(0,0) известно распределение температуры T(x,y)=xy+x+y. Необходимо найти распределение температуры внутри области.

Рис. 2. Заданная расчетная область

Покроем квадратной сеткой рассматриваемую область (рис. 2) и составим систему линейных уравнений для определения неизвестных значений T₁ и T₂:

(2)

Вычислим значение температуры в граничных узлах (Т₃ – Т₉) сетки по заданной функции на границе T(x,y)=xy+x+y и подставим в систему уравнений (2). Получим систему для определения неизвестных значений T₁ и T₂:

Искомое решение T₁ =3, T₂ = 5. Выбор числа узлов сетки зависит от требуемой точности. Зная значения температуры в узлах, можно найти температуру в любой точке области, применяя интерполяционные формулы для функций нескольких переменных.

Если значения функции z=f (x,y) известны в вершинах прямоу-гольника a£ х£ b, c£ y£ d: z₁= f(a,c), z₂= f(b,c), z₃= f(b,d), z₄= f(a,d), то в любой точке (x,y) этого прямоугольника значения функции z=f(x,y) могут быть найдены по следующей формуле(h_x = b - a, h_y = d - c):

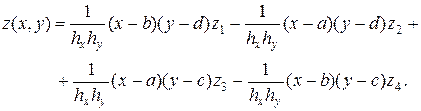
Для получения координат точек изотерм можно применить фор-мулы линейной интерполяции. Пусть в двух соседних узлах сетки

(x₁,y₁) и (x₂,y₂) известны значения температуры Т₁ и Т₂. Если необходимо найти координаты точки c заданной температурой T₀

min(Т₁,Т₂)£T₀£ max(Т₁,Т₂),

то можно воспользоваться формулами

, .

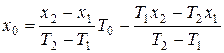Для рассматриваемой области (рис. 2) координаты изотермы T₀=2 будут равны: (0;2), (0,5;1), (1;0,5), (2;0).

Для решения поставленной задачи можно применить метод конечных элементов (МКЭ), который впервые был применен для численного решения дифференциальных уравнений в частных производных в середине 50-х годов ХХ столетия и с тех пор завоевал широкую популярность. Основная идея МКЭ состоит в том, что область расчета делится на конечное число элементов произвольной геометрической формы, и для каждого элемента рассматриваются так называемые базисные функции a_i, принимающие значения, равные 1 в i - м узле элемента и нулевые во всех других узлах.

Тогда значение искомой функции внутри элемента выражается через узловые неизвестные в виде

.

Наиболее распространенными конечными элементами для двумерных задач являются треугольные элементы (рис.1) с линейными базисными функциями (S - площадь треугольника):

,

,

.

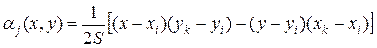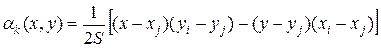Положительное значение площади S обеспечивается нумерацией вершин треугольника против часовой стрелки.

Рис. 3. Треугольный и прямоугольный конечные элементы

Пусть область расчета D c границей Г покрыта треугольными элементами. Вершины, расположенные внутри области, определяют узловые неизвестные. Для их определения составляют систему линейных уравнений:

, (3)

где u _j - значения искомой функции в узле j, а коэффициенты 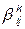определяются следующим интегралом:

. (4)

Внутреннее суммирование в системе уравнений (3) ведется по всем внутренним узлам, принадлежащим k-му элементу, а внешнее - по всем элементам, содержащим узел j. В рассматриваемой системе уравнений число узловых неизвестных равно числу уравнений. Для треугольных элементов

,

,

.

Невозможно дать общие рекомендации по триангуляции произвольной области. Существуют различные способы повышения точности при использовании МКЭ. Один из них - использование нелинейных конечных элементов и элементов специального вида для более точной аппроксимации границы области расчета и искомой функции.

Для прямоугольного конечного элемента (рис.3) могут быть построены нелинейные базисные функции

.

Коэффициенты системы МКЭ для прямоугольного элемента можно получить из интеграла (4).

МКЭ является одним из наиболее эффективных численных методов решения краевых задач, но, как и любой метод, он имеет свои недостатки. Так, точность полученных результатов зависит от триангуляции области. Количество выбранных треугольников, их вид и расположение могут влиять на точность получаемых решений. Особенно это относится к решению краевых задач в областях с угловыми точками.

Дата добавления: 2014-12-07