
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Розв’язання типового варіанта
|
|
|
|
Завдання 9.
Вступ до математичного аналізу
В задачах варіантів 1 – 25 знайти границі, не використовуючи правило Лопіталя.
1. а)  б)
б) 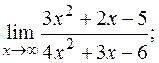 в)
в)  ;
;
г) 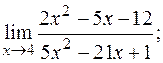 д)
д)  ; е)
; е) 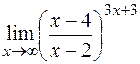 .
.
2. а) 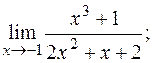 б)
б) 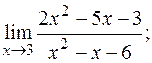 в)
в)  г)
г)  д)
д) 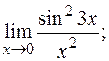 е)
е) 
3. a)  б)
б)  в)
в)  г)
г) 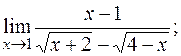 д)
д) 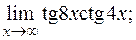 е)
е)  .
.
4. а) 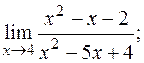 б)
б)  в)
в) 
г) 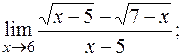 д)
д)  е)
е) 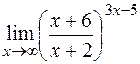 .
.
5. а) 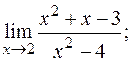 б)
б) 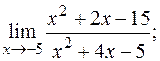 в)
в) 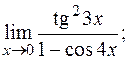 г)
г) 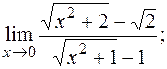 д)
д)  е)
е) 
6. a)  б)
б) 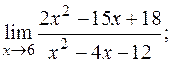 в)
в) 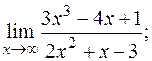 г)
г)  д)
д) 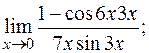 е)
е) 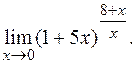
7. а)  б)
б) 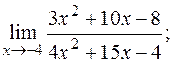 в)
в)  г)
г) 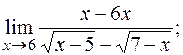 д)
д) 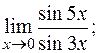 е)
е) 
8. а) 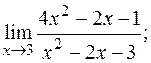 б)
б) 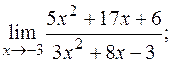 в)
в) 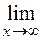
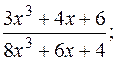
г) 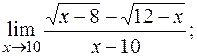 д)
д)  е)
е) 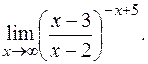
9. а) 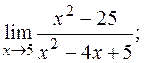 б)
б) 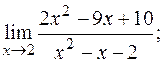 в)
в) 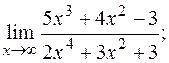
г)  д)
д)  е)
е) 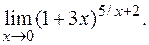
10. а)  б)
б) 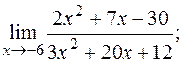 в)
в) 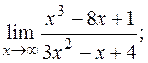 г)
г) 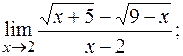 д)
д) 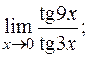 е)
е) 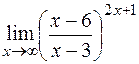 .
.
11. а) 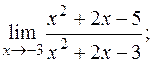 б)
б) 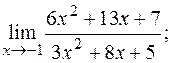 в)
в) 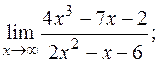 г)
г)  д)
д)  е)
е) 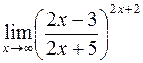 .
.
12. а)  б)
б) 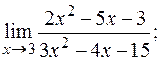 в)
в) 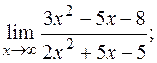 г)
г) 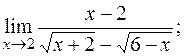 д)
д)  е)
е) 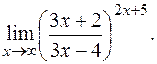
13. а) 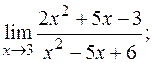 б)
б)  в)
в) 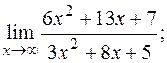 г)
г)  д)
д) 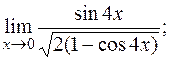 е)
е) 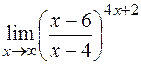 .
.
14. а) 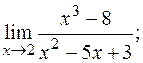 б)
б)  в)
в) 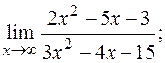 г)
г)  д)
д)  е)
е)  .
.
15. а)  б)
б) 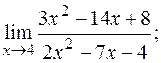 в)
в) 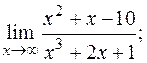 г)
г)  д)
д)  е)
е) 
16. а) 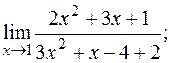 б)
б) 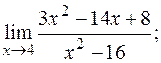 в)
в)  г)
г)  д)
д) 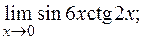 е)
е) 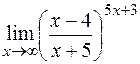 .
.
17. а) 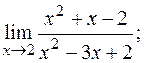 б)
б) 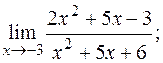 в)
в) 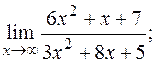 г)
г)  д)
д)  е)
е)  .
.
 18. а)
18. а) 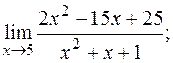 б)
б) 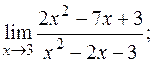 в)
в)  г)
г) 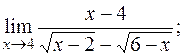 д)
д) 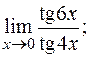
 е)
е) 
19. а) 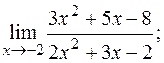 б)
б) 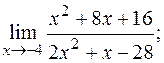 в)
в) 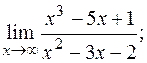 г)
г) 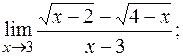 д)
д) 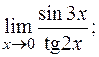 е)
е) 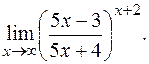
20. а) 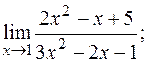 б)
б)  в)
в) 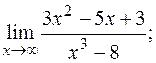 г)
г)  д)
д)  е)
е) 
21. а) 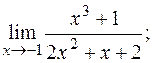 б)
б) 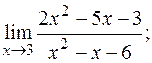 в)
в) 
г)  д)
д) 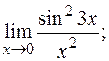 е)
е) 
22. а)  б)
б) 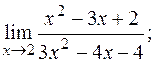 в)
в) 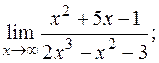 г)
г)  д)
д) 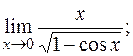 е)
е) 
23. а) 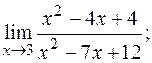 б)
б) 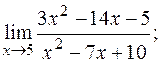 в)
в)  г)
г) 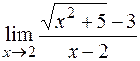 ; д)
; д)  е)
е) 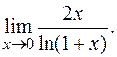
24. а) 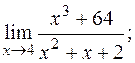 б)
б)  в)
в) 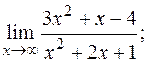
г) 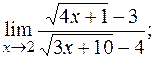 д)
д) 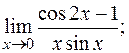 е)
е) 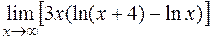 .
.
25. а) 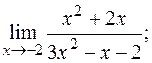 б)
б)  в)
в) 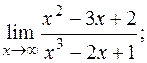 г)
г)  д)
д)  е)
е)  .
.
Завдання 10.
В задачах варіантів 1-25 дослідити задані функції на неперервність, знайти точки розриву і встановити характер точок розриву. Побудувати графіки.
1. а) 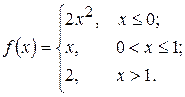 б)
б) 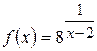 .
.
2. а) 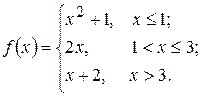 б)
б) 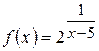 .
.
3. а)  б)
б)  .
.
4. а)  б)
б)  .
.
5. а)  б)
б)  .
.
6. а) 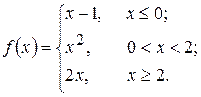 б)
б)  .
.
7. а) 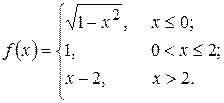 б)
б) 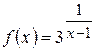 .
.
8. а)  б)
б)  .
.
9. а) 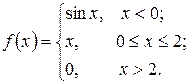 б)
б) 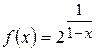 .
.
10. а) 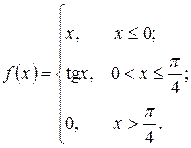 б)
б) 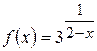 .
.
11. а) 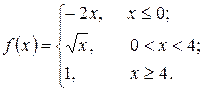 б)
б)  .
.
12. а) 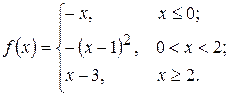 б)
б)  .
.
13. а)  б)
б)  .
.
14. а)  б)
б)  .
.
15. а)  б)
б) 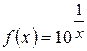 .
.
16. а) 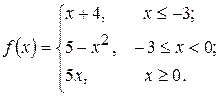 б)
б) 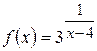 .
.
17. а)  б)
б) 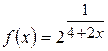 .
.
18. а) 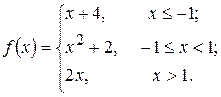 б)
б)  .
.
19. а) 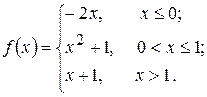 б)
б)  .
.
20. а)  б)
б) 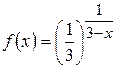 .
.
21. а) 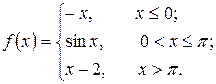 б)
б)  .
.
22. а)  б)
б)  .
.
23. а) 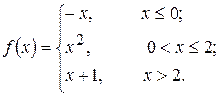 б)
б)  .
.
24. а)  б)
б) 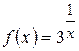 .
.
25. а) 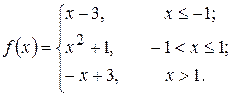 б)
б) 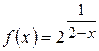 .
.
1. Знайти границі:
a)  ; b)
; b) 
в) 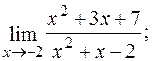 г)
г) 
д)  е)
е) 
► а) Під знаком границі маємо дробово-раціональну функцію, знаменник якої при х = 3 (граничне значення аргументу) відмінний від нуля. Користуючись теоремою про границю частки і замінюючи аргумент х його граничним значенням, маємо
 .
.
б) При х =1 знаменник дробу відмінний від нуля, чисельник дорівнює нулю. Отже, при 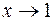 чисельник є величиною нескінченно малою, а знаменник – змінна величина, що має кінцеву границю. Оскільки частка від ділення нескінченно малої величини на змінну величину, що має кінцеву границю, є також нескінченно малою величиною, то границею даного дробу є нуль.
чисельник є величиною нескінченно малою, а знаменник – змінна величина, що має кінцеву границю. Оскільки частка від ділення нескінченно малої величини на змінну величину, що має кінцеву границю, є також нескінченно малою величиною, то границею даного дробу є нуль.
Отже,

в) При х = – 2 знаменник дробу дорівнює нулю, а чисельник від-мінний від нуля. Отже, при  знаменник є величина не скін-ченно мала, а чисельник – обмежена. Дана дріб є нескінченно вели-кою, умовно це позначається символом ¥. Таким чином,
знаменник є величина не скін-ченно мала, а чисельник – обмежена. Дана дріб є нескінченно вели-кою, умовно це позначається символом ¥. Таким чином,
 .
.
г) При х =2 чисельник і знаменник дробу дорівнюють нулю. Отже, безпосередня підстановка граничного значення аргументу призводить до невизначеного виразу виду  . Щоб розкрити невизначеність виду
. Щоб розкрити невизначеність виду  (відношення двох нескінченно малих величин), необхідно попередньо дріб спростити, розклавши на множники чисельник і знаменник та скоротивши дріб на (х – 2):
(відношення двох нескінченно малих величин), необхідно попередньо дріб спростити, розклавши на множники чисельник і знаменник та скоротивши дріб на (х – 2):
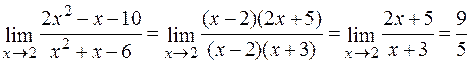 .
.
Слід відмітити, що аргумент х прямує до свого граничного значення 2, але не співпадає з ним. З цього приводу множник (х – 2) є відмінним від нуля при x ® 2.
д) При х ® ¥ маємо невизначений вираз виду 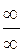 . Щоб знайти
. Щоб знайти
границю дробово-раціональної функції 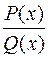 при
при  , необхідно попередньо чисельник і знаменник даного дробу поділити на
, необхідно попередньо чисельник і знаменник даного дробу поділити на 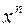 , де n – найвищий ступінь багаточленів Р (х) та Q (х). Поділивши чисельник і знаменник даного дробу на x 2, застосовуючи основні теореми про границі та властивості нескінченно малих, маємо
, де n – найвищий ступінь багаточленів Р (х) та Q (х). Поділивши чисельник і знаменник даного дробу на x 2, застосовуючи основні теореми про границі та властивості нескінченно малих, маємо
 .
.
е) Безпосередня підстановка граничного значення аргументу призводить до невизначеності виду  . Щоб розкрити цю невизна-ченість, помножимо чисельник та знаменник дробу на добуток
. Щоб розкрити цю невизна-ченість, помножимо чисельник та знаменник дробу на добуток 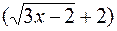 (
( ).
).
Потім скоротимо дріб на множник (х – 2), що є відмінним від нуля при  .
.
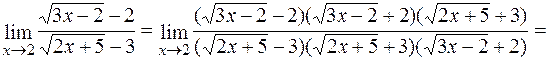

= 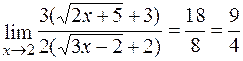 .◄
.◄
2.Знайти границі:
a)  б)
б) 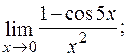 в)
в) 
►а) Першою визначною границею зветься границя відношення синуса нескінченно малої дуги до самої дуги. Відомо, що ця границя дорівнює одиниці, тобто 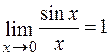 .
.
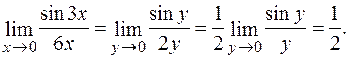 |
Нехай 3 х = у. Очевидно, що при
 і
і 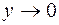 . Тоді
. Тоді
б) Відомо, що 1 – сos5 x = 2sin2 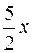 . Отже,
. Отже,
 .
.
в) Позначимо arctg2 x = y, тоді 2 x = tg y, очевидно, що при  і
і 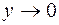 ; використовуючи теореми про границі, маємо:
; використовуючи теореми про границі, маємо:
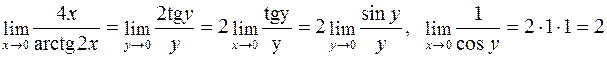 .◄
.◄
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 400; Нарушение авторских прав?; Мы поможем в написании вашей работы!