
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Розв’язання типового варіанта. 1. Задано трикутник з координатами вершин А(–2; 4); В(6; –2); С(8; 7)
|
|
|
|
1. Задано трикутник з координатами вершин А (–2; 4); В (6; –2); С (8; 7). Необхідно знайти: 1) довжину сторони АВ; 2) рівняння сторін АВ і АС та їх кутові коефіцієнти; 3) рівняння медіан, що проведені з вершин А і В, координати центру ваги трикутника; 4) величину кута А в радіанах з точністю до двох знаків; 5) рівняння висоти СТ, проведеної з вершини С на сторону АВ; 6) координати точки М, розташованої симетрично точці В відносно до прямої СТ; 7) Побудувати трикутник АВС медіани, висоту в системі координат 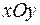 . Зробити малюнок.
. Зробити малюнок.
►1) Відстань між точками A (x 1, y 1) і B (x 2, y 2) площини визначається за формулою:
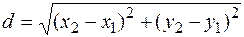 (11.1)
(11.1)
Застосовуючи (11.1), знаходимо довжину сторони АВ:
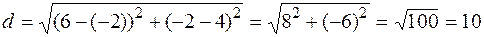 .
.
2) Рівняння прямої, що проходить через точки A (x 1, y 1) i B (x 2, y 2), має вигляд
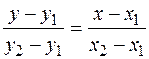 . (11.2)
. (11.2)
Щоб скласти рівняння сторони АВ, підставляємо в (11.2) координати точок А і В:

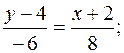
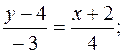 4 y – 16 = –3 x – 6;
4 y – 16 = –3 x – 6;
3 x + 4 y – 10= 0 (AB).
Для знаходження кутового коефіцієнта прямої АВ (КАВ), розв’я-жемо отримане рівняння відносно у:
4 y = –3 x + 10; y = 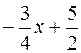 .
.
Отже,
K AB = 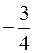 .
.
Підставляючи в (11.2) координати точок А і С, здобуваємо рівняння прямої АС:

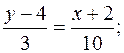
10 y – 40 = 3 x + 6; 3 x – 10 y + 46 = 0 (AC),
звідки кутовий коефіцієнт KAC = 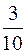 .
.
2. Нехай точка D – середина відрізку ВС, а точка Е – середина
відрізку АС.
Для визначення координат точок D і Е застосовуємо формули:
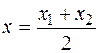 ; y =
; y = 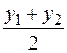 ;
;
xD = 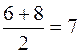 ; yD =
; yD = 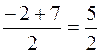 , D
, D 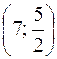 ,
,
xE = 
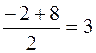 ; yE =
; yE =  , E
, E  .
.
Підставляючи координати точок А і D в (11.2), маємо рівняння медіани АD:
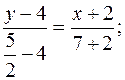
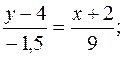
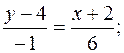
6 y – 24 = x – 2; x + 6 y – 22 = 0 (AD).
Аналогічно знаходимо рівняння медіани ВЕ:
5 x + 2 y – 26 = 0 (BE).
Центр ваги трикутника знаходиться в точці N перетину його медіан. Щоб знайти координати цієї точки, необхідно розв’язати систему рівнянь прямих АD і ВЕ.
Унаслідок розв’язку системи

маємо х = 4, у = 3.
Отже, N (4; 3) – точка перетину медіан.
Крім того, відомо, що точка перетину медіан ділить кожну медіану у відношенні 2:1 (починаючи з вершини), тобто
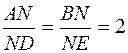 .
.
Тому координати точки N можна знайти також, застосовуючи формули ділення відрізку в даному відношенні:
x = 
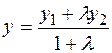 . (11.3)
. (11.3)
Підставляючи в (11.3) координати точок В і Е та вважаючи l = 2, маємо:

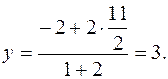
3) Гострий кут між прямими, кутові коефіцієнти яких, відпо-відно, дорівнюють К 1 та К 2, можна знайти за формулою
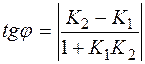 . (11.4)
. (11.4)
Шуканий кут А утворюється прямими АВ і АС, кутові коефі-цієнти яких знайдено раніше. Отже, застосовуючи формулу (11.4), маємо:
tg A = 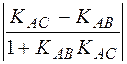 =
= 
Ð A = arctg 1,3548»53,480.
Скориставшись таблицями переведення градусної міри в радіанну, знаходимо
Ð A» 0,935 рад.
4) Рівняння прямої, що проходить через дану точку в даному напрямку, має вигляд
y – y 1= K (x – x 1). (11.5)
Для знаходження кутового коефіцієнта висоти СТ скористаємось умовою перпендикулярності прямих СТ і АВ: 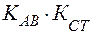 = –1. Оскільки
= –1. Оскільки 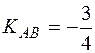 , то
, то 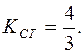
Підставляючи в (11.5) координати точки С, а також значення знайденого кутового коефіцієнта висоти СТ, маємо:
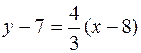 ; 3 y – 21 = 4 x – 32; 4 x –3 y – 11 = 0 (CT).
; 3 y – 21 = 4 x – 32; 4 x –3 y – 11 = 0 (CT).
5) Пряма АВ перпендикулярна до прямої СТ, а шукана точка М, симетрична точці В (2; –2) відносно до прямої СТ, належить прямій АВ. Крім того, точка Т є серединою відрізку МВ. Визначимо координати точки Т. Для цього розв’яжемо систему рівнянь, яку утворюють рівняння прямих АВ і СТ.
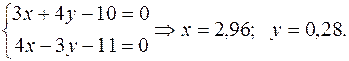
6) Враховуючи, що точка Т (2,96; 0,28) – середина відрізку МВ, а також користуючись формулами (11.3), знайдемо координати точки М:
2,96 =  ХM = -0,28;
ХM = -0,28;
0,28 = 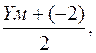 YM = 2,56.
YM = 2,56.
7) Трикутник АВС, медіани АD і ВЕ, точку N їх перетину, висоту СТ, що побудовані в системі координат 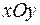 , подано на рис. 1.
, подано на рис. 1.


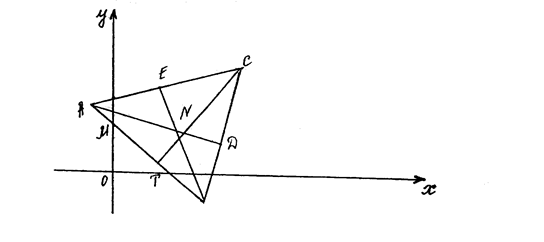
Рис. 1
2. Скласти канонічне рівняння гіперболи, що симетрична відносно до осей координат і проходить через точки А (8; 2 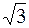 ) і В (–6;
) і В (–6; 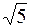 ). Знайти півосі, фокуси, ексцентриситети та рівняння асимптоти цієї гіперболи, а також усі точки перетину гіперболи з колом, центр якого знаходиться на початку координат, а радіус R = 6.
). Знайти півосі, фокуси, ексцентриситети та рівняння асимптоти цієї гіперболи, а також усі точки перетину гіперболи з колом, центр якого знаходиться на початку координат, а радіус R = 6.
► Канонічне рівняння шуканої гіперболи має вигляд
 . (11.6)
. (11.6)
За умови задачі точки А і В знаходяться на гіперболі, отже координати цих точок задовольняють рівнянню (11.6). Підставляючи в рівняння (11.6) замість поточних координат Х та У координати даних точок, одержуємо систему двох рівнянь відносно до параметрів a і b.
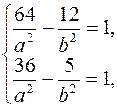 або
або 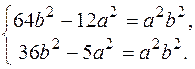
Віднімаючи від першого рівняння друге, маємо 28 b 2 – 7 a 2 = 0, звідси a 2 = 4 b 2. Після підставляння у перше рівняння маємо: 64 b 2 – 48 b 2 = 4 b 2 b 2, b 2 = 4, тоді a 2 = 16.
Шукане рівняння гіперболи має вигляд:
 (11.7)
(11.7)
Півосі гіперболи а =4; b =2. Визначаємо фокуси гіперболи F 1(– C; 0) i F 2(C; 0). Користуючись рівністю c 2 = a 2 + b 2, маємо:
c 2 =16+4=20, c =  .
.
Отже, F 1(2 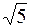 ,0) та F 2(–2
,0) та F 2(–2 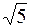 ,0) – фокуси гіперболи.
,0) – фокуси гіперболи.
Ексцентриситет гіперболи визначаємо за формулою 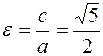 .
.
Рівняння асимптот гіперболи мають вигляд
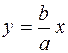 i
i 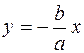 .
.
Отже, 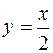 i
i 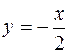 шукані рівняння асимптот. Рівняння кола, центр якого знаходиться на початку координат, має вигляд
шукані рівняння асимптот. Рівняння кола, центр якого знаходиться на початку координат, має вигляд
x 2 + y 2 = R 2.
Враховуючи, що R = 6, маємо
x 2 + y 2 = 36. (11.8)
Щоб знайти координати точок перетину гіперболи з колом, необхід-но розв’язати сумісно систему рівнянь (11.7) і (11.8).
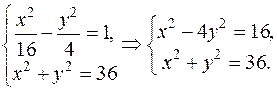
Отже, маємо: 5 y 2 = 20; y = ±2; x = ± 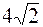 .
.
Точки перетину гіперболи з колом: M 1(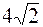 ;2); M 2(–
;2); M 2(– 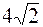 ;2); M 3(–
;2); M 3(– 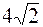 ;2); M 4 (
;2); M 4 (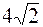 ;–2).
;–2).
Побудуємо в системі координат ХоУ гіперболу і коло (рис. 2)
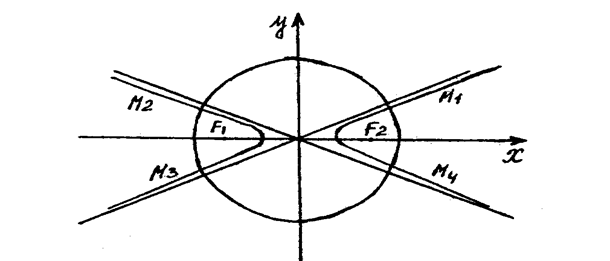


Рис. 2 ◄
3. Написати рівняння кривої, кожна точка якої знаходиться на однаковій відстані від точки F (4; 3) і прямої у =1. Отримане рівняння привести до простішого виду і побудувати криву.
► Нехай M (x, y) – довільна точка шуканої кривої. Опустимо з неї перпендикуляр до прямої y =1 (Рис.3). Очевидно, абсциса точки В дорівнює абсцисі точки М, а ордината точки В дорівнює 1, тобто B (x, 1). З умови задачі MF = MB. Таким чином, для кожної точки M (x, y) шуканої кривої справедлива рівність

або
(x – 4)2 + y 2 – 6 y + 9 = y 2 – 2 y + 1; (x -4)2=4 y -8.
Остаточно,
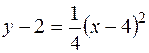 (11.9)
(11.9)
Геометричним образом отриманого рівняння є парабола з вершиною в точці O 1(4, 2). Рівняння параболи зведемо до простішого виду. Для цього нехай х – 4 = Х; у – 2 = У. Тоді рівняння (11.9) перетворюється до виду
Y = 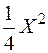 . (11.10)
. (11.10)
Перенесемо початок координат у точку О 1(4, 2), побудуємо нову систему координат ХО 1 У, вісі якої, відповідно, паралельні осям Ох і Оу.
Рівняння (11.10) є рівнянням параболи з вершиною в точці О 1 і віссю симетрії О 1 У (Рис. 3).
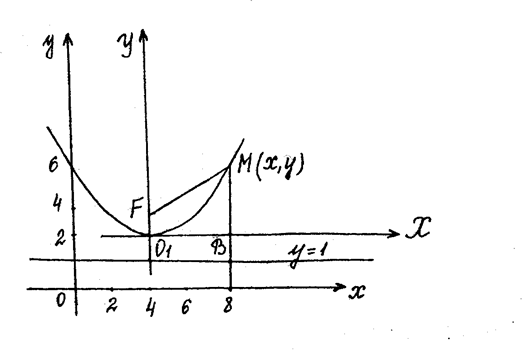
Рис.3 ◄
4. Дано координати точок: А (–1; 4; 2); В(0; 3; 3); С(4; –5; 3) і М(1; –3; 5).
Потрібно: 1) скласти рівняння площини Q, що проходить через точки А, В, С; 2) скласти канонічні рівняння прямої, що проходить через точку М перпендикулярно площині Q; 3) знайти точки перетину отриманої прямої з площиною Q та з координатними площинами х0у, х0z, y0z.
► 1) Рівняння площини, що проходить через 3 точки А (х 1; у 1; z 1), В (х 2; у 2; z 2) і С(х 3; у 3; z 3).
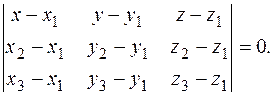 (11.11)
(11.11)
Підставляючи координати точок А, В, С в (11.11), маємо
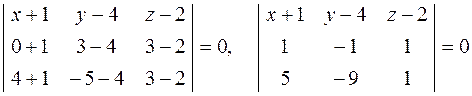 ,
,
або, розкладаючи визначник за елементами першого рядка, маємо
(x + 1)8 + (y – 4)4 + (z – 2)(–4) = 0,
2(x + 1) + y – 4 – z + 2 + 0;
2 x + y – z = 0 – рівняння площини Q.
2) Пряма в просторі задається канонічними рівняннями
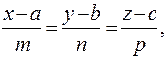 (11.12)
(11.12)
де а, в, с – координати точки, через яку проходить пряма, а m, n, p – координати напрямного вектора цієї прямої.
Умови перпендикулярності прямої (11.12) до площини Ax + By + + Cz + D = 0 мають вигляд:
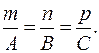
Запишемо умови перпендикулярності шуканої прямої до площи-ни Q:
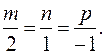
Цим умовам, зокрема, задовольняють наступні координати: m = 2; n = 1; p = –1.
Отже рівняння шуканої прямої:
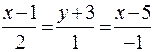 . (11.13).
. (11.13).
3) Запишемо рівняння прямої (11.13) у параметричному вигляді. Нехай
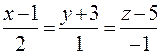 = t,
= t,
де t - деякий параметр. Тоді
х = 2 t + 1; y = t – 3; z = – t + 5. (11.14)
Підставивши (11.14) в рівняння площини Q, маємо
2(2 t + 1) + (t – 3) – (– t + 5) = 0; 6 t – 6 = 0; t = 1.
Покладаючи в (11.14) t = 1, знаходимо координати точки Р перетину прямої (11.13) з площиною Q. Отже, P (3; –2; 4).
Нехай Р1 – точка перетину прямої (11.13) з координатною площиною х0у.
Очевидно, що в цьому разі z = 0. Тоді, покладаючи в (11.14) z = 0, маємо t = 5; x = 11, y = 2. Отже, Р 1 (11, 2, 0) – точка перетину прямої (11.14) з площиною x0y.
Аналогічно знаходимо P 2(7; 0; 2) – точку перетину прямої (11.13) з площиною х0z; P 3 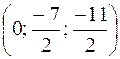 – точка перетину з площиною у0z.
– точка перетину з площиною у0z.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 1885; Нарушение авторских прав?; Мы поможем в написании вашей работы!