
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Аналітична геометрія
|
|
|
|
Завдання 4.
В задачах варіантів 1– 25 дани координати вершин трикутника АВС. Потрібно знайти: 1) рівняння сторін АВ і АС та їх кутові коефі-цієнти; 2) рівняння медіан, провдених з вершин А і В та точку їх перетинання; 3) кут А в радіанах з точністю до двох знаків; 4) рівняння висоти СТ, яка проведена з вершини С; 5) побудувати трикутник АВС, медіани, висоту в системі координат 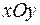 .
.
1. А (– 4, 2); В (4, – 4); С (6, 5).
2. А (–2, 1); В (6, –5); С (8, 4).
3. А (–3, –3); В (5, –9); С (7, 0).
4. А (2, 2); В (10, –4); С (12, 5).
5. А (4, –1); В (12, –7); С (14, 2).
6. А (–6, –2); В (2, –8); С (4, 1).
7, А (–8, –4); В (0, –10); С (2, –1).
8. А (–5, 5); В (3, –1); С (5, 8).
9. А (6, 2); В (14, –4); С (16, 5).
10. А (–4, –1); В (4, –7); С (6, 2).
11. А (–3, 0); В (5, –6); С (7, 3).
12. А (0, 5); В (8, –1); С (10, 8).
13. А (2, 6); В (10, 0); С (12, 9).
14. А (5, 3); В (13, –3); С (15, 6).
15. А (–10, 5); В (–2, –1); С (0, 8).
16. А (5, 5); В (13, –1); С (15, 8).
17. А (4, 6); В (12,0); С (14, 9).
18. А (1, 6); В (9, 0); С (11, 9).
19. А (–5, –1); В (3, –7); С (5, 2).
20. А (0, 1); В (8, –5); С (10, 4).
21. А (3, –1); В (11, –7); С (13, 2).
22. А (2, 6); В (10, 0); С (12, 9).
23. А (6, 7); В (14, 1); С (16, 10).
24. А (3, 0); В (11, –6); С (13, 3).
25. А (4, 4); В (12, –2); С (14, 7).
Завдання 5.
В задачах варіантів 1–25 дани координати точок А (х 1, у 1), В (х 2, у 2) та радіус кола R, центр якого знаходиться в початку координат. Необхідно: а) скласти канонічне рівняння еліпса з центром симетрії в точці О (0,0), який проходить через точки А і В; б) знайти півосі, фокуси та ексцентрисітет цього еліпса: в) знайти усі точки перетину еліпса та заданого кола; г) побудувати в системі координат хОу еліпс та коло.
| 1. А (8, -3), | В (4, 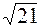 ), ),
| R = 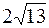 . .
|
2. А (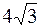 ,-4), ,-4),
| В (3,), | R = 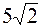 . .
|
3. А (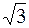 , 2), , 2),
| В (-1, 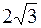 ), ),
| R = 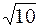 . .
|
4. А (1, - 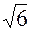 ), ),
| В (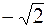 , 2), , 2),
| R = 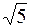 . .
|
5. А (-4, 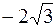 ), ),
| В (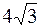 , 2), , 2),
| R = 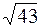 . .
|
6. А (3, 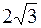 ), ),
| В (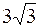 , -2), , -2),
| R = 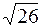 , ,
|
7. А (2, 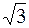 ), ),
| В (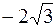 , 1), , 1),
| R = 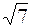 . .
|
8. А (4, 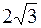 ), ),
| В (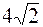 , , 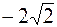 ), ),
| R = 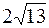 . .
|
9. А (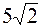 , , 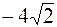 ), ),
| В (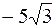 , 4), , 4),
| R = 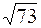 . .
|
10. А (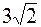 , , 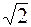 ), ),
| В (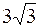 , -1), , -1),
| R = 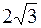 . .
|
11. А (2, 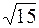 ), ),
| В (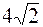 , ,  ), ),
| R = 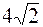 . .
|
12. А (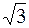 , , 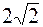 ), ),
| В (3, 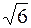 ), ),
| R = 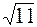 . .
|
13. 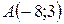 ;
; 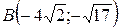 ;
; 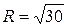 .
.
14. 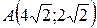 ;
; 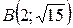 ;
; 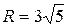 .
.
15. 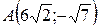 ;
; 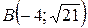 ;
;  .
.
16. 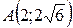 ;
; 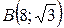 ;
; 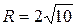 .
.
17. 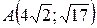 ;
; 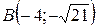 ;
; 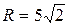 .
.
18. 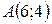 ;
; 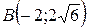 ;
; 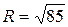 .
.
19. 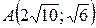 ;
; 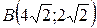 ;
; 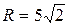 .
.
20. 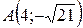 ;
; 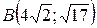 ;
; 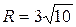 .
.
21. 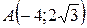 ;
; 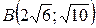 ;
; 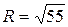 .
.
22. 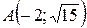 ;
; 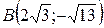 ;
; 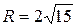 .
.
23. 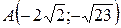 ;
; 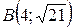 ;
; 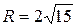 .
.
24. 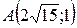 ;
; 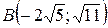 ;
; 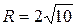 .
.
25. 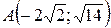 ;
; 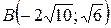 ;
; 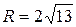 .
.
Завдання 6.
В задачах варіантів 1 – 25 дани координати точок А (х 1, у 1), В (х 2, у 2) та радіус кола R, центр якого знаходиться в точці О (0,0). Потрібно: а) скласти канонічне рівняння гіперболи з центром симетрії в точці О (0, 0), яка проходить через точки А і В, якщо фокуси гіперболи розташовані на осі абсцис; б) знайти півосі, фокуси, ексцентрисітет та рівняння асимптот цієї гіперболи; в) знайти усі точки перетину гіперболи та кола; г) побудувати в системі координат хОу гіперболу, її асімптоти та коло.
1. А (6, 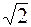 ); );
| В (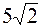 , 3); , 3);
| R = 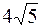 . .
|
2. А (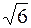 , –1); , –1);
| В (–4, 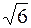 ); );
| R = 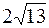 . .
|
| 3. А (10, 5); | В (–8, 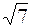 ); );
| R = 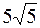 . .
|
4. А (16, 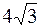 ); );
| В (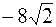 , –4); , –4);
| R =12. |
5. А (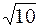 , -1) , -1)
| В (4, 2); | R = 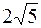 . .
|
6. А (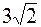 , -2) , -2)
| В (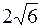 , , 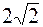 ); );
| R = 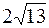 . .
|
7. А (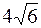 , -10); , -10);
| В (–8, 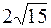 ); );
| R = 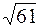 . .
|
8. А (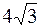 , -8); , -8);
| В (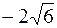 , 4); , 4);
| R = 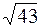 . .
|
9. А (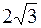 , -4); , -4);
| В (3, 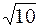 ); );
| R =10. |
10. А (–6, 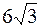 ); );
| В (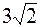 , 6); , 6);
| R = 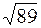 . .
|
11. А (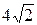 ,3); В (4
,3); В (4 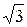 ,
, 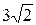 ); R =
); R = 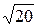 .
.
12. А (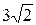 , 2); , 2);
| В (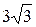 , ,  ); );
| R = 4. |
13. А (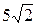 , 3); , 3);
| В (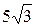 , , 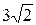 ); );
| R = 6. |
14. 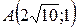 ;
; 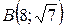 ;
; 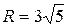 .
.
15. 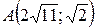 ;
; 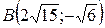 ;
; 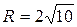 .
.
16. 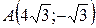 ;
; 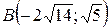 ;
; 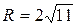 .
.
17. 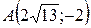 ;
; 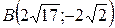 ;
; 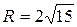 .
.
18. 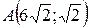 ;
; 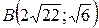 ;
; 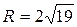 .
.
19. 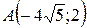 ;
; 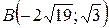 ;
; 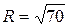 .
.
20. 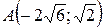 ;
; 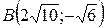 ;
; 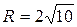 .
.
21. 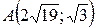 ;
; 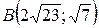 ;
; 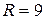 .
.
22. 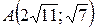 ;
; 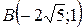 ;
; 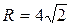 .
.
23. 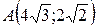 ;
; 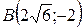 ;
; 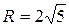 .
.
24. 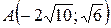 ;
; 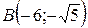 ;
; 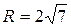 .
.
25. 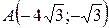 ;
; 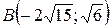 ;
; 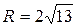 .
.
Завдання 7.
В задачах варіантів 1-25 задано координати точки 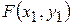 і рівняння прямої
і рівняння прямої 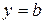 . Написати рівняння лінії, кожна точка якої знаходиться на однаковій відстані від точки
. Написати рівняння лінії, кожна точка якої знаходиться на однаковій відстані від точки 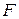 та від заданої прямої. Отримане рівняння привести до простішого вигляду.
та від заданої прямої. Отримане рівняння привести до простішого вигляду.
1. 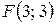 ;
;  . 2.
. 2. 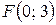 ;
; 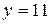 .
.
3. 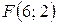 ;
; 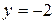 . 4.
. 4. 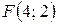 ;
; 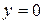 .
.
5. 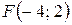 ;
; 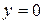 . 6.
. 6. 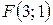 ;
; 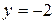 .
.
7. 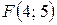 ;
; 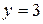 . 8.
. 8. 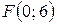 ;
; 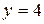 .
.
9. 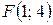 ;
; 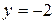 . 10.
. 10. 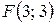 ;
; 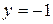 .
.
11. 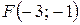 ;
;  . 12.
. 12. 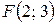 ;
;  .
.
13. 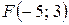 ;
;  . 14.
. 14. 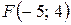 ;
; 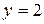 .
.
15. 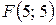 ;
; 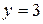 . 16.
. 16. 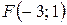 ;
; 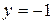 .
.
17. 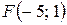 ;
; 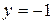 . 18.
. 18. 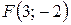 ;
; 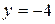 .
.
19. 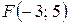 ;
; 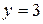 . 20.
. 20. 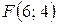 ;
; 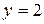 .
.
21. 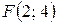 ;
; 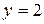 . 22.
. 22. 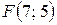 ;
; 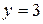 .
.
23. 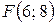 ;
; 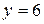 . 24.
. 24. 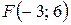 ;
; 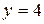 .
.
25. 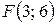 ;
; 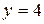 .
.
Завдання 8.
В задачах варіантів 1–25 дани координати точок А, В, С, М. Потрібно знайти: 1) рівняння площини Q, яка проходить через точки А, В, С; 2) канонічні рівняння прямої, яка проходить через точку М, перпендикулярно до площини Q; 3) координати точок перетину одержаної прямої з площиною Q та з координатними площинами 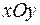 ,
,  ,
, 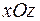 .
.
1. A (4, –7, 1); B (3, –5, 1); C (2, 0, 4); M (–2, –4, 4).
2. А (–5, 3, –7); В (1, 1, 3); С (–1, 4, 2); М (3, 3, 3).
3. А (2, –1, 3); В (–1, 2, 0); С (1, –4, –2); М (1, 2, –2).
4. А (–3, 4, –2); В (1, –3, –1); С (–1, –2, –4); М (3, 2, –4).
5. А (1, 2, 4); В (–5, 3, 7); С (4, –2, 6); М (–2, –3, –1).
6. А (–2, 1, –3); В (–4, 2, –6); С (3, –5, 1); М (6, 5, –7).
7. А (–1, 4, 2); В (3, –2, 4); С (5, –3, 7); М (–2, –5, 3).
8. А (–3, 1, 2); В (0, –1, 4); С (1, –3, 7); М (–1, –5, 7).
9. А (2, 5, 0); В (1, –3, 2); С (0, 2, 1); М (2, 3, 5).
10. А (1, 6, 4); В (2, 5, 5); С (6, –3, 5); М (3, –1, 7).
11. А (4, 1, 5); В (1, 4, 2); С (3, –2, 0); М (3, 4, 0).
12. А (–2, 5, –1); В (2, –2, 0); С (0, –1, –3); М (4, 3, –3).
13. А (2, 3, 5); В (–4, 4, –6); С (5, –1, 7); М (–1, –2, 0).
14. А (–4, 3, –7); В (2, 1, 3); С (0, 4, 2); М (4, 3, 3).
15. А (2, 3, 5); В (3, –1, 3); С (2, –4, –2); М (–3, –1, 3).
16. А (0, 2, –4); В (2, –2, –4); С (7, –1, 7); М (–1, 2, 6).
17. А (1, -4, 0); В (-1, 0, 1); С (2, 5, 5); М (5, 6, -5).
18. А (–1, 0, 2); В (2, 2, 3); С (–2, –3, –2); М (4, –1, 1).
19. А (1, –2, –2); В (–1, 2, –1); С (2, 7, 3); М (5, 8, –7).
20. А (4, 2, 0); В (6, –2, –1); С (–3, 3, –3); М (3, 3, –3).
21. А (–3, 3, –4); В (2, 10, 2); С (4, 2, –1); М (–3, 1, 7).
22. А (0, 3, –7); В (6, 1, 3); С (4, 4, 2); М (8, 3, 3).
23. А (4, 0, 1); В (3, 2, 1); С (2, 7, 4); М (–2, 3, 4).
24. А (1, 3, 1); В (7, –5, 5); С (–1, 5, –1); М (10, –2, 2).
25. А (2, 2, –4); В (4, –2, –4); С (9, –1, 7); М (1, 2, 6).
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 560; Нарушение авторских прав?; Мы поможем в написании вашей работы!