
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Розв’язання типового варіанта. 1. Нехай А(– 4; – І; 2); В(І; 0; 2); С(– І; 4; 6); D(– 2; – 3; 8) – точки координати вершин піраміди АВСD
|
|
|
|
1. Нехай А (– 4; – І; 2); В (І; 0; 2); С (– І; 4; 6); D (– 2; – 3; 8) – точки координати вершин піраміди АВСD. Необхідно: І) записати розкладання векторів 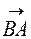 ,
, 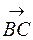 ,
, 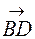 , за базисом
, за базисом 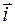 ,
, 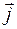 ,
, 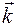 і знайти довжини цих векторів; 2) знайти кут між векторами
і знайти довжини цих векторів; 2) знайти кут між векторами 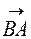 і
і 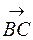 ; 3) знайти проекцію вектора
; 3) знайти проекцію вектора 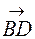 на вектор
на вектор 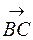 ; 4) знайти площу грані АВС; 5) Знайти об’єм піраміди АВСD.
; 4) знайти площу грані АВС; 5) Знайти об’єм піраміди АВСD.
►1) Відомо, що довільний вектор 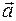 може бути розкладений за базисом
може бути розкладений за базисом 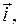
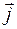 ,
, 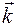 , таким чином:
, таким чином:
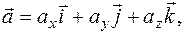
де ах, ау, аz – проекції вектора 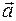 на координатні осі;
на координатні осі; 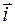 ,
, 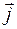 ,
, 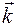 – одиничні вектори, напрямки яких збігаються з додатними напрямками осей OX, OY, OZ.
– одиничні вектори, напрямки яких збігаються з додатними напрямками осей OX, OY, OZ.
Нехай маємо точки M 1(x 1, y 1, z 1) i M 2(x 2, y 2, z 2), тоді проекції вектора 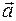 =
= 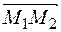 на координатні вісі дорівнють:
на координатні вісі дорівнють:
ax = x 2 – x 1; ay = y 2 – y 1; az = z 2 – z 1
і вектор 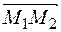 має вигляд
має вигляд
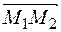 = (
= (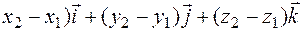 .
.
Отже, маємо
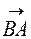 =
= 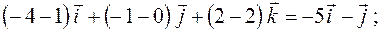
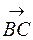 =
= 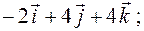
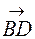 =
= 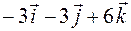 .
.
Довжину вектора 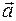 знаходимо за формулою
знаходимо за формулою
ç 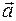 ç=
ç= 
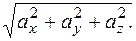
Маємо
ç 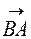 ç=
ç= 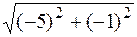 =
= 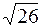 ,
,
ç 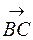 ç=
ç= 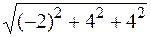 =6,
=6,
ç 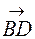 ç=
ç= 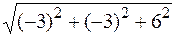 =
= 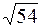 .
.
2) Косинус кута між векторами
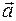 =
= 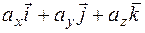 і
і 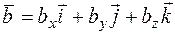
визначимо за формулою
cos 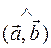 =
= 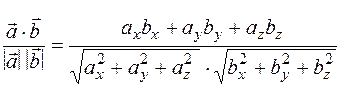 ,
,
де 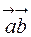 – скалярний добуток векторів
– скалярний добуток векторів 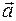 і
і 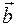 .
.
Отже,
cos 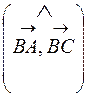 =
= 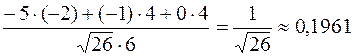 .
.
Таким чином, шуканий кут дорівнює
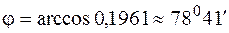 .
.
3) Проекція вектора 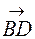 на вектор
на вектор 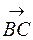 визначається за формулою:
визначається за формулою:
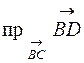 =
= 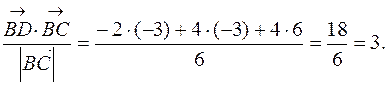
4) Площа грані АВС дорівнює половині площі паралелограма, побудованого на векторах 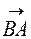 і
і 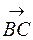 . Відомо, що модуль векторного добутку двох векторів дорівнює площі паралелограма, побудованого на цих векторах. Векторний добуток векторів
. Відомо, що модуль векторного добутку двох векторів дорівнює площі паралелограма, побудованого на цих векторах. Векторний добуток векторів 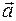 і
і 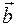 визначається за формулою:
визначається за формулою:
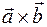 =
= 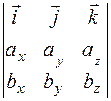 .
.
Позначимо векторний добуток 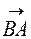 ×
× 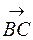 через вектор
через вектор 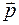 . Тоді площа грані АВС дорівнює половині модуля вектора
. Тоді площа грані АВС дорівнює половині модуля вектора 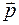 , тобто
, тобто
SABC= 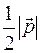 .
.
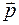 =
= 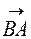 ×
× 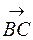 =
= 
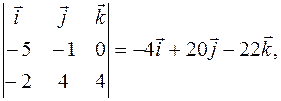 або
або 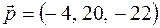
Отже,
SABC= 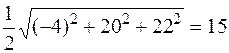 (кв.од.).
(кв.од.).
5) Об’єм паралелепіпеда, побудованого на трьох некомпланарних векторах 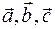 , дорівнює модулю їх мішаного добутку:
, дорівнює модулю їх мішаного добутку:
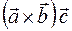 =
= 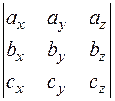 .
.
Отже, мішаний добуток векторів 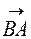 ,
, 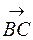 ,
, 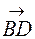 :
:
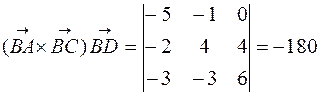 .
.
Шуканий об’єм V піраміди АВСD дорівнює одній шостій об’єму паралелепіпеда, тобто:
V= 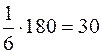 (куб.од.).◄
(куб.од.).◄
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 394; Нарушение авторских прав?; Мы поможем в написании вашей работы!