
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Розв’язання типового варіанта. В задачах варіантів 1-25 розв’язати задану систему лінійних алгебраїчних рівнянь трьома методами: 1) за формулами Крамера; 2) матричним методом; 3) методом
|
|
|
|
Завдання 2.
В задачах варіантів 1-25 розв’язати задану систему лінійних алгебраїчних рівнянь трьома методами: 1) за формулами Крамера; 2) матричним методом; 3) методом Жордана-Гаусса.
1.  3.
3. 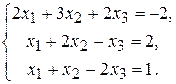 5.
5. 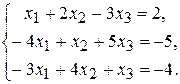 7.
7. 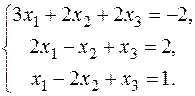 9.
9. 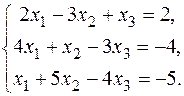 11.
11. 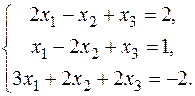
| 2. 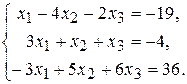 4.
4. 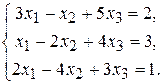 6.
6. 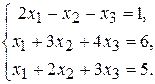 8.
8. 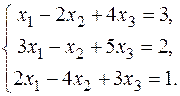 10.
10. 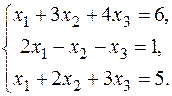 12.
12. 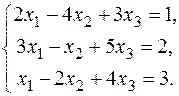 
| |
13. 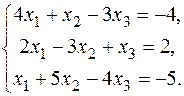 15.
15. 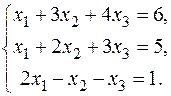 17.
17. 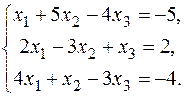 19.
19. 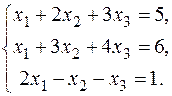 21.
21. 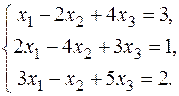 23.
23. 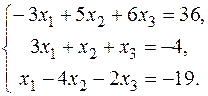 25.
25. 
| 14. 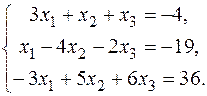 16.
16. 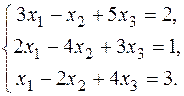 18.
18. 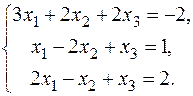 20.
20. 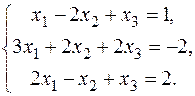 22.
22. 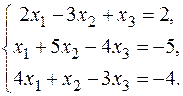 24.
24. 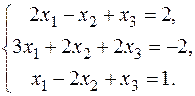
| |
1. Обчислити визначник четвертого порядку
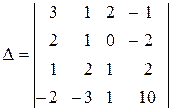 .
.
► Використаємо метод зниження порядку, який основано на застосуванні правила обчислення визначників за допомогою розкладання за елементами деякого рядка (стовпця). Використовуючи при цьому властивість визначників про лінійну комбінацію елементів рядків (стовпців), обертаємо в нулі усі, крім одного, елементи деякого рядка (стовпця).
В нашому випадку помножимо послідовно третій рядок на 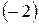 та
та 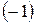 і додамо відповідно до першого та четвертого рядків. Отриманий визначник розкладемо за елементами третього стовпця.
і додамо відповідно до першого та четвертого рядків. Отриманий визначник розкладемо за елементами третього стовпця.
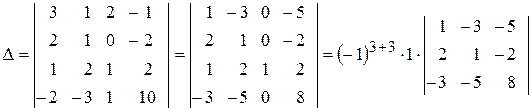 .
.
Далі обертаємо в нулі елементи першого стовпця, окрім елементу 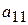 , помножаючи елементи першого рядка послідовно на
, помножаючи елементи першого рядка послідовно на 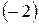 , 3 і додаючи відповідно до другого і третього рядків.
, 3 і додаючи відповідно до другого і третього рядків.
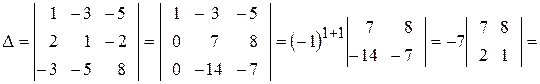
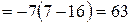 . ◄
. ◄
2. Розв’язати систему лінійних рівнянь двома способами: за правилом Крамера та за допомогою матриці, оберненої до матриці системи
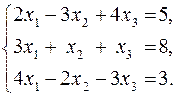
► 1) Формули Крамера мають вигляд:
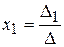 ,
, 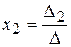 ,
, 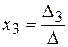 ,
,
де 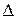 - визначник системи,
- визначник системи, 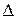 ¹ 0;
¹ 0; 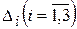 одержується із визначника системи
одержується із визначника системи 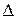 шляхом заміни і -го стовпця стовпцем, складеним з вільних членів системи рівнянь. Маємо
шляхом заміни і -го стовпця стовпцем, складеним з вільних членів системи рівнянь. Маємо
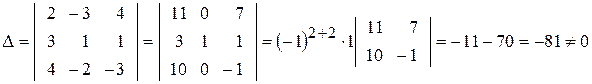 .
.
Отже, система має єдиний розв’язок.
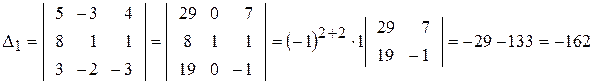 ,
,
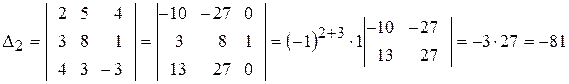 ,
,
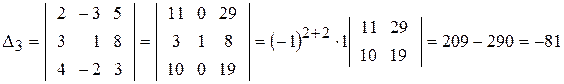 .
.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 442; Нарушение авторских прав?; Мы поможем в написании вашей работы!