
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Введение 2 страница
|
|
|
|
ЛАБОРАТОРНАЯ РАБОТА № 4 Свободные колебания систем с конечным числом степеней свободы. (2 часа)
Цель работы: расчет механических систем с конечным числом степеней свободы на собственные колебания.
Задачи работы: приобретение практических навыков расчета механических систем с конечным числом степеней свободы на собственные колебания.
Обеспечивающие средства: методика расчета механических систем с конечным числом степеней свободы на собственные колебания.
Задание: Составление систем уравнений движения. Уравнения Лагранжа второго рода, прямой и обратный способ.
Требования к содержанию отчета: по результатам работы оформляется отчет в соответствии с порядком выполнения работы.
Порядок выполнения.
Наиболее общий вид дифференциальных уравнений движения может быть получен в форме уравнений Лагранжа
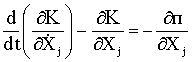 (4.1)
(4.1)
где K и П - кинетическая и потенциальная энергии соответственно; Xj и 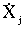 - обобщённые координаты и обобщённые скорости; j = 1, 2,…, n - число степеней свободы системы.
- обобщённые координаты и обобщённые скорости; j = 1, 2,…, n - число степеней свободы системы.
Известно, что при малых колебаниях около положения равновесия кинетическая и потенциальная энергии выражаются через обобщённые координаты и обобщённые скорости следующим образом:
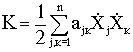 ;
; 
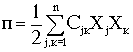 , (4.2)
, (4.2)
где ajk = akj - инерционные коэффициенты; Cjk = Ckj - квазиупругие коэффициенты, называемые также обобщёнными коэффициентами жёсткости.
Подставляя (4.2) в (4.1), получим систему однородных линейных дифференциальных уравнений с постоянными коэффициентами:
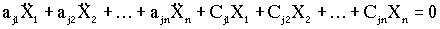 , , 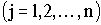 (4.3)
(4.3)
|
Однако составление уравнений движения по схеме Лагранжа не является обязательным, потому что во многих случаях прямой или обратный способы оказываются более удобными.
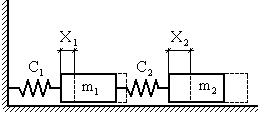
Рассмотрим особенности названных способов на примере системы с двумя степенями свободы, состоящей из тел с массами m1 и m2, соединённых пружинами с жесткостями C1 и C2 (рис.4.1,а).
За обобщённые координаты примем горизонтальные перемещения X1 и X2 грузов, отсчитываемые от положения равновесия, в которых отсутствуют деформации пружин. Удлинения пружин в процессе движения: 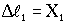 ;
; 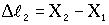 .
.
1.Основной способ (уравнения Лагранжа)
Кинетическая энергия рассматриваемой системы:
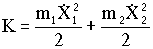 .
.
Потенциальная энергия деформации пружин:
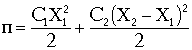 .
.
Вычислим производные, необходимые для подстановки в уравнения Лагранжа:
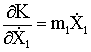 ;
; 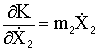 ;
;
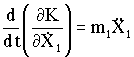 ;
; 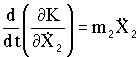 ;
;
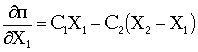 ;
; 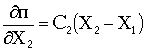 .
.
Подставляя вычисленные значения в (4.1), получим дифференциальные уравнения движения рассматриваемой системы
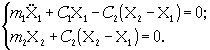 (4.3)
(4.3)
2.Прямой способ
Выделяем массы m1 и m2 и рассматриваем их как свободные тела под действием сил упругости, определяемых удлинениями l1 и l2 обеих пружин (рис. 4.1,б):
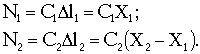
Дифференциальные уравнения движения грузов имеют вид
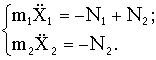
Подставляя значения N1 и N2, получим
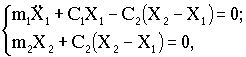
т.е. эти уравнения совпали с уравнениями (4.3).
 а
а
|
б 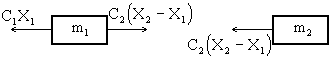
|
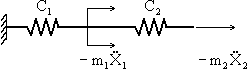 в
в
| |
| Рис. 4.1 |
3. Обратный способ
Отделяем грузы и рассматриваем упругий безмассовый скелет системы под действием кинетических реакций - сил инерции 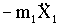 и
и 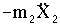 (рис. 4.1,в). В этой схеме первая пружина нагружена силой
(рис. 4.1,в). В этой схеме первая пружина нагружена силой 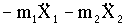 , а вторая - силой
, а вторая - силой 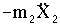 . Перемещение X1 конца первой пружины, равное её удлинению, можно записать в виде
. Перемещение X1 конца первой пружины, равное её удлинению, можно записать в виде
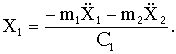
Перемещение правого конца второй пружины X2 равно сумме удлинений обеих пружин:
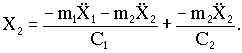
Из этих соотношений получим
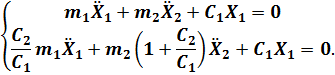
Таким образом, совпали формы записей дифференциальных уравнений движения по основному (уравнения Лагранжа) и прямому способам, а уравнения, полученные обратным способом, отличаются от них по форме. Это связано с тем, что при нашем выборе обобщённых координат кинетическая энергия имеет каноническую форму:
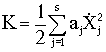 ,
,
т.е. не содержит произведений скоростей 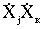 при
при 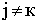 . При этом каждое из уравнений Лагранжа содержит только по одному обобщённому ускорению, как и при использовании прямого способа. Если обобщённые координаты выбрать так, чтобы потенциальная энергия имела каноническую форму
. При этом каждое из уравнений Лагранжа содержит только по одному обобщённому ускорению, как и при использовании прямого способа. Если обобщённые координаты выбрать так, чтобы потенциальная энергия имела каноническую форму
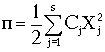 ,
,
то уравнения Лагранжа совпали бы с уравнениями, полученными обратным способом.
Сопоставляя полученные варианты записей по прямому и обратному способам, можно сделать следующее общее заключение: при составлении системы уравнений по прямому способу aij = 0 при i j, а при составлении по обратному способу Cij = 0 при i j.
Таким образом, пользуясь прямым способом, приходим в общем случае к системе:
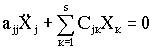 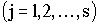 , (4.4) , (4.4)
|
а применяя обратный способ - к системе:
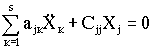 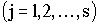 (4.5) (4.5)
|
Принципиально важно, что специальным выбором обобщённых координат можно одновременно придать каноническую форму как кинетической, так и потенциальной энергии. Такие координаты i (i = 1, 2,…, s) называются нормальными, или главными. При этом
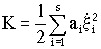 ,
, 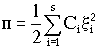
и уравнения Лагранжа принимают вид
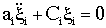 , , 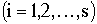 (4.6) (4.6)
|
Каждое из уравнений (4.6) интегрируется независимо от других. Иначе говоря, при использовании нормальных координат система представляет собой как бы совокупность независимых парциальных систем с одной степенью свободы.
Пример Пружина несёт две массы m = 2 кг каждая - одна на конце пружины, другая посередине (рис. 4.2,а). Средний диаметр пружины D = 4 см; диаметр проволоки пружины d = 0,6 см; число витков на каждой половине пружины n = 10. Определить частоты собственных колебаний системы.
а б
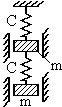
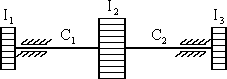
Рис. 4.2
Решение
Уравнения движения системы
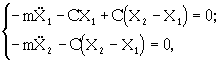
где X1 и X2 - смещения верхней и нижней масс соответственно; С - жёсткость пружины.
Решение системы уравнений ищем в виде
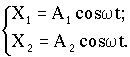
После подстановки получим систему однородных алгебраических уравнений
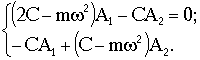
Частотное уравнение
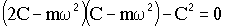 ,
,
или
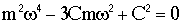 .
.
Корни частотного уравнения:
 ;
; 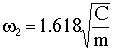 .
.
Жёсткость пружины:
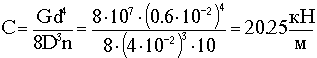 .
.
Собственные частоты: 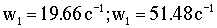 .
.
Исходные данные.
Определить частоты собственных колебаний системы в соответствии с рисунком 4.2 а.
| № варианта | Количество витков каждой половины пружины | Диаметр пружины, м | Диаметр проволоки пружины, м | Масса каждого груза, кг |
| 0,05 | 0,01 | |||
| 0,06 | 0,012 | |||
| 0,07 | 0,014 | |||
| 0,08 | 0,016 | |||
| 0,09 | 0,018 | |||
| 0,1 | 0,02 | |||
| 0,11 | 0,022 | |||
| 0,12 | 0,024 | |||
| 0,13 | 0,026 | |||
| 0,14 | 0,028 | |||
| 0,15 | 0,03 | |||
| 0,16 | 0,032 | |||
| 0,17 | 0,034 | |||
| 0,18 | 0,036 | |||
| 0,19 | 0,038 | |||
| 0,2 | 0,04 | |||
| 0,21 | 0,042 | |||
| 0,22 | 0,044 | |||
| 0,23 | 0,046 | |||
| 0,24 | 0,048 |
Контрольные вопросы
1 Способы составления уравнений движения механических систем.
2 Кинетическакя энергия системы.
3 Потенциальная энергия системы.
4 Уравнения Лагранжа второго рода.
5 Составление уравнений движения прямым способом.
6 Составление уравнений движения обратным способом.
7 Гармоническое колебательное движение. Параметры этого движения - амплитуда, фаза, период.
8 Циклическая частота и частота колебательного движения.
9 Количество частот собственных колебаний системы в зависимости от числа степеней свободы.
ЛАБОРАТОРНАЯ РАБОТА №5. Численное решение уравнений движения механической системы с несколькими степенями свободы. Применение метода Рунге Кутты реализованного в математических программах. (2 часа)
Цель работы: численное решение линейных дифференциальных уравнений с применением программы Mathcad.
Задачи работы: численное решение линейных дифференциальных уравнений с применением программы Mathcad.
Обеспечивающие средства: методика применения программы Mathcad для решения дифференциальных уравнений и их систем.
Задание: решение дифференциальных уравнений и их систем.
Требования к содержанию отчета: по результатам работы оформляется отчет в соответствии с порядком выполнения работы.
Порядок выполнения.
1. Общие положения.
Все математические операции в Маткаде можно осуществлять, используя встроенные функции и встроенные операторы.
Встроенные функции вызываются с помощью мастера функций – кнопки с изображением f (x), расположенной на инструментальной панели. При этом появляется окно с перечнем всех функций Маткада, из которого можно выбрать необходимую в данный момент функцию.
Встроенные операторы расположены на панели вычислений, которая вызывается кнопкой с изображением производной и интеграла на математической панели.
Во втором модуле «Работа со встроенными функциями Маткада» решаются с использованием встроенных функций различные математические задачи без привязки к конкретным прикладным задачам.
Модуль состоит из шести лабораторных работ. В первых четырех лабораторных работах приводится решение основных типов дифференциальных уравнений в Маткаде. Рассматривается несколько методов решения задачи Коши, решается краевая задача. Рассматривается решение разностных уравнений.
Две последние лабораторные работы посвящены построению различных регрессий, доверительных интервалов и проверке статистических гипотез.
В Маткаде имеется тринадцать встроенных функций для решения обыкновенных дифференциальных уравнений различными методами. Большинство из них требуют предварительного представления дифференциального уравнения в виде системы дифференциальных уравнений первого порядка.
Среди встроенных функций Маткада для решения дифференциальных уравнений есть функция их решения методом Рунге – Кутты с постоянным фиксированным шагом. Она имеет вид: rkfixed(v,x0,x k,n,F). Здесь v начальные условия, записанные в виде вектора, x0,xk – начальное и конечное значения аргумента, n- число шагов, F- правые части системы, записанные в виде вектора.
Возможно решение тем же методом с автоматическим выбором шага. Для этого служит функция rkadapt(y, x1, x2, n points, D). Эти методы требуют преобразования дифференциального уравнения в систему уравнений первого порядка.
В последних версиях Маткада появилась функция odesolve(х, b) (ordinary differential equation solution – решение обыкновенного дифференциального уравнения), позволяющая решать уравнение без его преобразования.
Здесь в скобках х – переменная интегрирования, b - верхняя граница изменения аргумента. Нижняя граница равна нулю.
2.Решение дифференциальных уравнений с помощью функции odesolve.
Задача 1. Используя встроенную функцию odesolve решить в Маткаде следующее нелинейное обыкновенное дифференциальное уравнение второго порядка с нулевыми начальными условиями:
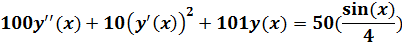
На рис. 1. показано это решение.
Итак, для решения с использованием этой функции нужно:
1. Ввести директиву given
2. Набрать дифференциальное уравнение. Знак производной набирается клавишей Ё английской клавиатуры, знак «=» - с логической панели,
3. набрать начальные условия,
4. набрать функцию odesolve,
| 5. | сформировать график, | ||||||
| 6. | Нажать клавишу F9. | ||||||
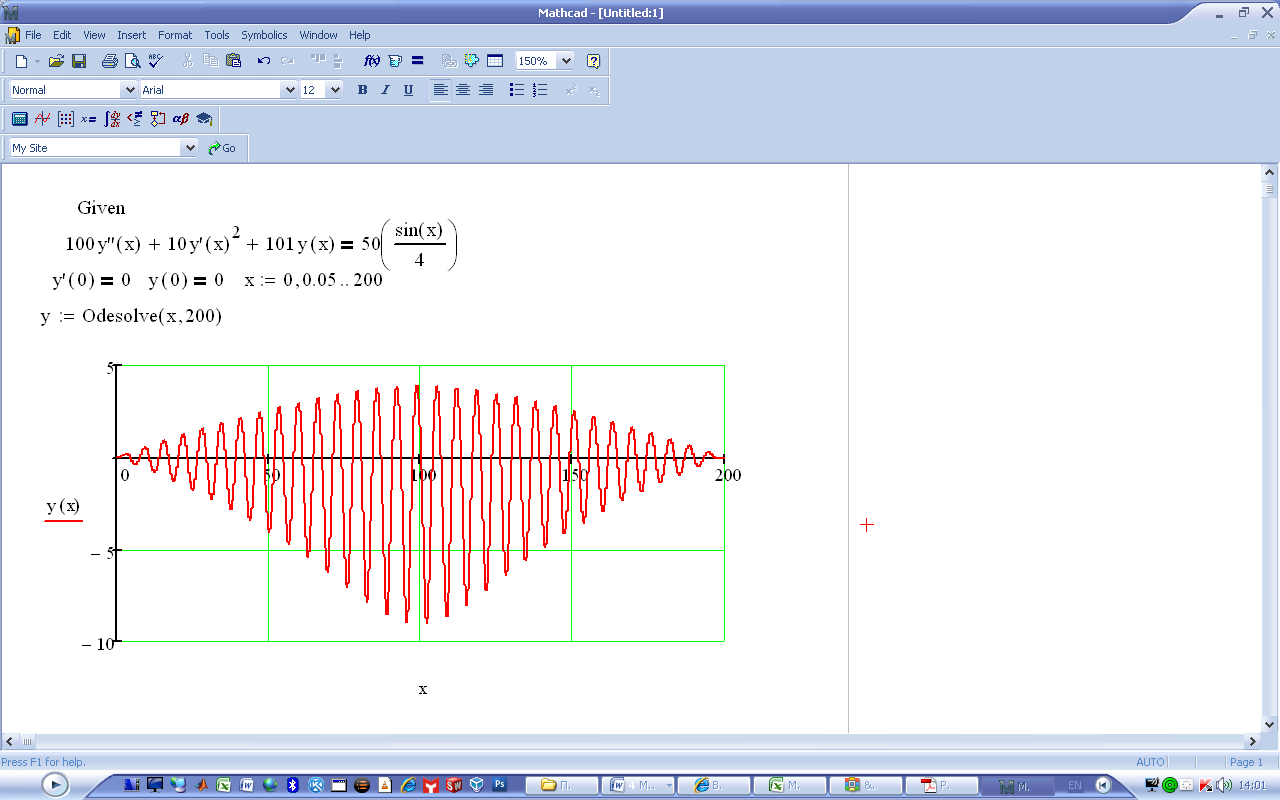
Рис.5.1. Решение в Маткаде обыкновенного дифференциального уравнения с помощью встроенной функции odesolve
Задача 2. Используя функцию odesolve, решить самостоятельно приведенные ниже дифференциальные уравнения. Построить графики решения:
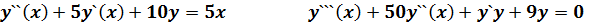


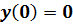
Используя функцию odesolve, можно решать и системы дифференциальных уравнений первого порядка. На рис.5.2 приведено решение системы двух уравнений.
Из рисунка видно, что в функцию odesolve помимо прежних данных вводится вектор имен решаемых функций
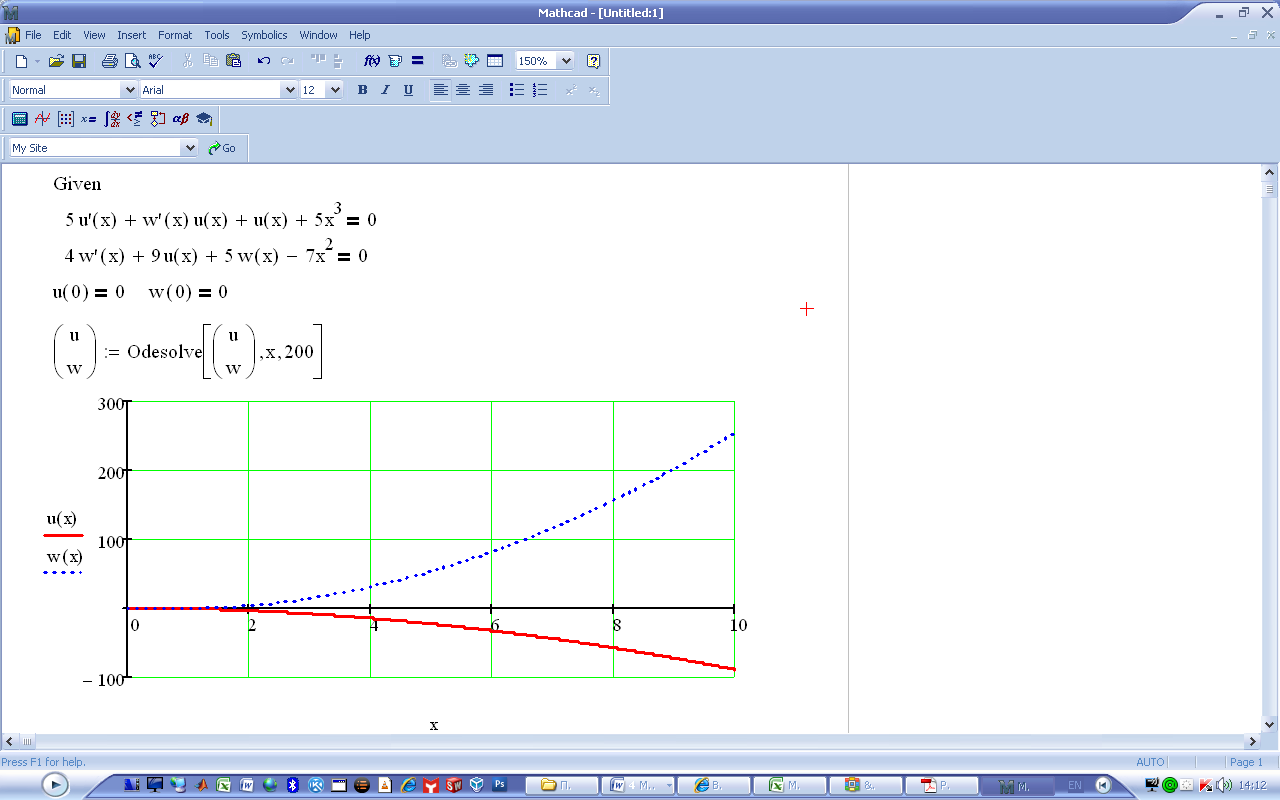
Рис.5.2.Решение системы уравнений первого порядка. Недостатком этой функции является фиксированная нижняя граница аргумента
Задача 3. Решить самостоятельно приведенную ниже систему уравнений первого порядка
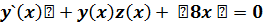
| 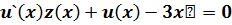
|
| z `(x)+8 z (x)−10=0 | w`(x)– w(x) + 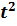 =0 =0
|
| y (0)=1 | u (0)=0 |
| z (0)=5 | w (0)=0 |
3. Решение дифференциальных уравнений с помощью функции rkfixed.
Встроенная функция rkfixed (метод Рунге – Кутта с фиксированным шагом решения) позволяет решать только системы дифференциальных уравнений первого порядка.
Уравнения порядка выше первого требуется преобразовывать в систему первого порядка. Разберем сначала, как это делается применительно к пакету Маткад.
Любое обыкновенное дифференциальное уравнение выше первого порядка может быть представлено в виде системы дифференциальных уравнений первого порядка, число которых равно порядку преобразуемого уравнения. Покажем это на примере дифференциального уравнения третьего порядка.
| Дано ay ''' +by '' +cy ' +dy=f(x). | (5.1) | |
| Введем подстановки: | ||
| y '' =y0, | (5.2) | |
| y ' =y1, | (5.3) | |
| y=y2. | (5.4) | |
| Тогда уравнение (5.1) запишется в виде: | ||
| ay0 ' +by0+cy1+dy2=f(x). (5.5) | ||
| Это первое уравнение первого порядка будущей системы. | ||
| Продифференцируем уравнение (5.3). | ||
| Получим y '' =y1 '. (5.4’) | ||
| Левые части уравнений (5.2) и (5.4’) равны. Следовательно, равны и их правые части. Отсюда | ||
| y1 ' =y0 | . (5) |
Продифференцируем уравнение (4). Получим y ' =y2 '. (5.6)
Левые части уравнений (5.3) и (5.6) равны, следовательно, равны и их правые части. Тогда
y2 ' =y1. (5.7)
Мы получили систему из трех дифференциальных уравнений первого порядка:
| ay0 ' +by0+cy1+dy2=f(x) | |
| y1 ' =y0 | (5.8) |
y2 ' =y1
Разрешив первое уравнение относительно производной, окончательно получим:
| y0 ' =–by0/a–cy1/a–dy2/a+f(x)/a | ||||||
| y1 ' =y0 | (5.9) | |||||
| y2 ' =y1 |
Решим методом Рунге- Кутты с фиксированным шагом дифференциальное уравнение второго порядка:
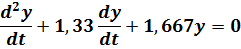
при заданных начальных условиях t0=0, y(0)=1, 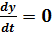 и заданном конечном счете tk=13
и заданном конечном счете tk=13
Проведя преобразование в систему уравнений первого порядка, получим:
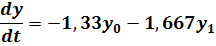
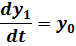
Начальные условия примут вид: y0(0) = 0, y1(0) = 1.
Записав правые части и начальные условия в виде векторов, получим
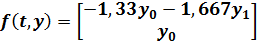

f(t, y) – это вектор правых частей системы. При его формировании его надо обратить внимание на следующее:
1.Вместо буквы f можно использовать любую другую букву. Но тогда и в
функции нужно, естественно, использовать ту же букву.
2.Внутри скобок первое имя (в нашем случае t) является именем аргумента, по которому происходит интегрирование дифференциального уравнения. Т. е. опять таки это может быть и другая буква.
3.Вторая буква внутри скобок – это вектор имен зависимых переменных. Им эти имена полностью определяются. Если принято имя y, то именами переменных должны являться y0, y1, y2 и т.д., причем первое уравнение – это
dy0 /dt =……,
второе dy1/dt = ……….. и т.д.
На рис. 5.3 приведено решение этой системы.
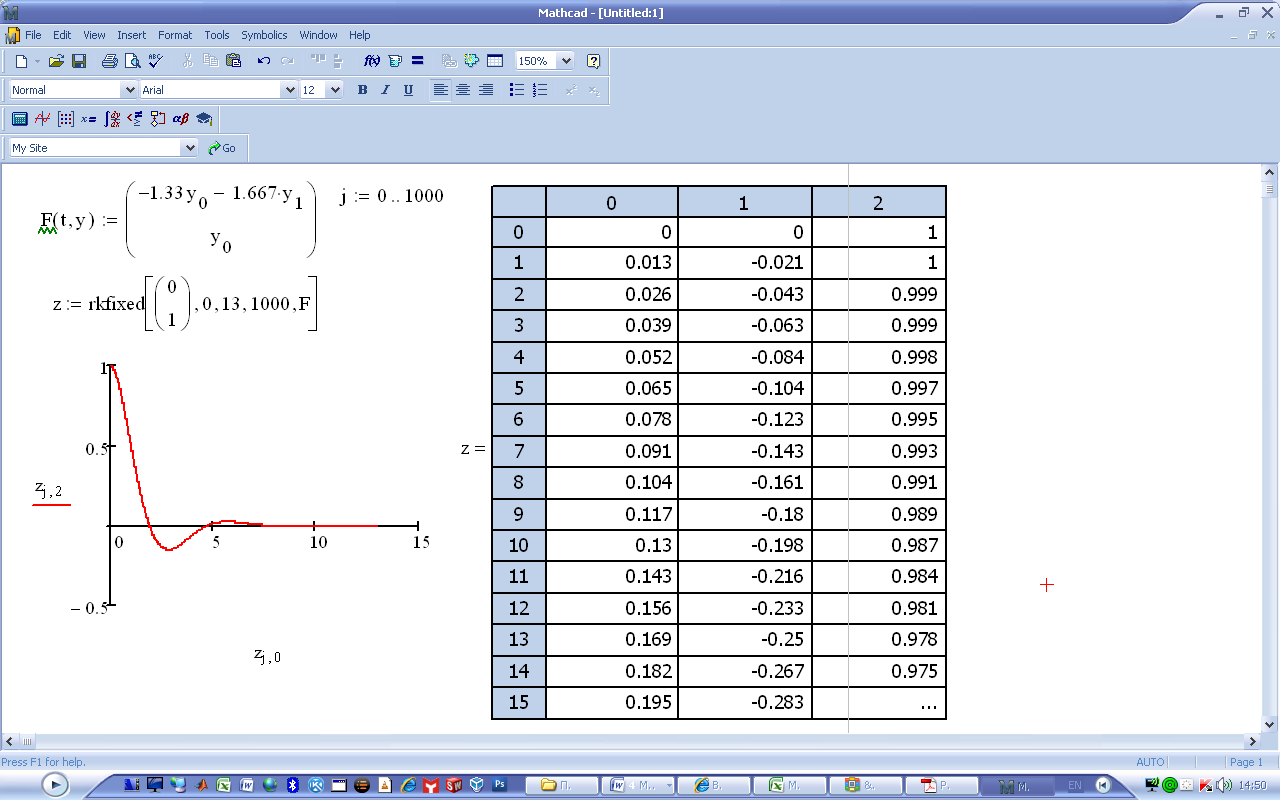
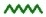
Рис.5.3 Решение дифференциального уравнения с помощью функции rkfixed.
Ответ получен в виде вектора и в виде графика. В первой строке этого вектора показаны номера переменных: z0 это время, z1 - производная y0, z2 - сама функция у. Выведены только первые 15 значений вектора ответа.
Начальные условия заданы встроенным вектором v.
Ранжировка j:= 0..1000 относится не к функции rkfixed, а к графику. Для встроенной функции число точек решения задано числом 1000 внутри нее.
Внутри функции указано время интегрирования 0 –13.
По оси абсцисс графика отложен первый столбец матрицы ответов zj,0 - аргумент (в нашей задаче – время t), где j =0..1000.
По оси ординат отложена переменная zj,2
В процессе решения задачи на экране мигает электрическая лампочка.
Контрольные вопросы
1. Ограничения функции odesolve.
2. Применение функции rkfixed к решению систем уравнений вотого и высших порядков.
ЛАБОРАТОРНАЯ РАБОТА №6 Расчет механической системы с одной степенью свободы без трения на вынужденные колебания. Составление уравнений движения систем с учетом действия возмущающей силы произвольного вида и их решение (8 часов)
Цель работы: расчет механических систем с одной степенью свободы на вынужденные колебания.
Задачи работы: приобретение практических навыков расчета механических систем с одой степенью свободы на вынужденные колебания.
Обеспечивающие средства: методика расчета механических систем с одной степенью свободы на собственные колебания.
Задание: Составление уравнений движения систем с учетом действия импульсивной нагрузки и их решение а так же с учетом действия внезапной нагрузки и их решение.
Требования к содержанию отчета: по результатам работы оформляется отчет в соответствии с порядком выполнения работы.
Порядок выполнения.
1. Уравнение движения системы с учетом демпфирования и его решение.
Для случая возмущающей силы произвольного вида сила меняется во времени не по периодическому закону. Поэтому здесь следует использовать несколько иной подход к решению задачи.
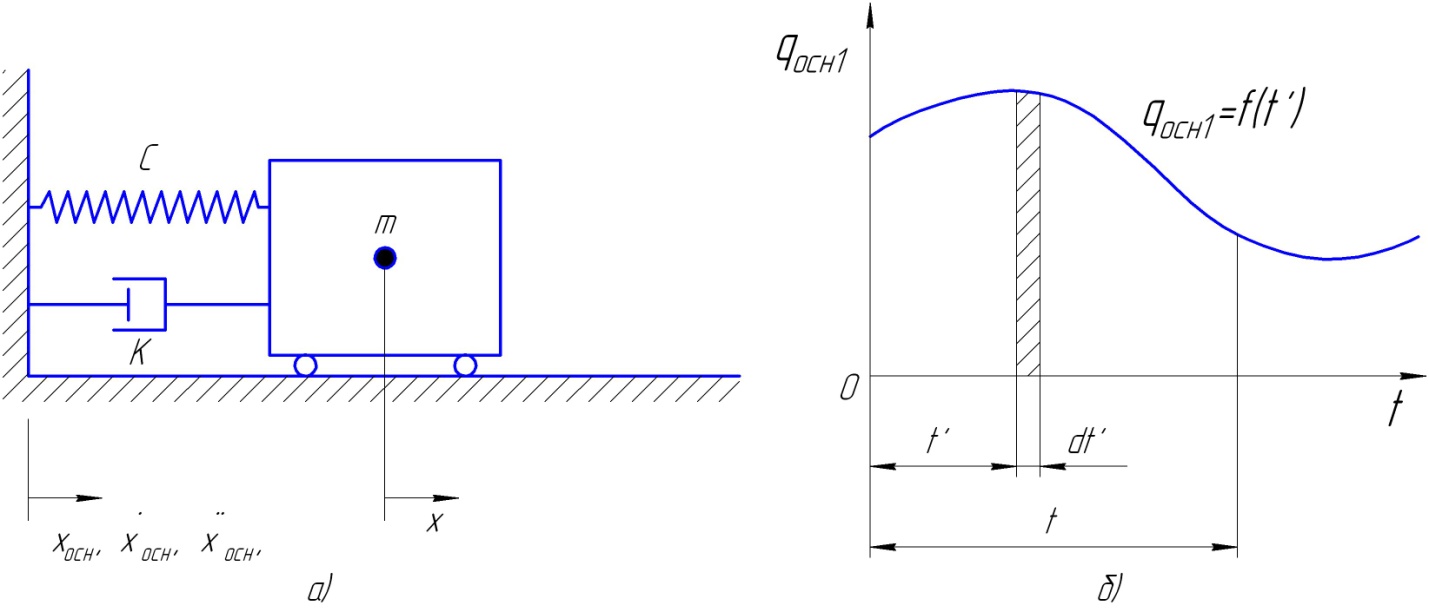
Рисунок 6.1
Рассмотрим дифференциальное уравнение движения демпфированной системы с одной степенью свободы (рис. 6.1, а) при действии возмущающей силы Q = F(t’)произвольного вида
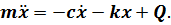
Разделив уравнение (а) на m и сделав соответствующие преобразования, получим
 (6.1)
(6.1)
где
 (б)
(б)
является возмущающей силой, отнесенной к единице массы. При выводе уравнения (6.1) предполагалось, что сила q является функцией фиктивного времени t', как показано на рис. 6.1, б. Тогда в произвольный момент времени t' можно подсчитать приращение импульса 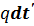 , показанное на рисунке заштрихованным прямоугольником. Этот импульс сообщает единице массы мгновенное увеличение скорости (или приращение скорости)
, показанное на рисунке заштрихованным прямоугольником. Этот импульс сообщает единице массы мгновенное увеличение скорости (или приращение скорости)
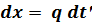 (в)
(в)
независимо от того, что на эту массу могут действовать и другие силы (например, сила упругости) и независимо от величины перемещения и скорости этой массы в момент t'. Рассматривая это приращение скорости как начальную скорость в момент t', получим, что приращение перемещения системы в любой момент времени t будет иметь вид
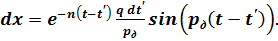 (г)
(г)
где
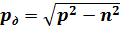 – круговая частота затухающих колебаний при демпфировании.
– круговая частота затухающих колебаний при демпфировании.
Поскольку такой же эффект вызывается каждым приращением импульса q dt' на интервале от t'=0 до t' = t, то в результате непрерывного действия возмущающей силы q получим следующее выражение для полного перемещения:
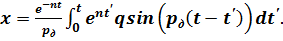 (6.2)
(6.2)
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 927; Нарушение авторских прав?; Мы поможем в написании вашей работы!