Введение 3 страница

Подобные представления в математике называются интегралом Дюамеля.

Выражение (6.2) представляет полное перемещение при действии возмущающей силы q на интервале времени от 0 до t. Оно включает как установившиеся, так неустановившиеся формы и особенно удобно при исследовании поведения системы при колебаниях, когда действует возмущающая сила произвольного вида. Если функцию q = f(t’)не представляется возможным выразить аналитически, интеграл (6.2) можно всегда вычислить приближенно с помощью соответствующего метода графического или численного интегрирования. Для того чтобы учесть влияние начального смещении и начальной скорости при t=0, необходимо только к выражению (6.2) прибавить общее решение, учитывающее указанные начальные условия. Тогда общее решение примет вид

(6.3)

2. Решение уравнения движения системы без учета демпфирования.

Если пренебречь влиянием демпфирования, получаем n = 0 и р_Д = р, в результате чего выражение (6.2) принимает вид

(6.4)

В том случае, когда учитывается влияние начального смещения х₀ и начальной скорости при t = 0, выражение (6.3) без учета демпфирования становится таким:

(6.5)

В качестве примера применения выражения (6.4) предположим, что к массе на рис. 6.1, а внезапно приложена постоянная сила Q₁ (рис. 6.2,a). Подобный характер динамического нагружения описывается так называемой ступенчатой функцией.

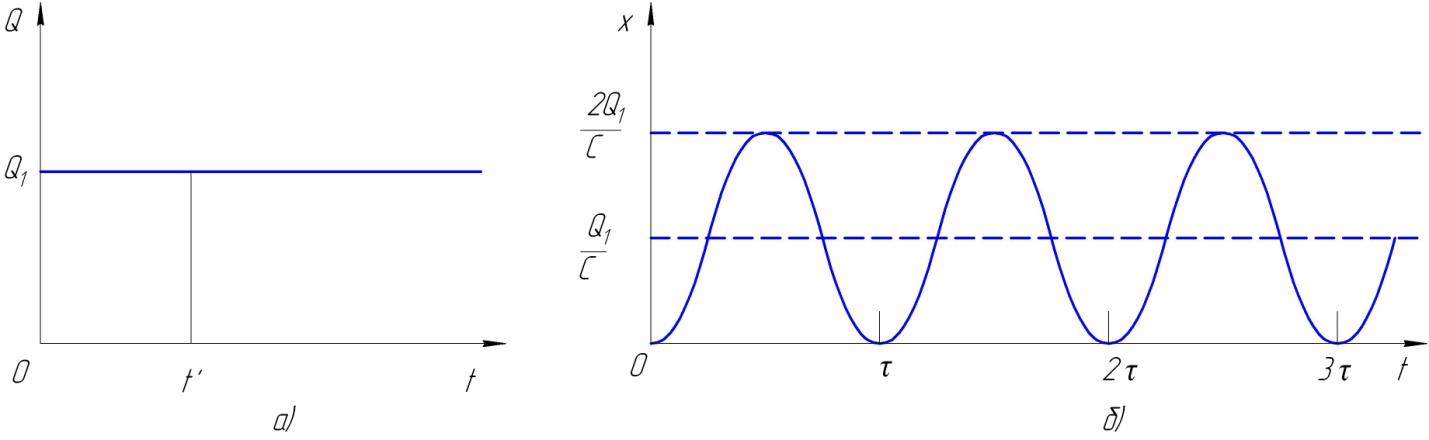
Рисунок 6.2

В этом случае имеем . Тогда выражение (6.4) примет ви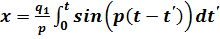д

(д)

Этот интеграл легко вычисляется, что дает

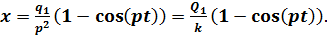(6.6)

Из приведенного решения следует, что при внезапном приложении постоянной по величине силы возникают колебания с амплитудой , наложенные на статическое смещение той же величины (рис. 6.2, б). Таким образом, максимальное перемещение, возникающее при внезапном приложении силы, в 2 раза больше перемещения, обусловленного статическим приложением силы.

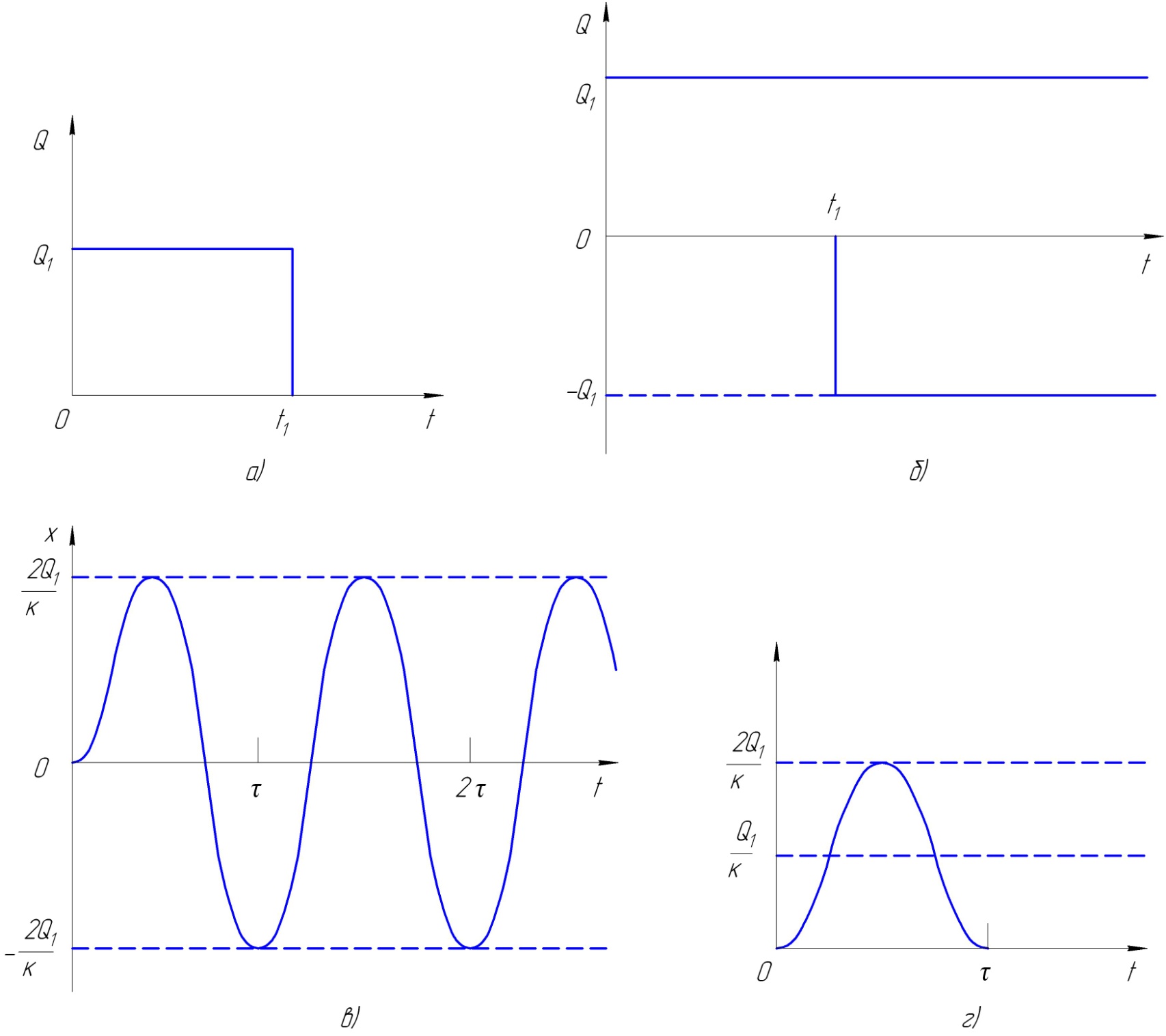
Рисунок 6.3

В рассмотренном выше случае постоянная сила Q действует в течение бесконечно большого промежутка времени. Если же она действует только на промежутке времени t₁ имеет место прямоугольный импульс (рис. 6.3). В течение времени, когда сила не равна нулю, поведение системы в точности совпадает с тем, что дается выражением (6.6). Поведение же в следующее за t₁ время можно определить с помощью интеграла Дюамеля, записанного для каждого из двух интервалов времени: от 0 до t₁ и от t₁ до t. Только интегрирование по первому интервалу дает отличный от нуля результат, поскольку во втором интервале времени функция возмущающей силы равна нулю. Суммируя сказанное, решение для рассматриваемого случая можно представить в следующем виде:

при 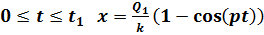_y т. е. (6.7);

при (6.8)

Исходные данные

В соответствии с расчетной схемой рисунок 6.1,а для случая внезапного приложения силы определить перемещения груза с учетом и без учета демпфирования.

№ варианта	Жесткость пружины, кН/м	Масса груза, кг	Коэффициент демпфирования, (кН·с)/м	Сила, Р, кН
			0,1
			0,2
			0,3
			0,4
			0,5
			0,6
			0,7
			0,8
			0,9
			1,1
			1,2
			1,3
			1,4
			1,5
			1,6
			1,7
			1,8
			1,9

Контрольные вопросы.

1 Дифференциальное уравнение собственных колебаний упругой системы с вязким трением.

2 Вид обшего решения дифференциального уравнение собственных колебаний упругой системы с вязким трением.

3 Период и частота собственных колебаний одномассовой системы.

4 Влияние массы тела на частоту собственных колебаний.

5 Интеграл Дюамеля.

6 Импульсивная нагрузка.

7 Внезапная нагрузка.

8 Внешняя нагрузка, изменяющаяся по гармоническому закону.

.

ЛАБОРАТОРНАЯ РАБОТА №7 Расчет механической системы с одной степенью свободы без трения на вынужденные колебания. Составление уравнений движения систем с учетом действия нагрузок, изменяющихся по гармоническому закону и их решение.(4 часа)

Цель работы: расчет механических систем с одной степенью свободы на вынужденные колебания.

Задачи работы: приобретение практических навыков расчета механических систем с одой степенью свободы на вынужденные колебания.

Обеспечивающие средства: методика расчета механических систем с одной степенью свободы на собственные колебания.

Задание: Составление уравнений движения систем с учетом действия нагрузок, изменяющихся по гармоническому закону и их решение

Требования к содержанию отчета: по результатам работы оформляется отчет в соответствии с порядком выполнения работы.

Порядок выполнения.

1. Вынужденные колебания. Установившееся состояние.

В лабораторной работе 1 были рассмотрены свободные колебания системы, состоящей из пружины и сосредоточенной массы, и показано, что движение этой системы зависит только от начальных условий её физических характеристик C и G/g, которые и определяют её частоту собственных колебаний. Если система подвергается некоторым внешним воздействиям, подобным зависящим от времени силам или специального вида движениям её опор, то динамическое поведение ее становится более сложным. Во многих практических ситуациях приходится сталкиваться с периодически изменяющимися силами, которые прикладываются к массе. Тогда реакцию системы при указанных условиях показывают вынужденными колебаниями.

В качестве примера вынужденных колебаний рассмотрим электродвигатель весом G (рис. 7.1), закрепленный на пружине, которая препятствует перемещениям только в вертикальном направлении. Эта ситуация имеет, как уже говорилось в лабораторной работе №1, круговую частоту собственных колебаний.

Предположим, что вал электродвигателя вращается с постоянной угловой скоростью со и что он недостаточно хорошо отбалансирован (на рис. 7.1 это показано в виде эксцентрической массы, сосредоточенной в точке А). Этот дисбаланс будет порождать вращающуюся центробежную силу Р, которая, в свою очередь, вызовет вынужденные колебания системы.

В дополнение к силе тяжести и силе реакции пружины теперь необходимо рассмотреть вертикальную компоненту Рsin(φt) вектора вращающейся силы. В результате получим следующее уравнение движения:

, (а)

где слагаемое Рsin(ωt) называется гармонической силовой функцией. Вводя в уравнение (а) обозначения

(б)

Получим

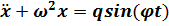. (7.1)

Частное решение этого уравнения получим, предполагая, что решение х пропорционально функции sin(φt), т. е. положив

х = A₃ sin(tω), (в)

где A₃ — постоянная, которая выбирается таким образом, чтобы решение удовлетворяло уравнению (7.1). Подставляя (в) в это уравнение, найдем A₃ =q/(p² — ω ²). Таким образом, искомое частное решение имеет вид

х = q sin ωt/(p² — ω ²). (г)

Рис. 7.1.

Рис. 7.2

Прибавляя это частное решение к общему решению однородного уравнения, получим

(7.2)

Это выражение содержит две постоянные интегрирования и является общим решением неоднородного уравнения (7.1).

Два первых слагаемых в выражении (7.2) описывают свободные колебания, которые обсуждались выше, а третье слагаемое, зависящее от возмущающей силы, характеризует вынужденные колебания системы. Можно видеть, что эти последние колебания имеют тот же период Т = 2π/ω, что и период возмущающей силы. Подставляя обо­значения (б) в выражение (г) и считая свободные колебания несущественными, получим так называемые установившиеся вынужденные колебания, описываемые выражением

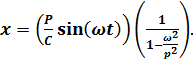(7.3)

Множитель (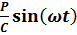) представляет собой перемещение, обусловленное действием возмущающей силы 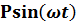, если она приложена статически; множитель 1/(1 — ²/p²) учитывает динамический характер этой силы. Абсолютная величина этого множителя обычно называется коэффициентом усиления

(д)

Видно, что коэффициент β зависит от отношения частот 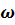/p, которое получают делением навязываемой системе частоты возмущающей силы на собственную частоту свободных колебаний системы. На рис. 7.2 представлена зависимость коэффициента β от частотного отношения 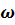/p, т. е. в случае, когда частота возмущающей силы мала по сравнению с частотой свободных колебаний, коэффициент усиления примерно равен единице, а перемещения являются почти такими же, как в случае статического действия силы Р sin( 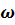t).

Когда отношение 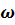/p достигает значения, равного единице, коэффициент усиления и амплитуды вынужденных колебаний быстро возрастают и обращаются в бесконечность при ω = p, т. е. в том случае, когда частота возмущающей силы совпадает с частотой свободных колебаний системы. Этот случай является условием резонанса. Бесконечное значение амплитуды вынужденных колебаний означает, что если периодическая сила действует на колеблющуюся систему всегда в соответствующее время и в соответствующем направлении, то амплитуда колебаний увеличивается, стремясь к бесконечности, при условии, что отсутствует рассеивание энергии. В практических задачах всегда имеет место рассеивание энергии, обусловленное демпфированием.

Когда частота возмущающей силы становится больше частоты свободных колебаний, коэффициент усиления вновь принимает конечное значение. Его абсолютная величина уменьшается с ростом отношения φ/ω и стремится к нулю, когда это отношение становится очень большим. Таким образом, когда на тело действует с высокой частотой периодическая сила, она вызывает колебания с очень малой амплитудой, и во многих случаях можно считать, что при этом тело сохраняет стационарное положение.

Рассматривая знак выражения 1/(1 — ω ²/p²), видим, что во всех случаях, когда выполняется условие ω < p, это выражение является положительным и перемещения массы при колебаниях имеют то же направление, что и направление возмущающей силы. С другой стороны, во всех тех случаях, когда ω > p, это выражение является отрицательным и перемещение массы имеет направление, противоположное направлению действия силы. В первом случае говорят, что колебания совпадают по фазе с возмущением, а во втором, что динамические перемещения происходят в противофазе.

В приведенном выше обсуждении величина возмущающей силы была пропорциональна sin(ωt), но те же результаты были бы получены и в том случае, если указанную силу считать пропорциональной cos(ωt). Кроме того, вынужденные колебания могут возникать и при периодических движениях опор (или движениях основания). Рассмотрим, например, подвешенный на пружине груз (рис. 1.1) и предположим, что верхнему концу пружины задано перемещение в вертикальном направлении по гармоническому закону

х_оп = d sin(ωt). (е)

Если перемещение х подвешенного груза G измерять от положения равновесия при х_оп = 0, то удлинение пружины в произвольный момент времени t будет составлять x — х_оп + δ_СТ; возникающая в пружине сила, соответствующая этому перемещению, равна C (х — х_oп) + G. Таким образом, уравнение движения подвешенного груза принимает вид

, (7.4)

Подставляя сюда выражение (е) для х_оп и используя обозначения

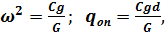(ж)

Получим уравнение

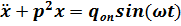. (7.5)

которое совпадает с уравнением (7.1). Следовательно, можно сделать вывод, что задание верхнему концу пружины простого гармонического перемещения dsin(ωt) эквивалентно непосредственному приложению возмущающей (kd)sin(ωt) Все приведенные выше рассуждения относительно решения уравнения (7.1) применимы также и в этом случае, и поэтому в итоге можно сделать вывод, что здесь также имеют место установившиеся вынужденные колебания, определяемые выражением

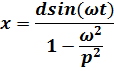
Можно принять, что числитель описывает движение сосредоточенной массы, когда перемещение опоры происходит очень медленно (или «статически»); наличие множителя 1/(1 — ω ²/ p ²) указывает на то обстоятельство, что частота перемещения опоры не равна нулю. Таким образом, для того чтобы вычислить установившуюся реакцию системы, необходимо только рассмотреть перемещение массы, обусловленное перемещением опоры.

2. Вынужденные колебания, неустановившееся состояние

Однако, благодаря влиянию затухания, неучтенного при выводе уравнения (7.2), свободные колебания исчезают в короткое время и поэтому в решении остается только та часть, которая относится к установившимся вынужденным колебаниям, постепенно поддерживаемым возбуждающей силой.

Частный случай колебаний представлен на рис. 7.3 графиком зависимости перемещений от времени. На штриховую линию, представляющую вынужденные колебания с круговой частотой накладываются свободные колебания с более высокой круговой частотой ω и уменьшающейся вследствие влияния затухания амплитудой. Таким образом, результирующее движение характеризуется сплошной линией, которая постепенно приближается к штриховой линии, относящейся к установившемуся состоянию. Начальный период этого движения, т. е. несколько первых циклов, в которых присутствуют свободные колебания, обычно называется неустановившимся состоянием. Иногда представляет практический интерес изучить этот вид движения более подробно.

Рисунок – 7.3

Амплитуду свободных колебаний можно найти из общего решения (7.2), рассмотрев начальные условия. Так же, как и в лабораторной работе №1, при t = 0 имеем х = х₀ и 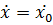. Подставляя в эти условия решение (7.2) и его производную по времени, найдем постоянные

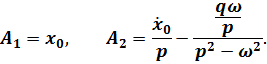
Подставляя эти постоянные в выражение (7.2), получим

. (7.6а)

Если начальные условия таковы, что это выражение упрощается до

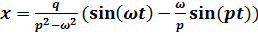. (7.6б)

Выражение (7.6б) описывает поведение во времени системы при действии возмущающей силы Psin(ωt) и состоит из двух частей. Первая относится к установившемуся движению, рассмотренному в предыдущем параграфе, и пропорциональна sin(ωt), тогда как вторая характеризует свободные колебания и пропорциональна sin(pt). Их сумма не является гармоническим движением даже тогда, когда та состоит яз двух гармонических функций, поскольку составляющие имеют различные частоты.

Если для возбуждающей силы взять функцию Pcos(ωt) вместо Psin(ωt) то е выражении (7.2) следует sin(ωt) заменить на cos(ωt); В этом случае из граничных условий получаем следующие значения постоянных:

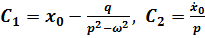(б)

Подстановка этих значении в решение дает

.

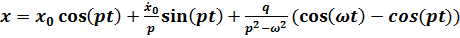Если начальные условия имеют вид примет форму

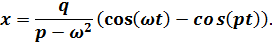
В этом случае часть характеристики системы, относящаяся к сво­бодным колебаниям, имеет ту же амплитуду, что и часть, описывающая установившееся состояние, за исключением множителя ω /p.

Особый интерес представляет случаи, когда частота функции возмущающей силы равна или очень близка к частоте свободных колебаний системы, т. е. когда ω и p близки. Исследуя этот случай, введем обозначения

p – ω = 2ε.

где ε — малая величина. Затем перепишем выражение (7.6б), описывающее реакцию при действии возмущающей силы, задаваемой функцией Psin(ωt), в следующей эквивалентной форме:

Используя тригонометрические формулы, выражение (г) можно представить в виде

Подставляя обозначения (в) в выражение (д), получим

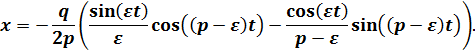
Рассматривая предел этого выражения, найдем

Вводя фазовый угол, можно записать

где

Таким образом, в предельном случае, когда ω = p, амплитуда колебания с течением времени стремится к бесконечности, как показано на рис. 7.4, где сплошная линия представляет в безразмерном виде выражение (1.31а), штриховая линия — в аналогичном виде только первое слагаемое. Можно видеть, что уже через короткое время первое слагаемое становится хорошей аппроксимацией полного динамического поведения системы, следовательно, можно принять

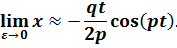
Кривые, представленные на рис. 7.4, показывают, что в системе при резонансе амплитуда вынужденных колебаний при отсутствии затухания теоретически стремится к бесконечности, для достижения которой требуется бесконечно большое время. Таким образом, при проектировании машины, в которой имеется возможность управлять упомянутым выше резонансом, не представляет большой трудности испытать ее прохождением через резонанс при условии, что этот переход осуществляется исключительно быстро. Однако, как было обнаружено экспериментально, если колеблющаяся система такова, что установившееся состояние лежит ниже зоны резонанса, то очень сложно повысить частоту вращения с тем, чтобы заставить установку пройти через зону резонанса. Дополнительная мощность, затрачиваемая для этой цели, расходуется на увеличение амплитуд колебания, а эксплуатационная частота вращения подвижных частей установки изменяется мало.

Рисунок 7.4

Когда частота функции возмущающей силы близка к частоте колебаний системы (но точно не равна), может наблюдаться явление, называемое биением. Это явление описывается выражением (е), причем достаточно хорошее приближение для динамического поведения системы получается из упрощенной формулы, включающей в себя только первое слагаемое:

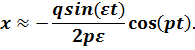
Поскольку величина ε в представлении (1.32) мала, функция sin(εt) изменяется медленно, а ее период, равный 2π/ε, является большим. Следовательно, можно считать, что представление (1.32) описывает колебания с периодом 2π/ε и переменной амплитудой, равной . Такого рода колебания нарастают и затухают в виде периодических биений, показанных на рис. 1.27. Период биения, равный π/ε, увеличивается, когда частота колебаний приближается к частоте p (т. е. при ε → 0). При резонансе период биения становится бесконечным, а рост амплитуды — непрерывным, как видно из рис. 1.26.

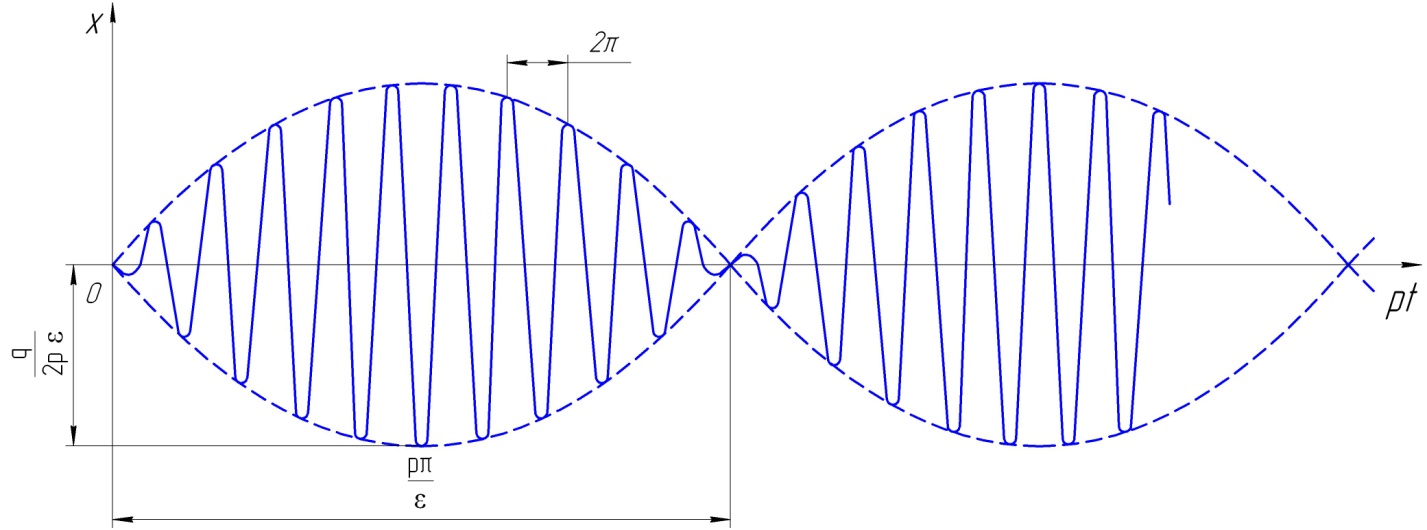
Рисунок 7.5

Исходные данные

В соответствии с рисунком 7.1 определить перемещение груза на пружине под действием гармонической нагрузки.

№ варианта	Жесткость пружины, кН/м	Масса груза, кг	Сила, Р, кН	Частота вынуждающей силы, Гц

Контрольные вопросы

1 Вид общего решения дифференциального уравнение собственных колебаний упругой системы с вязким трением.

2 Период и частота собственных колебаний одномассовой системы.

3 Влияние массы тела на частоту собственных колебаний.

4 Логарифмический декремент затухания.

5 Внешняя нагрузка, изменяющаяся по гармоническому закону.

6 Коэффициент вязкого демпфирования.

ЛАБОРАТОРНАЯ РАБОТА №8 Расчеты на удар.(6 часов)

Цель работы: расчет механических систем на удар при осевом действии нагрузки, а так же при изгибе.

Задачи работы: приобретение практических навыков расчета механических систем с на удар.

Обеспечивающие средства: методика расчета механических систем на удар.

Требования к содержанию отчета: по результатам работы оформляется отчет в соответствии с порядком выполнения работы.

Порядок выполнения.

1. Расчет на удар при осевом действии нагрузки

С явлением удара приходится иметь дело в том случае, когда скорость рассматриваемого элемента конструкции или соприкасающихся с ним частей в очень короткий промежуток времени изменяется на конечную величину. Получающиеся при этом большие ускорения (замедления) приводят к возникновению значительных инерционных сил, действующих в направлении, противоположном направлению ускорений, т. е. в направлении движения тела. В случае падающего груза величина силы удара (динамической силы ) может быть вычислена по формуле

(8.1)

где Q — вес падающего груза;

g — ускорение свободного падения;

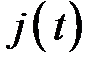— ускорение падающего груза после соприкосновения его с препятствием.

Дата добавления: 2014-12-07