Вычисления с использованием арифметики произвольной точности 2 страница

ans =

-1+(1/2*pi)^(1/2*pi)

>> vpa(ans,5)

ans =

1.0327

Найденное решение неверное, т. к. оно не прошло проверку подстановкой.

Команда solve может возвратить не все решения.

Пример:

Решить трансцендентное уравнение sinx+lnx+e^x - 1 = 0.

Решение:

>> syms x

>> Y=sin(x)+log(x)+exp(x)-1;

>> S=solve(Y);

>> vpa(S,5)

ans =

-3.0553-1.7145*i

>> subs(Y,S)

ans =

-.8e-31-.1e-30*i

Возвратив приближенный комплексный корень уравнения x₁ = -3,0553 - 1,7145i, solve не нашла вещественный корень. С помощью команды ezplot (см. раздел 15) графически определяем, что он находится вблизи значения 0,4 (рисунок 2):

>> ezplot('sin(x)+log(x)+exp(x)-1',[0,1,-1, 3])

>> grid

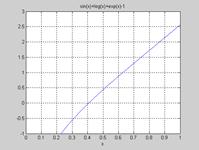
Рисунок 2

Вещественный корень x₂=0,4072 найден в [2] (раздел 6.2) с помощью команды fzero.

Перейдем теперь к системам уравнений.

Пример:

Решить систему уравнений

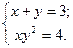
Решение:

Результатом выполнения команды solve является структура S с полями x и y, каждое из которых содержит символьное представление решения:

>> syms x y

>> Y1=x+y-3;

>> Y2=x*y^2-4;

>> S=solve(Y1,Y2,x,y)

S =

x: [3x1 sym]

y: [3x1 sym]

Выведем в командное окно содержимое структуры:

disp([S.x S.y])

[ 4, -1]

[ 1, 2]

[ 1, 2]

Получили три решения (x₁;y₁) = (4; -1) и (x₂;y₂) = (1;2) (второе – кратности 2), причем (x₁;y₁) хранится в [ S.x(1) S.y(1) ], а (x₂;y₂) – в [ S.x(2) S.y(2) ]:

>> disp([S.x(1) S.y(1)])

[ 4, -1]

>> disp([S.x(2) S.y(2)])

[ 1, 2]

Для проверки подставим в выражения Y1 = x+y - 3 и Y2 = xy² - 4 вначале первое решение, а затем второе:

>> disp(subs([Y1 Y2],[x y],[S.x(1) S.y(1)])

[ 0, 0]

>> disp(subs([Y1 Y2],[x y],[S.x(2) S.y(2)])

[ 0, 0]

Как видим, найдены точные решения, т. к. выражения Y1 и Y2 при их подстановке обратились в 0.

Команда solve допускает использование символьных переменных в качестве выходных аргументов. Эквивалентное обращение к solve в предыдущем примере имеет вид:

>> [x,y]=solve(Y1,Y2,x,y)

x =

[ 4]

[ 1]

[ 1]

y =

[ -1]

[ 2]

[ 2]

Команда solve позволяет решать системы уравнений, заданные в аналитическом виде.

Пример:

Решить систему уравнений относительно x, y, z

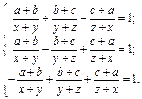
Решение:

>> syms a b c x y z

>> Y1=(a+b)/(x+y)+(b+c)/(y+z)-(c+a)/(z+x)-1;

>> Y2=(a+b)/(x+y)-(b+c)/(y+z)+(c+a)/(z+x)-1;

>> Y3=-(a+b)/(x+y)+(b+c)/(y+z)+(c+a)/(z+x)-1;

>> S=solve(Y1,Y2,Y3,x,y,z)

S =

x: [1x1 sym]

y: [1x1 sym]

z: [1x1 sym]

>> disp([S.x S.y S.z])

[ a, b, c]

Проверим найденное решение (a;b;c) подстановкой в систему:

>> subs([Y1 Y2 Y3],[x y z],[S.x S.y S.z])

ans =

[ 0, 0, (-a-b)/(a+b)+1]

>> disp(simplify(ans))

[ 0, 0, 0]

Убеждаемся, что решение найдено верно.

Иногда системе MATLAB можно помочь, преобразовав уравнение или систему уравнений к эквивалентному виду.

Например, уравнение ln(4 - 2x)+x² - 2 = 0 имеет эквивалентный вид e^2−x²+2x - 4 = 0. Можно проверить, что для каждого из этих уравнений команда solve возвращает свой вещественный корень. Это будут разные корни, но каждый из них удовлетворяет исходному уравнению. Существует и третий вещественный корень, который можно найти с помощью команды fzero [2].

Пример:

Решить систему трансцендентных уравнений

Решение:

>> syms x y

>> Y1=3^y*9^x-81;

>> Y2=log10((y+x)^2)-log10(x)-2*log10(3);

>> S=solve(Y1,Y2,x,y)

S =

x: [4x1 sym]

y: [4x1 sym]S =

>> R=[S.x S.y];

>> disp(vpa(R,10))

[ 16.00000002, -28.00000004]

[ 16.00000002, -3.999999992]

[ 1.000000000, -3.999999996]

[ 1.000000000, 1.999999996]

Получили 4 приближенных решения c 10 значащими цифрами. Однако системе удовлетворяют только первое и последнее из них. Убедимся в этом подстановкой:

>> disp(vpa(subs([Y1,Y2],[x y],[S.x(1) S.y(1)]),15))

[.1e-12,.15e-13]

>> disp(vpa(subs([Y1,Y2],[x y],[S.x(2) S.y(2)]),15))

[ 22876792454891.6,.25e-13]

>> disp(vpa(subs([Y1,Y2],[x y],[S.x(3) S.y(3)]),15))

[ -80.8888888888889,.31e-13]

>> disp(vpa(subs([Y1,Y2],[x y],[S.x(4) S.y(4)]),15))

[ -.71e-11,.18e-13]

Приближенное равенство [ Y1,Y2 ] » [ 0,0 ] выполняется только при подстановке в систему первого и последнего решений. В остальных случаях [ Y1,Y2 ] ≠ [ 0,0 ].

Алгебраическими преобразованиями приведем исходную систему к эквивалентной системе

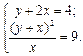
Решим ее:

>> syms x y

>> S=solve('y+2*x=4','(y+x)^2/x=9',x,y);

>> [S.x S.y]

ans =

[ 1, 2]

[ 16, -28]

Получили два точных решения, являющихся также решениями исходной системы.

Пример:

Решить cистему уравнений

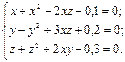
Решение:

>> syms x y z

>> Y1=x+x^2-2*y*z-.1;

>> Y2=y-y^2+3*x*z+.2;

>> Y3=z+z^2+2*x*y-.3;

>> S=solve(Y1,Y2,Y3,x,y,z);

>> R=[S.x S.y S.z];

>> disp(vpa(R,6))

[ -.541941+.626019e-1*i, -.179057-.433417*i,.148543-.344892*i]

[ -.541941-.626019e-1*i, -.179057+.433417*i,.148543+.344892*i]

[.128241e-1, -.177801,.244688]

[ -1.08804, -.130325,.161425e-1]

[.578802e-1,.156279e-1, -1.24040]

[.374678+.356411*i,.353227-.580416*i, -.281751+.419593*i]

[.374678-.356411*i,.353227+.580416*i, -.281751-.419593*i]

[.121093, 1.17493,.152166e-1]

Получено 8 приближенных решений с 6 значащими цифрами, 4 из которых вещественные (c 3 - го по 5 - е и 8 - е). Проверим все 8 решений подстановкой с помощью цикла for [2]:

>> for i=1:8

T=subs([Y1 Y2 Y3],[x y z],[S.x(i) S.y(i) S.z(i)]);

disp(vpa(T,6))

end

[ -.5e-31-.1471e-30*i, -.32e-30+.71e-30*i,.25e-30+.103e-29*i]

[ -.5e-31+.1471e-30*i, -.32e-30-.71e-30*i,.25e-30-.103e-29*i]

[.12e-30,.9e-31, -.13e-30]

[.8e-31,.14e-30, -.3e-31]

[.2e-31, -.6e-31, -.14e-30]

[.637e-29+.829e-29*i, -.754e-29+.15e-30*i,.709e-29-.346e-29*i]

[.637e-29-.829e-29*i, -.754e-29-.15e-30*i,.709e-29+.346e-29*i]

[.17422e-27, -.1012e-28,.12735e-27]

При подстановке любого из решений [ Y1 Y2 Y3 ] » [ 0 0 0 ]. Значит, каждое из них удовлетворяет системе уравнений.

13 РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ – КОМАНДА dsolve

Для решения обыкновенных дифференциальных уравнений (систем уравнений) MATLAB имеет команду

r = dsolve('eq1','eq2',...,'cond1','cond2',...,'v').

Она возвращает аналитическое решение дифференциальных уравнений eq1, eq2,..., использующих v как независимую переменную, с граничными и (или) начальными условиями cond1, cond2,.... По умолчанию независимой переменной считается переменная t, обычно обозначающая время. Если в выражениях eqI (condI) не используется знак равенства, то полагается, что eqI (condI) = 0.

Символ D обозначает производную по независимой переменной, то есть d/dt, при этом D2 означает d²/dt² и т. д. Имя независимой переменной не должно начинаться с буквы D.

Начальные условия задаются в виде равенств 'y(a) = b' или 'Dy(a) = b', где у – зависимая переменная, a и b – константы, которые могут быть и символьными. Могут быть символьными и константы в уравнениях. Если число начальных условий меньше порядка уравнения, то в решении будут присутствовать произвольные постоянные C1, C2 и т. д. Формы вывода результата такие же, как и для команды solve. Справку по dsolve можно получить, введя команду doc dsolve.

Пример:

Решить дифференциальные уравнения

1) x'' = -2x', 2) y'' = -ax+y', y(0) = b, 3) y⁽⁴⁾ - y = 5e^xsinx+x⁴, 4) y''+4y'+3y = cost, y(0) = 1, y'(0) = 0.

Решения 3 - го и 4 - го уравнений проверить подстановкой.

Решение:

>> dsolve('D2x=-2*x')

ans =

C1*cos(2^(1/2)*t)+C2*sin(2^(1/2)*t)

>> dsolve('D2y=-a*x+y','y(0)=b','x')

ans =

a*x+C1*sinh(x)+b*cosh(x)

>> syms x

>> S=dsolve('D4y-y-5*exp(x)*sin(x)-x^4','x');

>> [R]=simple(S)

R =

-24-x^4-exp(x)*sin(x)+C1*exp(x)+C2*sin(x)+C3*cos(x)+C4*exp(-x)

Проверка 3-го решения:

>> diff(R,x,4)-R-5*exp(x)*sin(x)-x^4

ans =

>> S=dsolve('D2y+4*Dy+3*y=cos(t)','y(0)=1','Dy(0)=0','t')

S =

1/10*cos(t)+1/5*sin(t)-7/20*exp(-3*t)+5/4*exp(-t)

Проверка 4-го решения:

>> syms t

>> diff(S,t,2)+4*diff(S,t)+3*S

ans =

cos(t)

Проверка выполнения начальных условий 4 - го решения:

>> subs(S,t,0)

ans =

>> subs(diff(S,t),t,0)

ans =

Пример:

Решить систему линейных дифференциальных уравнений

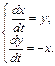
Решение:

>> S=dsolve('Dx = y', 'Dy = -x')

S =

x: [1x1 sym]

y: [1x1 sym]

>> disp([S.x, S.y ])

[ cos(t)*C1+sin(t)*C2, -sin(t)*C1+cos(t)*C2]

Пример:

Решить систему линейных дифференциальных уравнений с начальными условиями и проверить решение

Решение:

>> S=dsolve('Dx = y', 'Dy = -x','x(0)=1','y(0)=2')

S =

x: [1x1 sym]

y: [1x1 sym]

>> disp([S.x S.y])

[ cos(t)+2*sin(t), -sin(t)+2*cos(t)]

Получено решение: x = cost+2sint, y = -sint+2cost.

Проверка решения:

syms t

>> diff(S.x,t)-S.y

ans =

>> diff(S.y,t)+S.x

ans =

Проверка выполнения начальных условий:

>> subs(S.x,t,0)

ans =

>> subs(S.y,t,0)

ans =

Команда dsolve не позволяет получить аналитическое решение дифференциального уравнения произвольного вида.

Пример:

Найти аналитическое решение уравнения Ван-дер-Поля

y'' - (1 - y²)y'+y = 0, y(0) = 2, y'(0) = 0.

Решение:

Обращение к dsolve выдает сообщение о том, что решение не найдено:

>> dsolve('D2y-(1-y^2)*Dy+y=0','y(0)=2','Dy(0)=0')

ans =

[ empty sym ]

В некоторых случаях dsolve возвращает решение, выраженное через специальные функции.

Пример:

Найти аналитическое решение уравнения Бесселя

x²y''+xy'+(x² - v²)y = 0.

Решение:

>> dsolve('x^2*D2y+x*Dy+(x^2-v^2)*y=0','x')

ans =

C1*besselj(v,x)+C2*bessely(v,x)

Решение выражается через функции Бесселя. Информацию о функциях Бесселя можно получить с помощью команды doc besselj.

14 ПРЯМОЕ И ОБРАТНОЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА – КОМАНДЫ laplace, ilaplace

Преобразование Лапласа любой комплексной функции f(t) действительной переменной t имеет вид

L(s) = f(t)e^-stdt.

Функцию f(t) принятоназывать оригиналом, а функцию L(s) – изображением. Функция f(t) должна удовлетворять следующим условиям:

а) f(t) является непрерывной функцией для всех значений t, принадлежащих области определения. (Допускается наличие разрывов первого рода в конечном числе точек, расположенных на интервалах конечной длины. Количество таких интервалов должно быть конечным числом);

б) f(t) = 0 при t < 0;

в) существуют числа M > 0 и p ≥ 0 такие, что для всех t │ f(t) │ < Me^pt (p называется показателем роста │ f(t) │).

Некоторые простейшие преобразования Лапласа приведены в таблице 7.1.

Таблица 1 − Некоторые преобразования Лапласа

f(t)	L(s) = f(t)e^-stdt.
1	s^-1
e^-at	(s+a)^-1
sinat	a(s^2+a^2)^-1
t^n	n!s^-n-1
e^-atcoswt
t^ne^-at

В MATLAB преобразование Лапласа функции f(t) осуществляется с помощью команды laplace(F,t,s).

Найдем с помощью этой команды изображения заданных в таблице 1 оригиналов f(t):

>> syms a t w s

>> n=sym('n','positive');

>> laplace(1,t,s)

ans =

1/s

>> laplace(exp(-a*t),t,s)

ans =

1/(s+a)

>> laplace(sin(a*t),t,s)

ans =

a/(s^2+a^2)

>> laplace(t^n,t,s)

ans =

s^(-n-1)*gamma(n+1)

>> laplace(exp(-a*t)*cos(w*t),t,s)

ans =

(s+a)/((s+a)^2+w^2)

>> laplace(t^n*exp(-a*t),t,s)

ans =

gamma(n+1)*(s+a)^(-n-1)

Полученные изображения совпадают с табличными, если учесть, что

gamma(n+1) = n! для целых n (см. раздел 10).

Пример:

Найти изображение функции f(t) = e^-2tsin2tcos3t.

Решение:

>> syms t s

>> laplace(exp(-2*t)*sin(2*t)*cos(3*t),t,s)

ans =

5/2/((s+2)^2+25)-1/2/((s+2)^2+1)

>> pretty(ans)

1 1

5/2 ------------- - 1/2 ------------

2 2

(s + 2) + 25 (s + 2) + 1

>> factor(ans)

ans =

2*(s^2+4*s-1)/(s^2+4*s+29)/(s^2+4*s+5)

>> pretty(ans)

s + 4 s - 1

2 ------------------------------

2 2

(s + 4 s + 29) (s + 4 s + 5)

Итак,

L(s) = 2.

Пример:

Найти изображение функции f(t) =.

Решение:

При обращении к laplace команда возвращается без результата:

>> laplace(1/t,t,s)

ans =

laplace(1/t,t,s)

Это означает что либо изображения не существует, либо системе MATLAB не удалось его найти.

Существуют различные модификации laplace (справку можно получить с помощью команды doc laplace).

Обратное преобразование Лапласа имеет вид

f(t) = L(s)e^stds.

В среде MATLAB обратное преобразование Лапласа функции L(s) можно получить с помощью команды ilaplace(L,s,t). Найдем с ее помощью оригиналы заданных в таблице 1 изображений L(s):

>> syms a t w s

>> n=sym('n','positive');

>> ilaplace(1/s,s,t)

ans =

>> ilaplace(1/(s+a),s,t)

ans =

exp(-a*t)

>> ilaplace(a/(s^2+a^2),s,t)

ans =

a/(a^2)^(1/2)*sin((a^2)^(1/2)*t)

>> ilaplace(s^(-n-1)*gamma(n+1),s,t)

ans =

t^n

>> ilaplace((s+a)/((s+a)^2+w^2),s,t)

ans =

exp(-a*t)*cos(w*t)

>> ilaplace(gamma(n+1)*(s+a)^(-n-1),s,t)

ans =

exp(-a*t)*t^n

Полученные оригиналы совпадают с табличными.

Пример:

Найти оригинал полученного ранее изображения

2

функции f(t) = e^-2tsin2tcos3t.

Решение:

>> syms t s

>> ilaplace(2*(s^2+4*s-1)/(s^2+4*s+29)/(s^2+4*s+5),s,t)

ans =

1/2*exp(-2*t)*sin(5*t)-1/2*exp(-2*t)*sin(t)

>> factor(ans)

ans =

1/2*exp(-2*t)*(sin(5*t)-sin(t))

Поскольку (sin5t - sint) = sin2tcos3t, то оригинал найден верно.

Пример:

Найти оригинал изображения

L(s) =.

Решение:

Команда ilaplace возвращает решение, выраженное через функцию Хевисайда:

>> syms t s a

>> ilaplace(exp(-2*s)/(s+a),s,t)

ans =

Heaviside(t-2)*exp(-a*(t-2))

Функция Хевисайда (единичная функция) определяется следующим образом:

δ₀(t) =

Следовательно, найденный оригинал имеет вид

f(t) =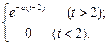

Пример:

Найти оригинал изображения

L(s) =.

Решение:

Команда ilaplace возвращает решение, выраженное через корни уравнения z⁴+1 = 0:

>> syms t s

>> ilaplace((s^4-1)/(s^5+s),s,t)

ans =

-1+2*sum(1/4*exp(_alpha*t),_alpha = RootOf(_Z^4+1))

Команда vpa вычисляет приближенное значение оригинала с заданным количеством текущих цифр:

>> vpa(ans,4)

ans =

-1.+1.000*exp(-.7071*t)*cos(.7071*t)+1.000*exp(.7071*t)*cos(.7071*t)

Пример:

Найти оригинал изображения

L(s) =.

Решение:

Команда ilaplace возвращается без результата:

>> syms t s

>> ilaplace(exp(2*s)/(s+3)^2,s,t)

ans =

ilaplace(exp(2*s)/(s+3)^2,s,t)

Это означает что либо оригинала не существует, либо системе MATLAB не удалось его найти.

Существуют и другие модификации ilaplace (справку можно получить, введя команду doc ilaplace).

15 ГРАФИКИ СИМВОЛЬНЫХ ФУНКЦИЙ – КОМАНДЫ ezplot, ezpolar

Чтобы избавить пользователя от хлопот, связанных с построением графиков функций с помощью стандартных средств (например, команды plot, [2]), в пакет Symbolic введены довольно удобные графические команды класса ezplot:

ezplot(f) – строит график символьно заданной функции f(x) независимой переменной x в интервале[- 2*pi;2*pi ];

ezplot(f,xmin,xmax) – делает то же, но позволяет задать диапазон изменения независимой переменной x в интервале от xmin до xmax;

ezplot(f, [xmin, xmax, ymin, ymax]) – строит график функции f(x,у) = 0 для xmin < х < xmax, ymin < y < ymax.

Построим график функции sin(t)/t (рисунок 3):

>> ezplot('sin(t)/t'),grid

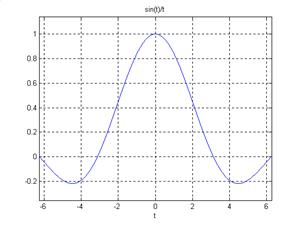
Рисунок 3

Следующая команда строит график гиперболы u² - v² - 1 = 0 для - 3 < u < 3, - 3 < v < 3 (рисунок 4):

>> ezplot('u^2-v^2-1',[-3, 3, -3, 3]),grid

Рисунок 4

Ранее с помощью команды ezplot был построен график на рисунке 2.

График функции f(t) в полярной системе координат строит команда ezpolar:

ezpolar(f) – строит график функции f(t) при изменении угла t от 0 до 2π;

ezpolar(f,[a b]) – строит график функции f(t) при изменении угла t от a до b.

Построим график функции cos3t в полярной системе координат (рисунок 5):

>> ezpolar('cos(3*t)')

Рисунок 5

Помимо команд ezplot и ezpolar, пакет Symbolic поддерживает построение графиков других типов. Так, команда ezcontour служит для построения контурных графиков функций вида f(x,y). Похожая команда ezcontourf строит контурные графики с функциональной окраской областей между линиями равного уровня. Для построения трехмерных графиков параметрически заданных функций служит команда ezplot3. Команды ezsurf, ezsurfc, ezmesh, ezmeshc применяются для построения графиков поверхностей, заданных функциями двух переменных f(x,y). Справку с примерами по применению любой из этих команд можно получить с помощью команды doc < имя команды >.

16 ПРЯМОЙ ДОСТУП К ЯДРУ СИСТЕМЫ Maple – КОМАНДА maple

Применение возможностей системы Maple совместно с возможностями системы MATLAB придает последней особую гибкость и резко расширяет возможности решения сложных математических задач, где целесообразно объединять аналитические (символьные) методы с численными расчетами.

Доступ к большинству функций и команд системы Maple, ядро которой включено в МАТLAB, осуществляется командой maple.

Пример:

Найти аналитическое решение дифференциального уравнения y''+2xy'+ny = 0.

Решение:

Обращение к dsolve приводит к решению, выраженному через функции Уиттекера:

>> dsolve('D2y+2*x*Dy+n*y=0','x')

ans =

C1/x^(1/2)*WhittakerW(1/4*n-1/4,1/4,x^2)*exp(-1/2*x^2)+C2/x^(1/2)*WhittakerM(1/4*n-1/4,1/4,x^2)*exp(-1/2*x^2)

Непосредственно из МАТLAB функции WhittakerW и WhittakerM недоступны, т.к. их нет в списке mfunlist функций системы Maple, доступных из МАТLAB [2].

Определение функций функций Уиттекера, варианты вызова и подробное описание с примерами использования возвращает команда mhelp Whittaker. Вычислим значение одной из них:

>> maple('WhittakerM(1,2,3)')

ans =

WhittakerM(1,2,3)

>> vpa(ans,7)

ans =

10.17605

Ниже приводятся примеры решения в МАТLAB некоторых математических задач с привлечением возможностей системы Maple.

Дата добавления: 2014-12-07