
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вопросы для самопроверки. 1. Как создать символьную переменную в matlab.
|
|
|
|
1. Как создать символьную переменную в MATLAB?
2. Как в MATLAB осуществляется управление точностью вычислений?
3. Как выполняются в MATLABупрощения и подстановки в символьных выражениях?
4. Как в MATLAB вычислить в символьном виде значение предела функции?
5. Как выполнить в MATLABдифференцирование в символьном виде?
6. Как вычислить в MATLABзначение интеграла в символьном виде?
7. Как получить в MATLABв символьном виде разложение функции в ряд?
8. Как вычислить в MATLABзначение суммы и произведения ряда в символьном виде?
9. Как можно в MATLAB найти решение алгебраического уравнения в символьном виде?
10. Как можно в MATLAB найти решение дифференциального уравнения в символьном виде?
11. Как осуществляется в MATLAB в символьном виде прямое и обратное преобразование Лапласа?
12. Перечислите встроенные в MATLAB средства визуализации символьных вычислений?
13. Как можно в MATLAB обратится к ядру системы Maple?
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
За номером задания в скобках указан раздел, после которого выполняется задание.
Задание 1 (8). Найти предел.
Требуется найти предел функции.
Варианты
1. 2. 3.
4. 5. (1+3tg2x)ctg2x 6.
7. 8. 9. (tgx)tg2x 10.
11. 12. 13. (sinx)tgx
14. 15.
Задание 2 (9). Найти производные.
Найти первые и вторые частные производные функции двух переменных f(x,y). Проверить выполнение условия f''xy(x,y) = f''yx(x,y). Вычислить градиент функции f(x,y) в точке (1;2).
Варианты
1. f(x,y) = arctg(x+y) 2. f(x,y) = arcsin(lnxy) 3. f(x,y) = e-xlny
4. f(x,y) = cos(e-xlny) 5. f(x,y) = ln(lnxy) 6. f(x,y) = sinxcosy
7. f(x,y) = arcctg 8. f(x,y) = arccos(sin(x-y)) 9. f(x,y) = elnxy
10. f(x,y) = arccos 11. f(x,y) = arcctg(ex-ey)
12. f(x,y) = xln(x+y) 13. f(x,y) = ln 14. f(x,y) = arcsin(ex+y)
15. f(x,y) = ycos(xy)
Задание 3 (10). Найти неопределенный интеграл.
Найти неопределенный интеграл dx. Воспользоваться при необходимости командами pretty, simple.
Варианты
1. 2. dx 3. dx 4. 56. dx 7. dx
8. dx 9. 10.
11. dx 12. 13.
14. dx 15. dx
Задание 4 (10).Вычислить определенный интеграл.
Вычислить определенный интеграл dx. Воспользоваться при необходимости командой vpa.
Варианты
1. 2. dx 3. 4. dx
5. 6. 7. dx 8.
9. 10. 11.
12. 13. 14. 15.
Задание 5 (10). Вычислить кратный определенный интеграл.
Вычислить кратный определенный интеграл. Воспользоваться при необходимости командой vpa.
Варианты
1. cos(x2–y2+sinz)dxdydz 2. (x2+y)coszdxdydz
3. (x2+y2)dxdy 4. xsin(yz)dxdydz 5. cos(xyz)dxdydz
6. arcsin(xy)dxdy 7. sin(x–y2+z)dxdydz
8. (x2+y2)(z+y)dxdydz 9. arccos(x2+y2)dxdy
10. arcsin(x+yz)dxdydz 11. (x+y)(z+y)(z+x)dxdydz
12. arcsin(x2y2)dxdy 13. arccos(x–y)dxdy
14. tg(xy+z)dxdydz 15. xycoszdxdydz
Задание 6 (11). Разложить функцию в ряд Тейлора.
Разложить функцию f(x) в ряд Тейлора по степеням x-a. Воспользоваться при необходимости командами pretty, simple. Исследовать с помощью команды taylortool приближение функции на интервале [ –2π+a;2π+a ] отрезком ряда Тейлора, содержащем различное число членов разложения.
Варианты
1. f(x) =, a=0 2. f(x) = (1–x2)cosx, a=0 3. f(x) = 2x, a=3
4. f(x) =, a=–2 5. f(x) =, a=0 6. f(x) = e3x, a=1
7. f(x) = excosx, a=0 8. f(x) =, a=2 9. f(x) =, a=0
10. f(x) = (arctgx)2, a=0 11. f(x) = exln(10+x), a=0
12. f(x) = x2sinx, a=0 13. f(x) = e-xsinx, a=0
14. f(x) = ln(x+), a=0 15. f(x) = cos2x, a=0
Задание 8 (12). Решить систему алгебраических уравнений.
Решить с помощью команды solve систему алгебраических уравнений, проверить решение подстановкой.
Варианты
1. 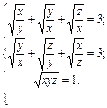 2.
2. 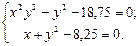 3.
3. 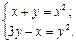 4.
4. 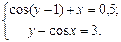 5.
5. 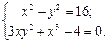 6.
6. 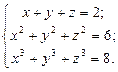
7. 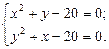 8.
8. 
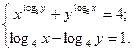 9.
9. 
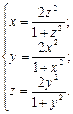 10.
10. 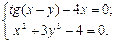 11.
11. 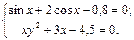 12.
12. 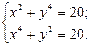
13. 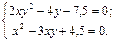 14.
14. 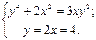 15.
15. 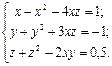
Задание 9 (13). Решить дифференциальное уравнение или
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 420; Нарушение авторских прав?; Мы поможем в написании вашей работы!