Ламинарном движении

Законы гидравлического сопротивления при

Одним из наиболее простых видов движения вязкой жидкости является ламинарное движение в цилиндрической трубе, а в особенности его частный случай - установившееся равномерное движение. Теория ламинарного движения жидкости основывается на законе трения Ньютона. Это трение между слоями движущейся жидкости является единственным источником потерь энергии.

Рассмотрим установленное ламинарное течение жидкости в прямой трубе с d=2 r₀

Чтобы исключить влияние силы тяжести и этим упростить вывод допустим, что труба расположена горизонтально.

Пусть в сечении 1-1 давление равно P₁ а в сечении 2-2 – P_2.

Ввиду постоянства диаметра трубы V =const, 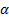= const, тогда уравнение Бернулли для выбранных сечений примет вид:

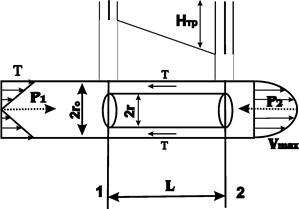
Рис. 11 Ламинарное движение жидкости в трубе

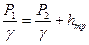
отсюда ,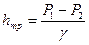

что и будут показывать пьезометры, установленные в сечениях.

В потоке жидкости выделим цилиндрический объем.

Запишем уравнение равномерного движения выделенного объема жидкости, то есть равенство 0 суммы сил, действующих на объем.

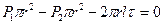
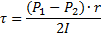
Отсюда следует, что касательные напряжения в поперечном сечении трубы изменяются по линейному закону в зависимости от радиуса. Эпюра касательного напряжения 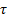показана на рис. 11 слева.

Если выразить касательное напряжение t по закону Ньютона, то будем иметь

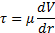
Знак минус обусловлен тем, что направление отсчета r (от оси к стенке противоположного направления отсчета y (от стенки)

Подставив значение t в предыдущее уравнение, то получим^

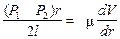
Отсюда найдем приращение скорости:

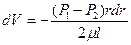
Выполнив интегрирование получим.

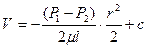
Постоянную интегрирования c найдем из условия, что на стенке

r =r_0; V = 0

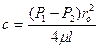
Скорость по окружности радиусом r \ равна

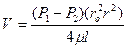
Это выражение является законом распределения скорости по сечению круглой трубы при ламинарном течении. Кривая, изображающая эпюру скоростей, является параболой второй степени. Максимальная скорость, имеющая место в центре сечения при r=0 равна

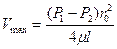
Применим полученный закон распределения скоростей для расчета расхода.

dQ =V dS

Площадку dS целесообразно взять в виде кольца радиусом r и шириной dr

Тогда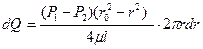

После интегрирования по всей площади поперечного сечения, то есть от r =0, до r = r₀

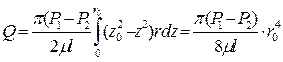
Для получения закона сопротивления выразим; (через предыдущую формулу расхода)

(

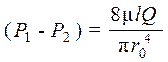µ=υρ r₀= d/2 γ= ρg. Тогда получим закон Пуарейля;

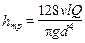
Полученная формула закона сопротивления показывает, что при ламинарном течении в трубе круглого сечения потеря напора на трение пропорциональна расходу и вязкости в первой степени и обратно пропорциональна диаметру в четвертой степени. Этот закон, часто называемый законом Пуайзеля, используется для расчета трубопроводов с ламинарным течением.

Как показывают опыты, во многих, но не во всех случаях гидравлические потери примерно пропорциональны квадрату скорости течения жидкости. Поэтому в гидравлике принят следующий общий способ выражения гидравлических потерь полного напора в линейных единицах

.

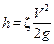Такое выражение удобно тем, что включает в себя безразмерный коэффициент пропорциональности ζ, называемый коэффициентом сопротивления, и скоростной напор, входящий в уравнение Бернулли. Коэффициент сопротивления ζ, таким образом, есть отношение потерянного напора к скоростному напору.

С учетом введенного определения в формуле (16) заменим расход через произведение 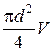и после сокращения запишем:

.

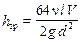Умножив и разделив на 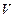и перегруппировав множители, получим

.

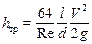Обозначив через 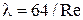гидравлический коэффициент сопротивления трения, потеря напора будет равна

.

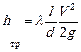Полученная формула носит название формулы Дарси-Вейсбаха. Потеря напора на трение при ламинарном течении пропорциональна скорости в первой степени. Квадрат скорости в формуле (8.20) для ламинарного течения получен искусственно умножением и делением на 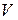, а коэффициент λ обратно пропорционален 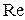и, следовательно, скорости 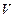. Из выражения (8.19) следует, что для вычисления потери напора при ламинарном движении надо знать всего лишь одну величину – коэффициент вязкости жидкости, есл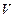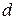и , и 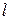заданы. Род материала, из которого изготовлены трубы, а также шероховатость стенок трубы не оказывают влияния на величину потери напора.

Дата добавления: 2014-12-07