Идеальной жидкости

Уравнение Бернулли для элементарной струйки

ОСНОВНЫЕ УРАВНЕНИЯ ДИНАМИКИ ЖИДКОСТИ

Основное уравнение кинематики

Из последнего уравнения следует, что средние скорости в потоке несжимаемой жидкости обратно пропорциональных площадям живых сечений

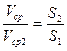
Вопросы для самопроверки:

1. Что изучают в разделе «Основы кинематики»?

2. Какие движения (потоки) жидкости называются напорными и безнапорными?

3. Какое движение жидкости называется установившимся (стационарным)?

4. Какое движение жидкости называется неустановившимся (нестационарным)?

5. В чём состоит особенность в задании поля скоростей по Эйлеру?

6. Что представляет собой струйчатая модель потока жидкости (газа)? Из каких элементов она состоит?

7. Какие два вида ускорения имеют место в общем случае движения жидкости, и с какими силами эти ускорения связаны?

Изучаемые вопросы:

- Дифференциальное уравнение гидродинамики идеальной жидкости.

- Уравнение Бернулли для установившегося напорного движения идеальной жидкости.

-Уравнение Бернулли для потока реальной (вязкой) жидкости

Обратимся к интегрированию дифференциальных уравнений Эйлера для движения идеальной жидкости.

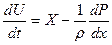
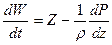
За время dt частица жидкости переместится вдоль элементарной струйки на расстояние ds. (Проекция ds на оси координат dx, dy, dz)

1. Умножим каждое из уравнений на dx, de, dz и сложим

При установившемся движении P = f (x, y, z), поэтому выражение в скобках есть полный дифференциал давления, выраженный через частные производные dP.

Зная, что ; ;

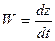
есть проекции скоростей от координат движущейся точки, получим:

;

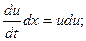
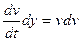или

Тогда уравнение можно записать в следующем виде:

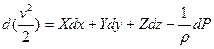
Предположим, что из объемных сил действует лишь сила тяжести, а ось z направлена вертикально вверх, тогда Х=0, Y=0, Z= - q, тогда последнее уравнение примет вид

в

Или разделив на –q и зная, что ρq = γ, будем иметь

Проинтегрировав это уравнение получим:

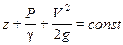
Z - геометрическая высота (напор)

P/γ – пьезометрическая высота (напор) – удельная потенциальная энергия потока (удельно-отнесенная к единице массы).

V²/2g – скоростной напор – удельная кинетическая энергия потока

Все члены уравнения Бернулли имеют линейную размерность.

Z – отметка – высота рассматриваемого живого сечения струй над плоскостью сравнения.

p/γ – пьезометрическая высота, отвечающая гидродинамическому давлению в точке и является высотой столба жидкости в пьезометре.

С физической точки зрения уравнение Бернулли представляет собой закон сохранения механической энергии. Механическая энергия движущейся жидкости может иметь 3 формулы: 1, энергия положения Z, энергия давления P/γ и кинетическая энергия V²/2g.

«В процессе движения идеальной жидкости одна форма энергии может превращаться в другую, однако полная удельная энергия остается без изменений».

H =Z + P/γ + V²/2g – полный напор = const

Дата добавления: 2014-12-07