Векторные линии и траектории

Векторной линией в поле векторов называется линия, в каждой точке которой в данный момент времени вектор касателен к ней.

Совокупность векторных линий, проходящих через все точки некоторого контура, образует векторную поверхность.

Если рассматривать движение жидкой частицы во времени, то линия, по которой двигалась частица в некоторый момент времени называется траекторией.

Траектории частиц жидкости при установившемся течении являются неизменными во времени.

При неустановившемся течении траектории различных частиц, проходящих через данную точку пространства, могут иметь разную форму. Поэтому для рассмотрения картины течения, возникающей в каждый момент времени, вводится понятие линии тока.

Линией тока называется кривая, в каждой точке которой вектор скорости в данный момент времени направлен по касательной.

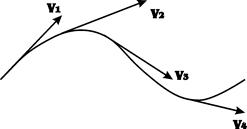
Рис. 10 Линия тока

Для установившегося движения тока, совпадает с траекторией частицы и не изменяет своей формы с течением времени.

Если в движущейся жидкости взять бесконечно малый замкнутый контур и через все его точки провести линии тока, то образуется трубчатая поверхность называемая трубкой тока.

Часть потока, заключенная внутри трубки тока, называется элементарной струйкой.

Рис.11 Элементарная струйка

Элементарная струйка обладает следующими свойствами:

1) форма элементарной струйки остается неизменной во времени, так как линия тока с течением времени не меняет своей формы;

2) поверхность элементарной струйки является непроницаемой для частиц жидкости, поскольку жидкие частицы скользят по линии тока;

3) скорости и давления для всех точек поперечного сечения струйки следует считать одинаковыми, так как площадь этого сечения бесконечно мала.

Различают напорные и безнапорные течения жидкости. Напорными называют течения в закрытых руслах без свободной поверхности, а безнапорными – со свободной поверхностью.

При стремлении поперечных сечений размеров струйки к 0 она в пределе стягивается в линию тока. Если взять ряд “жестких” элементарных струек, то их совокупность образует поток жидкости. Площадью живого сечения, или живым сечением потока называется площадь сечения потока, проведенная нормально к направлению линий тока. Строго говоря, живые сечения потока в ряде случаев являются криволинейными, однако практически их принимают плоскими и нормальными к общему направлению движения. Часть периметра живого сечения, по которому поток соприкасается с ограничивающими его стенками, называют смоченным периметром.

Живым сечением или просто сечением потока, называется в общем случае поверхность в пределах потока, проведенная нормально к линиям тока. Далее будем рассматривать в потоках такие участки, в которых струйки можно считать параллельными, и следовательно, живые сечения плоскими.

Расходом называется количество жидкости, протекающей через живое сечение потока (струйки) в единицу времени.

Для элементарной струйки, имеющей бесконечно малые площадки сечений, можно считать истинную скорость V одинаковой во всех точках каждого сечения, тогда элементарный расход, проходящий через площадку dS выразится так dS = VdS [м³/c]

Для потока конечных размеров в общем случае скорость имеет различное значение в разных точках сечения, поэтому расход надо определять как сумму элементарных расходов струек.

Q=SVdS

Основываясь на законе сохранения вещества, на предположение о сплошности (неразрывности) течения и на непроницаемости трубки тока можно утверждать, что расходство всех сечениях элементарной струйки одинаков.

dQ=V₁dS₁=V₂dS₂=const – (вдоль струйки)

Для потока конечных размеров, ограниченного непроницаемыми стенками следует ввести средние скорости

Q=V_срS₁=V_срS₂=const – (вдоль потока)

Дата добавления: 2014-12-07