Поле скоростей и ускорений

Движение сплошной среды характеризуется прежде всего скоростями ее частиц. В каждый момент времени они имеют определенную по величине и направлению скорость.

Если поле скоростей и давлений остается неизменным во времени, то движение называется установившимся.

В случае установившегося движения давление и скорость могут изменяться при перемещении частицы жидкости из одного положения в другое, но в данной неподвижной относительно русла точке давление и скорость являются функциями только координат.

P = f₁ (x, y, z)

V = f₂ (x, y,z)

В случае неустановившегося течения давления и скорость зависят как от координат, так и от времени.

P = F₁ (x, y, z, t)

V = F₂ (x, y, z, t)

В практике часто пользуются понятиями средн. скоростей. Обычно усреднение скорости производится либо по времени, либо по площади некоторого сечения потока.

Среднее значение величины скорости за промежуток времени t₀ представляет собой интеграл:

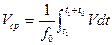
Средняя величина скорости по некоторой площади S определятся как

Вектор ускорения жидкой частицы, движущейся со скоростью V является индивидуальной производной по времени от вектора скорости:

Т.к. вектор скорости в общем случае зависит от времени и координат V = V (x, y, z, t), то по правилу дифференцирования сложной функции найдем:

Т.к. производные от координат движущейся точки по времени есть соответствующие проекции скоростей, т.е.

; ;

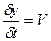получим:

В проекциях на оси координат x, y, z это уравнение будет иметь вид:

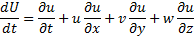
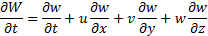
Первое слагаемое первой части равенства выражаем изменение скорости во времени в некоторой фиксированной точке пространства, т.е местное изменение и поэтому называется локальной составляющей ускорения. Остальные слагаемые характеризуют изменение скорости частицы при ее перемещении и называются конвективными составляющими ускорения.

При установившемся движении локальное ускорение всегда равно 0. при неустановившемся оно может обращаться в 0 лишь тогда, когда в данной точке скорость имеет max или min значение во времени.

Конвективное ускорение может быть при установившемся и неустановившемся движениях. Оно обращается в 0 лишь тогда, когда средняя скорость не зависит от координат.

Движение называется равномерным, если скорость частиц не меняется вдоль их траекторий, в противном случае – движение неравномерное. Течение жидкости может быть установившимся и неустановившимся. Если величина скорости и ее направление, а также давление в данной точке пространства одинаковы в течение всего процесса протекания жидкости, то такое движение называется установившимся. При неустановившемся же движении жидкости поле скоростей и поле давлений будут непрерывно изменяться. Линии тока и траектории частиц жидкости совпадают между собой только при установившемся движении, так как при этом являются неизменными во времени.

Дата добавления: 2014-12-07