Высотные сети сгущения 3 страница

здесь 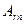- матрица коэффициентов уравнений поправок размером 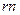( 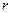строк и 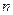столбцов); 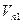- вектор поправок размером 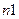( 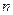строк, 1 столбец); -вектор невязок размером 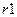( 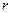строк, 1 столбец).

Условие минимума суммы квадратов поправок записывается так .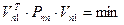

Система нормальных уравнений коррелат имеет вид

,

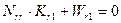где 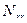- матрица коэффициентов нормальных уравнений коррелат, 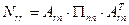; 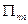- матрица обратных весов измеренных элементов, 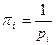; 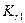- вектор коррелат размером 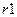. Поправки в измерения выражаются через коррелаты по формуле

.

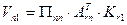Применим изложенную теорию коррелатного способа уравнивания к уравниванию нивелирного хода.

Веса измеренных превышений 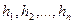вычисляют по длине секций 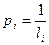; эта формула получается из следующих рассуждений: за ошибку единицы веса 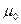примем ошибку измерения превышения на пути в 1 км и обозначим среднюю квадратическую ошибку i -того превышения через 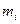, тогда имеем последовательно

, , .

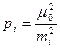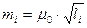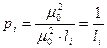Иногда за ошибку единицы веса принимают среднюю квадратическую ошибку измерения превышения на пути в 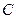километров; тогда 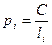. Если принять 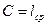, то в этом случае различия весов измеренных превышений будут наименьшими, что в теории уравнивания играет положительную роль.

В нивелирном ходе всего одно условие

,

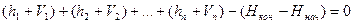которое линейно относительно поправок 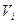, поэтому условное уравнение поправок будет

;

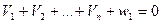невязка 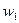подсчитывается по формуле

.

Сначала выразим обратные веса через длины секци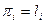й и .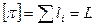

Затем напишем нормальное уравнение одной коррелаты и учтём, что ,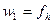

,

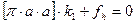откуда 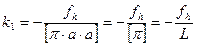, так как 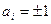, и .

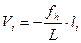Уравненные значения измеренных превышений вычисляем по формуле 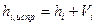, затем вычисляем уравненные значения отметок определяемых реперов

.

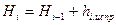При уравнивании нивелирного хода III класса следует учесть, что в нём превышения по секциям измеряются дважды - в прямом и обратном направлениях, поэтому

;

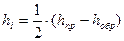в этой формуле учтено, что прямое превышение 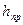и обратное превышение 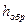имеют противоположные знаки, а при вычислении среднего превышения ему приписывают знак прямого превышения. Кроме того, вычисляют расхождения прямого и обратного превышений 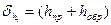и сравнивают их с допустимыми значениями

.

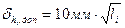Оценка точности нивелирного хода III класса выполняется по формулам

, , , ,

, .

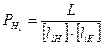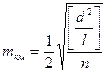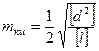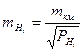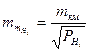Приведём вывод формулы веса уравненной отметки репера. Отметку репера можно вычислить дважды: от начального исходного репера и от конечного исходного репера; затем из этих двух значений следует взять средне-весовое, вес которого будет равен сумме весов этих двух отметок.

Вес первой отметки вычисляется по формуле

;

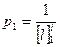в знаменателе стоит расстояние от начального исходного репера до определяемого репера.

Вес второй отметки вычисляется по формуле

;

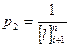в знаменателе стоит расстояние от конечного исходного репера до определяемого репера.

Далее пишем

.

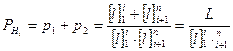Обработка нивелирного хода III класса выполняется в специальной ведомости, форма которой приведена в “Лабораторном практикуме” по геодезии.

2.6.2. Обработка нивелирной сети с одной узловой точкой

В связи с широким внедрением компьютеров в практику геодезических вычислений исчезла актуальность "ручных" способов обработки сложных нивелирных сетей, и в настоящее время обработка нивелирных сетей выполняется на ПК по программам, в которых реализованы алгоритмы строгого МНК-уравнивания.

Из применяемых в прежние времена "ручных" способов: - способ эквивалентной замены, способ узлов, способ полигонов, - особый теоретический интерес представляет первый способ, в котором путем несложных вычислений нивелирная сеть с несколькими узловыми точками может быть преобразована в сеть с одной узловой точкой. В способе узлов и способе полигонов уравнивание выполняется методом приближений; оба они были разработаны русским учёным геодезистом В.В. Поповым.

Пусть в репере 1 сходятся n ходов; длины ходов обозначим через 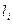, измеренные превышения по ним - через 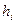(рис.18). Отметку репера 1 можно получить 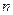раз (на рис.18 ):

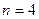Рисунок 18 – Схема нивелирной сети с одной узловой точкой

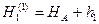- из 1-го хода,

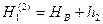- из 2-го хода,

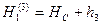- из 3-го хода,

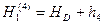- из 4-го хода.

При разной длине ходов 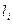ошибки превышений по ходам также различны, следовательно, отметки 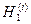будут получены с разными весами, и для вычисления средней отметки репера 1 нужно применить формулу весового среднего

,

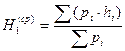где 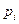- вес i -того хода; 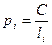( 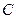- константа).

После вычисления сеть разделяется на четыре изолированных одиночных хода, каждый из которых обрабатывается по известной методике.

2.6.3. Обработка нивелирной сети по способу эквивалентной замены

Идея способа эквивалентной замены заключается в том, что два нивелирных хода, сходящихся в одной точке, можно заменить одним эквивалентным ходом, вес которого равен сумме весов составляющих его двух ходов, и превышение по которому равно средне-весовому из превышений двух ходов. Рассмотрим нивелирную сеть, изображенную на рис.19.

Рисунок 19 – Схема нивелирной сети

Сначала заменим ходы 1 и 2 одним эквивалентным ходом , вес которого равен

.

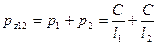Длину хода выразим через длины ходов 1 и 2

.

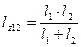Отметка репера 1, вычисленная по превышениям ходов 1 и 2 или из эквивалентного хода , будет равна

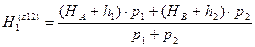
После первой замены вид сети изменится (рис.20).

Рисунок 20 – Вид нивелирной сети после первой замены

Следующим шагом будет "сложение" хода с ходом 3; эквивалентный им ход обозначим ; его длина будет

.

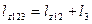Отметка репера 2, полученная из ходов 1, 2, 3 или из эквивалентного хода , будет равна

.

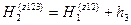Вес отметки репера 2, полученной из эквивалентного хода , будет равен

.

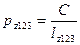Вид нивелирной сети после второй эквивалентной замены изображён на рис.21.

Рисунок 21 – Схема нивелирной сети после второй замены

В узловой точке - репере 2, - сходятся три хода, и дальнейшая обработка сети выполняется по методике обработки нивелирной сети с одной узловой точкой, описанной выше, то есть,

, , , , .

.

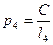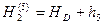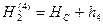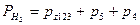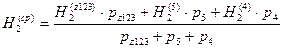Поправки 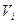в измеренные превышения получают по следующим формулам

; ; ;

; ; ; .

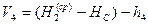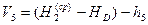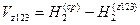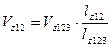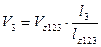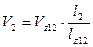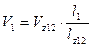Оценка точности уравненной нивелирной сети заключается в вычислении средней квадратической ошибки единицы веса 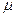, средней квадратической ошибки превышения на один километр хода 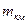и ошибок отметок реперов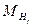

,

,

.

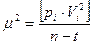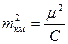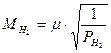В этих формулах: 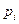- вес i -того хода; 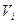- поправка из уравнивания в превышение по i -тому ходу; 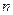- количество ходов в сети (количество измеренных превышений); 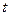- количество определяемых реперов в сети; 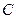- константа при вычислении весов, как правило 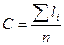; 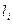- длина i -того хода; 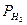- вес репера 2.

Чтобы получить вес репера 1, нужно уравнять сеть заново, заменяя ходы 4 и 5 эквивалентным ходом и затем “складывая” ход 3 и полученный эквивалентный ход. В результате таких замен узловым репером, в котором будут сходиться три хода, должен стать репер 1.

Для нивелирных сетей сложной формы разработаны методики эквивалентной замены “звезда - треугольник”, “треугольник - звезда” и другие. Как отмечается в литературе, такие замены интересны прежде всего с теоретической точки зрения, а практически они очень громоздки и неудобны, а потому способ эквивалентной замены рекомендуется применять для обработки или предрасчёта точности небольших по размерам и относительно простых по форме нивелирных сетей.

2.6.4. Обработка нивелирной сети по способу узлов

Рассмотрим ту же ниверную сеть (рис.18), в которой исходными данными являются отметки 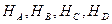реперов A,B,C,D, измерены пять превышений 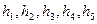по пяти ходам 1, 2, 3, 4 и 5; определяемыми данными являются отметки 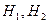реперов 1 и 2.

Идея способа заключается в вычислении отметок 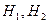по измеренным превышениям, сходящимся в реперах 1 и 2 соответственно

,

.

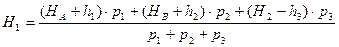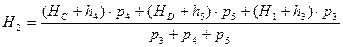Вес каждого хода подсчитывается по известной формуле

,

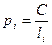где 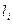- длина хода в километрах, а 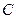- средняя длина хода в сети (тоже в километрах). При уравнивании сети по способу узлов удобнее пользоваться приведёнными весами

;

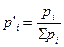сумма приведённых весов на определяемом репере должна быть равна 1,000.

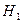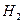Поскольку отметки и неизвестны, то в первом приближеннии отметка 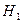вычисляется по неполной формуле – без третьего слагаемого в числителе и знаменателе; при вычислении отметки 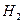в первом приближении отметка 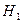берётся из первого приближения. При дальнейших приближениях каждый раз берётся последнее вычисленное значение той и другой отметок.

Приближения заканчиваются, когда различие обеих отметок 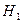и 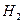в последнем и предпоследнем приближениях (в общем случае всех определяемых отметок) не превышает один миллиметр.

Оценка точности в способе узлов затруднена из-за трудностей при определении весов уравненных отметок определяемых реперов. Поправки в первое измеренное превышение вычисляется по формуле 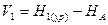, во второе – по формуле 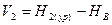и так далее. Затем вычисляется средняя квадратическая ошибка единицы веса

.

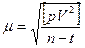Веса отметок определяемых реперов можно вычислить по формулам В.П.Козлова; приближённо вес отметки определяемого репера равен сумме весов ходов, сходящихся в нём. Формулы В.П.Козлова предполагают вычисление весов отметок реперов двумя приближениями. В первом приближении вес отметки репера равен сумме весов нивелирных ходов, сходящихся в данном репере минус несколько поправочных членов; количество таких членов равно количеству нивелирных линий, сходящихся в репере, а каждый член равен дроби, в числителе которой стоит квадрат веса нивелирной линии, а в знаменателе – сумма весов нивелирных линий, сходящихся в репере на конце данной линии; если на конце линии находится исходный репер, то данный член равен нулю.

,

.

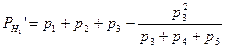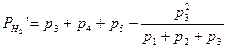Во втором приближении в знаменателе каждого члена вместо суммы весов нивелирных линий нужно поставить вес отметки репера в конце линии, полученный из первого приближения.

,

.

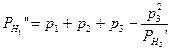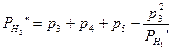2.6.5. Обработка нивелирной сети по способу полигонов

В способе полигонов, называемом также способом красных чисел, выполняется последовательное распределение невязок каждого полигона пропорционально весам нивелирных ходов, входящих в полигон. Этот способо соответствует решению нормальных уравнений коррелат в коррелатном способе уравнивания МНК методом последовательных приближений.

Сначала намечают замкнутые полигоны, количество которых должно быть равно количеству избыточных измерений в сети; при необходимости в полигон включают ход между исходными реперами, превышение по которому считается истинным и не получает поправку при уравнивании.

Затем для каждого полигона, вычисляют высотные невязки 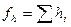, где 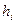- измеренные превышения по ходам полигона; знаки превышений должны соответствовать направлению, единому для всей нивелирной сети, например, по часовой стрелке. Кроме того, для всех ходов полигона подсчитывается так называемые красные числа по формуле 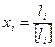; 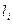- длина хода, 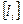- периметр полигона (сумма длин всех ходов полигона); красные числа вычисляются до 0,001; сумма красных чисел в полигоне должна быть равна 1,000.

В каждом полигоне строят колонки: одну – для записи первичной невязки и приведённых невязок; и несколько колонок по числу ходов полигона – для записи поправок; эти колонки располагают за пределами полигона около каждой его стороны (рис.22). На этом рисунке сеть состоит из трёх исходных реперов, восьми нивелирных ходов и трёх определяемых реперов. Количество полигонов равно 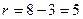. В первом полигоне колонка невязок обозначена римской цифрой I; для трёх ходов полигона за его пределами построены три колонки поправок; все они обозначены арабской цифрой 1. Аналогичные построения выполнены и для остальных четырёх полигонов.

Обход полигонов начинают с полигона, невязка в котором имеет наибольшее значение, например, с полигона I; невязка этого полигона (-60мм) распределяется пропорционально красным числам трёх его ходов (0,250; 0,350; 0,400) и записывается в миллиметрах в колонки с обозначением 1. Затем переходят ко второму полигону; подсчитывается его приведённая невязка, равная первичной невязке и поправки, поступившей в полигон от невязки первого полигона (+45мм – 21мм = +24мм). Эта приведённая невязка (+24мм) распределяется в два хода и записывается в колонки поправок с обозначением 2. Дальнейшие действия выполняют по той же методике.

Выполнив первый обход, приступают ко второму обходу, в котором приведённые невязки подсчитываются как суммы поправок, поступивших в полигон при последнем распределении невязок. Как только приведённые невязки во всех полигонах станут равными нулю, процесс обхода заканчивается.

Рисунок 22 – Схема уравнивания нивелирной сети по способу полигонов

Поправка в измеренное превышение по ходу, входящему только в один полигон, равна сумме поправок в колонке данного хода; знак поправки зависит от направления хода и направления при вычислении невязок: при совпадении направлений знак поправки одинаков со знаком суммы, при противоположных направлениях знак поправки обратен знаку суммы.

Поправка в измеренное превышение по смежному ходу (входящему в два полигона) равна разности сумм поправок в двух колонках; знак поправки определяется по тому же правилу направлений.

После вычисления поправок в измеренные превышения заполняют таблицу вычисления отметок реперов, вычисляют среднюю квадратическую ошибку единицы веса, веса уравненных отметок реперов и их средние квадратические ошибки. Веса отметок реперов можно вычислить, как и в способе узлов, по формулам В.П.Козлова.

2.6.6. Обработка нивелирной сети параметрическим способом МНК

В параметрическом способе МНК-уравнения приняты следующие обозначения:

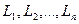- измеренные величины (превышения) с весами соответственно 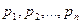; количество измеренных превышений равно ;

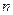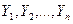- уравненные значения превышений;

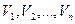- поправки из уравнивания к измеренным превышениям; связь уравненных превышений, поправок в измерения и измеренных превышений выражается формулой

;

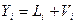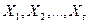- определяемые неизвестные (отметки реперов); их количество равно 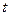, причём .

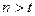Далее выражают уравненные значения превышений в виде функций от определяемых неизвестных 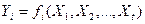и вводят понятие приближённые значения определяемых неизвестных 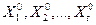; приближённые значения неизвестных можно либо вычислить каким-либо способом, либо принять произвольными, но так, чтобы отличие приближённых и уравненных значений неизвестных различались на малые величины 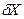. Значения неизвестных представляют в виде суммы 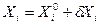и раскладывают функции 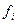в ряд Тейлора относительно поправок 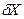, ограничиваясь членами первого порядка малости. Полученные таким образом уравнения называются параметрическим уравнениями поправок

.

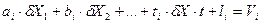В этой формуле буквами 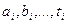обозначены частные производные функции 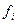по определяемым неизвестным 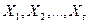. Свободный член 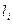получается по формуле 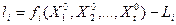. Функция 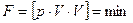представляется в виде

,

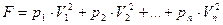и для выполнения условия минимума функции приравнивают нулю 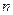её частных производных по .

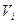На следующем этапе составляют 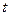нормальных уравнений с 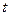параметрами – поправками к приближённым значениям неизвестных. Из решения системы нормальных уравнений (по схеме Гаусса, методом квадратных корней или путём обращения матрицы коэффициентов) находят поправки 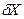к приближённым значениям неизвестных. Далее вычисляют уравненные значения неизвестных 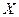, поправки в измерения, уравненные значения измеренных элементов и выполняют оценку точности. При оценке точности вычисляют ошибку единицы веса

Дата добавления: 2014-12-07